【题目】某班共有学生45人，其中女生18人，现用分层抽样的方法，从男、女学生中各抽取若干学生进行演讲比赛，有关数据见下表（单位：人）
性别 | 学生人数 | 抽取人数 |
女生 | 18 |
|
男生 |
| 3 |
（1）求
和
；
（2）若从抽取的学生中再选2人做专题演讲，求这2人都是男生的概率．
科目：高中数学 来源： 题型：
【题目】小王想进行理财投资，根据长期收益率市场顶测，投资A类产品和B类产品的收益分别为
（万元），它们与投资额x（万元）存在如下关系式：
，
，小王准备将200万元资金投入A、B两类理财产品，公司要求每类产品的投资金额不能低于25万元
（1）若对B类产品的投资金额为x（万元），求总收益y（万元）关于x的函数关系式；
（2）请你帮助小王预算如何分配投资资金，才能使总收益最大，并求出最大总收益.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=|ax-2|+lnx（其中a为常数）
（1）若a=0，求函数g（x）=
的极值；
（2）求函数f（x）的单调区间；
（3）令F（x）=f（x）-
，当a≥2时，判断函数F（x）在（0，1]上零点的个数，并说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
，直线
不过原点O且不平行于坐标轴， 
与
有两
个交点A、B，线段AB的中点为M.
（1）若
，点K在椭圆
上， 
、
分别为椭圆的两个焦点，求
的范围；
（2）证明：直线
的斜率与
的斜率的乘积为定值；
（3）若
过点
，射线OM与
交于点P，四边形
能否为平行四边形？
若能，求此时
的斜率；若不能，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
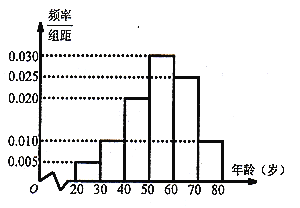
【题目】2018年中央电视台春节联欢晚会分会场之一落户黔东南州黎平县肇兴侗寨，黔东南州某中学高二社会实践小组就社区群众春晚节目的关注度进行了调查，随机抽取80名群众进行调查，将他们的年龄分成6段： 
,
,
,
， 
， 
，得到如图所示的频率分布直方图.
（Ⅰ）求这80名群众年龄的中位数；
（Ⅱ）将频率视为概率，现用随机抽样方法从该社区群众中每次抽取1人，共抽取3次，记被抽取的3人中年龄在
的人数为
，若每次抽取的结果是相互独立的，求
的分布列，及数学期望
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某名校从
年到
年考入清华，北大的人数可以通过以下表格反映出来。（为了方便计算，将年编号为
，
年编为
，以此类推……）
年份 |
|
|
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
|
（1）将这
年的数据分为人数不少于
人和少于人两组，按分层抽样抽取
年，问考入清华、北大的人数不少于20的应抽多少年？在抽取的这年里，若随机的抽取两年恰有一年考入清华、北大的人数不少于的概率是多少？；
（2）根据最近年的数据，利用最小二乘法求出与之间的线性回归方程，并用以预测
年该校考入清华、北大的人数。（结果要求四舍五入至个位）
参考公式：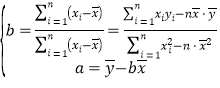
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在标有“甲”的袋中有
个红球和
个白球，这些球除颜色外完全相同．
（Ⅰ）若从袋中依次取出
个球，求在第一次取到红球的条件下，后两次均取到白球的概率；
（Ⅱ）现从甲袋中取出个
红球， 
个白球，装入标有“乙”的空袋．若从甲袋中任取
球，乙袋中任取
球，记取出的红球的个数为
，求
的分布列和数学期望
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
