【题目】如图，在梯形
中，
，
，
，平面
平面，四边形
是菱形，
．
（1）求证：
；
（2）求多面体
被平面分成两部分的体积比．
【答案】（1）证明见解析 （2）1：2
【解析】
（1）根据线段及
，可求得
，由勾股定理逆定理可证明
；由平面与平面垂直的性质可得
，连接CF，由菱形性质可得
，即可得
平面
，因而
.
（2）由点D向线段AC做垂线，垂足为M，则点M为AC中点,可得
平面
，分别求得
和
即可得两部分的体积比.
（1）证明：在等腰梯形
中，由
，，
可得
，
∴
，即，
∵平面
平面，
∴
平面，而
平面，
∴．
连接CF，∵四边形是菱形，
∴，
又
，
∴平面，
∵
平面
，
∴；
（2）∵
，由点D向线段AC做垂线，垂足为M，则点M为AC中点,如下图所示:
∵平面平面，交线为AC，
∴平面，
∴
∵，
∴面，
∴
∴多面体EF﹣ABCD被平面ACEF分成两部分的体积比为1：2．
科目：高中数学 来源： 题型：
【题目】已知偶函数
，当
时，
，当
时，
．关于偶函数
的图象
和直线
的
个命题如下：
①当
时，存在直线
与图象恰有
个公共点；
②若对于
，直线与图象的公共点不超过
个，则
；
③
，
，使得直线与图象交于个点，且相邻点之间的距离相等．
其中正确命题的序号是（ ）．
A. ①②B. ①③C. ②③D. ①②③
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设X～N(μ1，
)，Y～N(μ2，
)，这两个正态分布密度曲线如图所示，下列结论中正确的是 ( )
A. P(Y≥μ2)≥P(Y≥μ1)
B. P(X≤σ2)≤P(X≤σ1)
C. 对任意正数t，P(X≥t)≥P(Y≥t)
D. 对任意正数t，P(X≤t)≥P(Y≤t)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】有甲、乙两个班级进行数学考试，按照大于等于85分为优秀，85分以下为非优秀统计成绩，得到如下所示的列联表：
优秀 | 非优秀 | 总计 | |
甲班 | 10 |
| |
乙班 |
| 30 | |
总计 |
|
已知在全部105人中随机抽取1人，成绩优秀的概率为
，则下列说法正确的是( )
A. 列联表中
的值为30，
的值为35
B. 列联表中的值为15，的值为50
C. 根据列联表中的数据，若按
的可靠性要求，能认为“成绩与班级有关系”
D. 根据列联表中的数据，若按的可靠性要求，不能认为“成绩与班级有关系”
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线
与
轴相交于点
，点
坐标为
，过点作直线
的垂线，交直线于点
．记过、、三点的圆为圆
．
（1）求圆的方程；
（2）求过点与圆相交所得弦长为
的直线方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，以坐标原点
为极点，
轴的正半轴为极轴建立极坐标系，曲线
的方程为
，过点
的直线
的参数方程为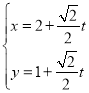
（
为参数）.
（Ⅰ）求直线的普通方程与曲线的直角坐标方程；
（Ⅱ）若直线与曲线交于
、
两点，求
的值，并求定点
到，两点的距离之积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
