
【题目】某次招聘分为笔试和面试两个环节,且只有笔试过关者方可进入面试环节,笔试与面试都过关才会被录用.笔试需考完全部三科,且至少有两科优秀才算笔试过关,面试需考完全部两科且两科均为优秀才算面试过关.假设某考生笔试三科每科优秀的概率均为![]() ,面试两科每科优秀的概率均为
,面试两科每科优秀的概率均为![]() .
.
(1)求该考生被录用的概率;
(2)设该考生在此次招聘活动中考试的科目总数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某大学生参加社会实践活动,对某公司1月份至6月份销售某种配件的销售量及销售单价进行了调查,销售单价![]() 和销售量
和销售量![]() 之间的一组数据如下表所示:
之间的一组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量 | 11 | 10 | 8 | 6 | 5 | 14.2 |
(1)根据1至5月份的数据,先求出![]() 关于
关于![]() 的回归直线方程;6月份的数据作为检验数据.若由回归直线方程得到的预测数据与检验数据的误差不超过
的回归直线方程;6月份的数据作为检验数据.若由回归直线方程得到的预测数据与检验数据的误差不超过![]() ,则认为所得到的回归直线方程是理想的.试问所求得的回归直线方程是否理想?
,则认为所得到的回归直线方程是理想的.试问所求得的回归直线方程是否理想?
(2)预计在今后的销售中,销售量与销售单价仍然服从(1)中的回归关系,如果该种机器配件的成本是![]() 元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
参考数据:![]() ,
,![]() .
.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: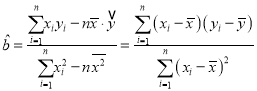 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为![]() 的正方体
的正方体![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上任意一点,
上任意一点,![]() ,
,![]() 为
为![]() 上任意两点,且
上任意两点,且![]() 的长为定值,则下面的四个值中不为定值的是( )
的长为定值,则下面的四个值中不为定值的是( )
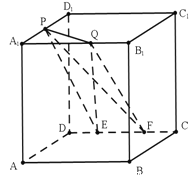
A. 点![]() 到平面
到平面![]() 的距离B. 三棱锥
的距离B. 三棱锥![]() 的体积
的体积
C. 直线![]() 与平面
与平面![]() 所成的角D. 二面角
所成的角D. 二面角![]() 的大小
的大小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如下表:

(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若近几年该农产品每千克的价格![]() (单位:元)与年产量
(单位:元)与年产量![]() 满足的函数关系式为
满足的函数关系式为![]() ,且每年该农产品都能售完.
,且每年该农产品都能售完.
①根据(1)中所建立的回归方程预测该地区![]() 年该农产品的产量;
年该农产品的产量;
②当![]() 为何值时,销售额
为何值时,销售额![]() 最大?
最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: 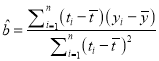 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂共有![]() 名工人,已知这
名工人,已知这![]() 名工人去年完成的产品数都在区间
名工人去年完成的产品数都在区间![]() (单位:万件)内,其中每年完成
(单位:万件)内,其中每年完成![]() 万件及以上的工人为优秀员工,现将其分成
万件及以上的工人为优秀员工,现将其分成![]() 组,第
组,第![]() 组、第
组、第![]() 组、第
组、第![]() 组、第
组、第![]() 组、第
组、第![]() 组对应的区间分别为
组对应的区间分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并绘制出如图所示的频率分布直方图.
,并绘制出如图所示的频率分布直方图.
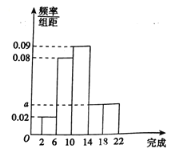
(1)求![]() 的值,并求去年优秀员工人数;
的值,并求去年优秀员工人数;
(2)选取合适的抽样方法从这![]() 名工人中抽取容量为
名工人中抽取容量为![]() 的样本,求这
的样本,求这![]() 组分别应抽取的人数;
组分别应抽取的人数;
(3)现从(2)中![]() 人的样本中的优秀员工中随机选取
人的样本中的优秀员工中随机选取![]() 名传授经验,求选取的
名传授经验,求选取的![]() 名工人在同一组的概率.
名工人在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,且曲线
轴的正半轴为极轴建立极坐标系,且曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 上的定点
上的定点![]() 在曲线
在曲线![]() 外且其到
外且其到![]() 上的点的最短距离为
上的点的最短距离为![]() ,试求点
,试求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年4月1日,新华通讯社发布:国务院决定设立河北雄安新区.消息一出,河北省雄县、容城、安新3县及周边部分区域迅速成为海内外高度关注的焦点.
(1)为了响应国家号召,北京市某高校立即在所属的8个学院的教职员工中作了“是否愿意将学校整体搬迁至雄安新区”的问卷调查,8个学院的调查人数及统计数据如下:
调查人数( | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
愿意整体搬迁人数( | 8 | 17 | 25 | 31 | 39 | 47 | 55 | 66 |
请根据上表提供的数据,用最小二乘法求出变量![]() 关于变量
关于变量![]() 的线性回归方程
的线性回归方程![]() 保留小数点后两位有效数字);若该校共有教职员工2500人,请预测该校愿意将学校整体搬迁至雄安新区的人数;
保留小数点后两位有效数字);若该校共有教职员工2500人,请预测该校愿意将学校整体搬迁至雄安新区的人数;
(2)若该校的8位院长中有5位院长愿意将学校整体搬迁至雄安新区,现该校拟在这8位院长中随机选取4位院长组成考察团赴雄安新区进行实地考察,记![]() 为考察团中愿意将学校整体搬迁至雄安新区的院长人数,求
为考察团中愿意将学校整体搬迁至雄安新区的院长人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式及数据:  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,短轴的一个端点到焦点的距离为
,短轴的一个端点到焦点的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() 的中点在直线
的中点在直线![]() 上,求直线
上,求直线![]() 与
与![]() 轴交点纵坐标的最小值.
轴交点纵坐标的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com