
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,两个焦点与短轴一个顶点构成等腰直角三角形,过点
,两个焦点与短轴一个顶点构成等腰直角三角形,过点![]() 且与x轴不重合的直线l与椭圆交于M,N不同的两点.
且与x轴不重合的直线l与椭圆交于M,N不同的两点.
(Ⅰ)求椭圆P的方程;
(Ⅱ)当AM与MN垂直时,求AM的长;
(Ⅲ)若过点P且平行于AM的直线交直线![]() 于点Q,求证:直线NQ恒过定点.
于点Q,求证:直线NQ恒过定点.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)由题意布列关于a,b的方程组,即可得到结果;
(2)由![]() 与
与![]() 垂直得
垂直得![]() ,结合点在曲线上,可得M点坐标,结合两点间距离公式可得结果;
,结合点在曲线上,可得M点坐标,结合两点间距离公式可得结果;
(3)设![]() ,
,![]() ,由题意,设直线
,由题意,设直线![]() 的方程为
的方程为![]() ,利用韦达定理即可得到结果.
,利用韦达定理即可得到结果.
(1)因为![]() ,所以
,所以![]()
因为两个焦点与短轴一个顶点构成等腰直角三角形,
所以![]() ,
,
又![]() ,
,
所以![]() ,
,
所以椭圆方程为![]() .
.
(2)方法一:
设![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
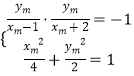 ,
,
![]() ,
,![]() (舍)
(舍)
所以![]() .
.
方法二:
设![]() ,
,
因为![]() 与
与![]() 垂直,
垂直,
所以点![]() 在以
在以![]() 为直径的圆上,
为直径的圆上,
又以![]() 为直径的圆的圆心为
为直径的圆的圆心为![]() ,半径为
,半径为![]() ,方程为
,方程为![]() ,
,
 ,
,
![]() ,
,![]() (舍)
(舍)
所以![]()
方法三:
设直线![]() 的斜率为
的斜率为![]() ,
,![]() ,其中
,其中 ![]()
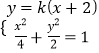
化简得![]()
当![]() 时,
时,![]()
得![]() ,
,![]()
显然直线![]() 存在斜率且斜率不为0.
存在斜率且斜率不为0.
因为![]() 与
与![]() 垂直,
垂直,
所以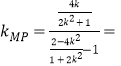
![]() ,
,
得![]() ,
,![]() ,
, ![]() ,
,
所以![]()
(3)直线![]() 恒过定点
恒过定点![]() ,
,
设![]() ,
,![]() ,
,
由题意,设直线![]() 的方程为
的方程为![]() ,
,
由 ![]() 得
得![]() ,
,
显然,![]() ,则
,则![]() ,
,![]() ,
,
因为直线![]() 与
与![]() 平行,所以
平行,所以![]() ,
,
则![]() 的直线方程为
的直线方程为![]() ,
,
令![]() ,则
,则![]() ,即
,即![]() ,
,
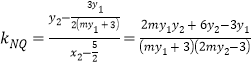 ,
,
直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,
,
因为![]() ,故
,故![]() ,
,
所以直线![]() 恒过定点
恒过定点![]() .
.


科目:高中数学 来源: 题型:
【题目】在![]() 中,角
中,角![]() ,
, ![]() ,
, ![]() 所对的边分别为
所对的边分别为![]() ,
, ![]() ,
, ![]() ,且
,且![]() .
.
(Ⅰ)求角![]() 的大小;
的大小;
(Ⅱ)已知![]() ,
, ![]() 的面积为
的面积为![]() ,求
,求![]() 的周长.
的周长.
【答案】(Ⅰ)![]() .(Ⅱ)
.(Ⅱ)![]() .
.
【解析】【试题分析】(I)利用正弦定理和三角形内角和定理化简已知,可求得![]() 的值,进而求得
的值,进而求得![]() 的大小.(II)利用余弦定理和三角形的面积公式列方程组求解的
的大小.(II)利用余弦定理和三角形的面积公式列方程组求解的![]() 的值,进而求得三角形周长.
的值,进而求得三角形周长.
【试题解析】
(Ⅰ)由![]() 及正弦定理得,
及正弦定理得, ![]() ,
,
![]()
![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() .
.
又∵![]() ,∴
,∴![]() .
.
(Ⅱ)由![]() ,
, ![]() ,根据余弦定理得
,根据余弦定理得![]() ,
,
由![]() 的面积为
的面积为![]() ,得
,得![]() .
.
所以![]()
![]() ,得
,得![]() ,
,
所以![]() 周长
周长![]() .
.
【题型】解答题
【结束】
18
【题目】为促进农业发展,加快农村建设,某地政府扶持兴建了一批“超级蔬菜大棚”.为了解大棚的面积与年利润之间的关系,随机抽取了其中的7个大棚,并对当年的利润进行统计整理后得到了如下数据对比表:
大棚面积(亩) | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 |
年利润(万元) | 6 | 7 | 7.4 | 8.1 | 8.9 | 9.6 | 11.1 |
由所给数据的散点图可以看出,各样本点都分布在一条直线附近,并且![]() 与
与![]() 有很强的线性相关关系.
有很强的线性相关关系.
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)小明家的“超级蔬菜大棚”面积为8.0亩,估计小明家的大棚当年的利润为多少;
(Ⅲ)另外调查了近5年的不同蔬菜亩平均利润(单位:万元),其中无丝豆为:1.5,1.7,2.1,2.2,2.5;彩椒为:1.8,1.9,1.9,2.2,2.2,请分析种植哪种蔬菜比较好?
参考数据: ![]() ,
, ![]() .
.
参考公式:  ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() ,
,![]() .有下列命题:
.有下列命题:
①对![]() ,恒有
,恒有![]() 成立.
成立.
②![]() ,使得
,使得![]() 成立.
成立.
③“若![]() ,则有
,则有![]() 且
且![]() .”的否命题.
.”的否命题.
④“若![]() 且
且![]() ,则有
,则有![]() .”的逆否命题.
.”的逆否命题.
其中,真命题有_____________.(只需填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
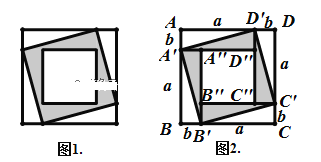
【题目】下图1,是某设计员为一种商品设计的平面logo样式.主体是由内而外的三个正方形构成.该图的设计构思如图2,中间正方形![]() 的四个顶点,分别在最外围正方形ABCD的边上,且分所在边为a,b两段.设中间阴影部分的面积为
的四个顶点,分别在最外围正方形ABCD的边上,且分所在边为a,b两段.设中间阴影部分的面积为![]() ,最内正方形
,最内正方形![]() 的面积为
的面积为![]() .当
.当![]() ,且
,且![]() 取最大值时,定型该logo的最终样式,则此时a,b的取值分别为_____________.
取最大值时,定型该logo的最终样式,则此时a,b的取值分别为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的公差
的公差![]() ,数列
,数列![]() 满足
满足![]() ,集合
,集合![]() .
.
(1)若![]() ,求集合
,求集合![]() ;
;
(2)若![]() ,求
,求![]() 使得集合
使得集合![]() 恰好有两个元素;
恰好有两个元素;
(3)若集合![]() 恰好有三个元素:
恰好有三个元素:![]() ,
,![]() 是不超过7的正整数,求
是不超过7的正整数,求![]() 的所有可能的值.
的所有可能的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com