
【题目】设三棱锥![]() 的每个顶点都在球
的每个顶点都在球![]() 的球面上,
的球面上,![]() 是面积为
是面积为![]() 的等边三角形,
的等边三角形,![]() ,
,![]() ,且平面
,且平面![]() 平面
平面![]() .
.
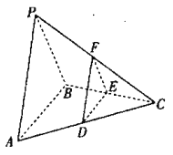
(1)确定![]() 的位置(需要说明理由),并证明:平面
的位置(需要说明理由),并证明:平面![]() 平面
平面![]() .
.
(2)与侧面![]() 平行的平面
平行的平面![]() 与棱
与棱![]() ,
,![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() ,
,![]() ,求四面体
,求四面体![]() 的体积的最大值.
的体积的最大值.
【答案】(1)![]() 在
在![]() 上,理由见解析,证明见解析,(2)
上,理由见解析,证明见解析,(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,可证
,可证![]() 在线段
在线段![]() 上,
上,![]() 且
且![]() 平面
平面![]() ,从而得到平面
,从而得到平面![]() 平面
平面![]() .
.
(2)设![]() ,可证
,可证![]() ,利用导数可求体积的最大值.
,利用导数可求体积的最大值.
(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,取点
,取点![]() 为
为![]() 的三等分点且
的三等分点且![]() ,
,
连接![]() .
.
因为![]() ,所以
,所以![]() .
.
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,故
,故![]() .
.
因为![]() 为等腰直角三角形,
为等腰直角三角形,![]() 为
为![]() 的中点,故
的中点,故![]() ,
,
因为![]() ,
,![]() ,
,
故![]() ,故
,故![]() ,同理
,同理![]() ,
,
因为![]() 是等边三角形,故
是等边三角形,故![]() 为
为![]() 的中心,故
的中心,故![]() ,
,
故![]() 为三棱锥
为三棱锥![]() 的外接球的球心,
的外接球的球心,
故![]() 与
与![]() 重合即
重合即![]() 在线段
在线段![]() 上且
上且![]() .
.

因为![]() 在
在![]() 上,所以
上,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)由题意得![]() ,解得
,解得![]() ,
,
因为![]() 为等腰直角三角形,
为等腰直角三角形,![]() 为
为![]() 的中点,故
的中点,故![]() ,
,
而平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() ,故
,故![]() 为点
为点![]() 到平面
到平面![]() 的距离.
的距离.
在等腰直角三角形![]() 中,
中,![]() 即
即![]() 到平面
到平面![]() 的距离
的距离![]() .
.
设![]() ,
,![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
故![]() ,同理
,同理![]() ,因为
,因为![]() 方向相同,故
方向相同,故![]() ,
,
同理![]() ,
,
所以![]() ,则
,则![]() 的面积为
的面积为![]() .
.
又![]() ,所以
,所以![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
所以四面体![]() 的体积
的体积![]() .
.
设![]() ,
,![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 为增函数,在
为增函数,在![]() 为减函数,
为减函数,
所以![]() ,
,
即四面体![]() 的体积的最大值为
的体积的最大值为![]() .
.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
【题目】随着经济全球化、信息化的发展,企业之间的竞争从资源的争夺转向人才的竞争,吸引、留住培养和用好人才成为人力资源管理的战略目标和紧迫任务,在此背景下,某信息网站在15个城市中对刚毕业的大学生的月平均收入薪资和月平均期望薪资做了调查,数据如下图所示.
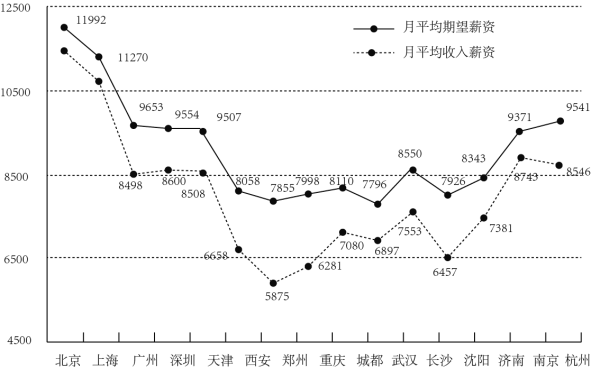
(1)若某大学毕业生从这15座城市中随机选择一座城市就业,求该生选中月平均收入薪资高于8500元的城市的概率;
(2)现有2名大学毕业生在这15座城市中各随机选择一座城市就业,且2人的选择相互独立,记X为选中月平均收入薪资高于8500元的城市的人数,求X的分布列和数学期望E(X);
(3)记图中月平均收入薪资对应数据的方差为![]() ,月平均期望薪资对应数据的方差为
,月平均期望薪资对应数据的方差为![]() ,判断
,判断![]() 与
与![]() 的大小(只需写出结论)
的大小(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图三棱锥A-BCD中,BD⊥CD,E,F分别为棱BC,CD上的点,且BD∥平面AEF,AE⊥平面BCD.
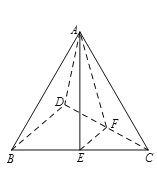
(1)求证:平面AEF⊥平面ACD;
(2)若![]() ,
,![]() 为
为![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与抛物线
与抛物线![]() :
:![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 的面积为16(
的面积为16(![]() 为坐标原点).
为坐标原点).
(1)求![]() 的方程;
的方程;
(2)直线![]() 经过
经过![]() 的焦点
的焦点![]() 且
且![]() 不与
不与![]() 轴垂直,与
轴垂直,与![]() 交于
交于![]() ,
,![]() 两点,若线段
两点,若线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,证明:
,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在椭圆![]() 上任取一点
上任取一点![]() (
(![]() 不为长轴端点),连结
不为长轴端点),连结![]() 、
、![]() ,并延长与椭圆
,并延长与椭圆![]() 分别交于点
分别交于点![]() 、
、![]() 两点,已知
两点,已知![]() 的周长为8,
的周长为8,![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设坐标原点为![]() ,当
,当![]() 不是椭圆的顶点时,直线
不是椭圆的顶点时,直线![]() 和直线
和直线![]() 的斜率之积是否为定值?若是定值,请求出这个定值;若不是定值,请说明理由.
的斜率之积是否为定值?若是定值,请求出这个定值;若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() 为等腰直角三角形,
为等腰直角三角形,![]() 为等边三角形,其中O为BC中点,且
为等边三角形,其中O为BC中点,且![]() .
.
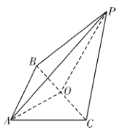
(1)求证:平面![]() 平面PBC;
平面PBC;
(2)若![]() 且
且![]() 平面EBC,其中E为AP上的点,求CE与平面ABC所成角的正弦值.
平面EBC,其中E为AP上的点,求CE与平面ABC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 、
、![]() 与平面
与平面![]() 、
、![]() 满足
满足![]() ,
,![]() ,
,![]() ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A.![]() 是
是![]() 的充分不必要条件
的充分不必要条件
B.![]() 是
是![]() 的充要条件
的充要条件
C.设![]() ,则
,则![]() 是
是![]() 的必要不充分条件
的必要不充分条件
D.设![]() ,则
,则![]() 是
是![]() 的既不充分也不必要条件
的既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com