
【题目】为了让税收政策更好的为社会发展服务,国家在修订《中华人民共和国个人所得税法》之后,发布了《个人所得税专项附加扣除暂行办法》,明确“专项附加扣除”就是子女教育、继续教育大病医疗、住房贷款利息、住房租金赠养老人等费用,并公布了相应的定额扣除标准,决定自2019年1月1日起施行,某机关为了调查内部职员对新个税方案的满意程度与年龄的关系,通过问卷调查,整理数据得如下2×2列联表:
40岁及以下 | 40岁以上 | 合计 | |
基本满意 | 15 | 10 | 25 |
很满意 | 25 | 30 | 55 |
合计 | 40 | 40 | 80 |
(1)根据列联表,能否有85%的把握认为满意程度与年龄有关?
(2)若已经在满意程度为“基本满意”的职员中用分层抽样的方式选取了5名职员,现从这5名职员中随机选取3名进行面谈求面谈的职员中恰有2名年龄在40岁及以下的概率.
附:![]() ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)没有85%的把握(2)![]()
【解析】
(1)根据列联表可以求得K2的观测值,结合临界值表可得;(2)由题意,在满意程度为“基本满意“的职员中用分层抽样的方式选取5名职员,应抽取40岁以下和40岁以上分别为3名和2名,记为A,B,C,d,e,然后用列举法列举出随机选3名的基本事件和面谈的职员中恰有2名年龄在40岁及以下的基本事件,然后用古典概型的概率公式可得.
(1)根据列联表可以求得![]() 的观测值:
的观测值:
![]() .
.
∵![]() .
.
∴没有85%的把握认为满意程度与年龄有关.
(2)由题意,在满意程度“基本满意”的职员中用分层抽样的方式选取5名职员,应抽取40岁及以下和40岁以上分别为3名和2名,记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
则随机选3名,基本事件为:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共10个.
,共10个.
满足题意的基本事件为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共6个.
,共6个.
设从这5名职员中随机选取3名进行面谈,面谈的职员中恰有2名年龄在40岁及以下的概率为![]() .则
.则![]() .
.


科目:高中数学 来源: 题型:
【题目】给出四个命题:①若x2﹣3x+2=0,则x=1或x=2;②若x=y=0,则x2+y2=0;③已知x,y∈N,若x+y是奇数,则x、y中一个是奇数,一个是偶数;④若x1,x2是方程x2﹣2![]() x+2=0的两根,则x1,x2可以是一椭圆与一双曲线的离心率,那么( )
x+2=0的两根,则x1,x2可以是一椭圆与一双曲线的离心率,那么( )
A.③的否命题为假B.①的逆否命题为假
C.②的逆命题为真D.④的逆否命题为假
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足x2﹣4ax+3a2<0(a>0),命题q:实数x满足x2﹣5x+6<0.
(1)若a=1,且p∧q为真命题,求实数x的取值范围;
(2)若p是q的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构对A市居民手机内安装的“APP”(英文Application的缩写,一般指手机软件)的个数和用途进行调研,在使用智能手机的居民中随机抽取了100人,获得了他们手机内安装APP的个数,整理得到如图所示频率分布直方图:
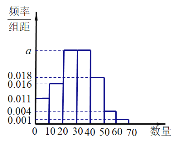
(Ⅰ)从A市随机抽取一名使用智能手机的居民,试估计该居民手机内安装APP的个数不低于30的概率;
(Ⅱ)从A市随机抽取3名使用智能手机的居民进一步做调研,用X表示这3人中手机内安装APP的个数在[20,40)的人数.
①求随机变量X的分布列及数学期望;
②用Y1表示这3人中安装APP个数低于20的人数,用Y2表示这3人中手机内安装APP的个数不低于40的人数.试比较EY1和EY2的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是两条异面直线,直线
是两条异面直线,直线![]() 与
与![]() 都垂直,则下列说法正确的是( )
都垂直,则下列说法正确的是( )
A. 若![]() 平面
平面![]() ,则
,则![]()
B. 若![]() 平面
平面![]() ,则
,则![]() ,
,![]()
C. 存在平面![]() ,使得
,使得![]() ,
,![]() ,
,![]()
D. 存在平面![]() ,使得
,使得![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆:![]() 的四个顶点围成的四边形的面积为
的四个顶点围成的四边形的面积为![]() ,原点到直线
,原点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知定点![]() ,是否存在过
,是否存在过![]() 的直线
的直线![]() ,使
,使![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 的左顶点?若存在,求出
的左顶点?若存在,求出![]() 的方程:若不存在,请说明理由.
的方程:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物),为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5浓度的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量x(万辆) | 100 | 102 | 108 | 114 | 116 |
PM2.5的浓度y(微克/立方米) | 78 | 80 | 84 | 88 | 90 |
(1)根据上表数据,用最小二乘法,求出y关于x的线性回归方程![]() x
x![]() ;
;
(2)若周六同一时间段车流量200万辆,试根据(1)求出的线性回归方程,预测此时PM2.5的浓度为多少?
(参考公式: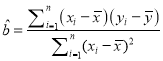 ,
,![]()
![]() ;参考数据:
;参考数据:![]() xi=540,
xi=540,![]() yi=420)
yi=420)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】六棱锥![]() 中,底面
中,底面![]() 是正六边形,
是正六边形,![]() 底面
底面![]() ,给出下列四个命题:
,给出下列四个命题:
①线段![]() 的长是点
的长是点![]() 到线段
到线段![]() 的距离;
的距离;
②异面直线![]() 与
与![]() 所成角是
所成角是![]() ;
;
③线段![]() 的长是直线
的长是直线![]() 与平面
与平面![]() 的距离;
的距离;
④![]() 是二面角
是二面角![]() 平面角.
平面角.
其中所有真命题的序号是_______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (t为参数),以坐标原点
(t为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,圆
轴正半轴为极轴,建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)过曲线![]() 上任一点
上任一点![]() 作与
作与![]() 夹角为45°的直线,交
夹角为45°的直线,交![]() 于点
于点![]() ,求
,求![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com