
����Ŀ����ֽ�����ҹ��Ŵ��Ĵ���֮һ��ֽ�ŵĹ����ָֽ���Ƴɺ��������бߣ��ó�һ���ijߴ�.�����ҹ����ù��ʱ����涨��![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ������
������![]() �ȱ������ʾֽ�ŵķ�����.��ӡֽ������ֻ����
�ȱ������ʾֽ�ŵķ�����.��ӡֽ������ֻ����![]() ϵ�к�
ϵ�к�![]() ϵ�У�����
ϵ�У�����![]() ϵ�еķ�����Ϊ����
ϵ�еķ�����Ϊ����![]() ����ֽ�ŵķ���(��
����ֽ�ŵķ���(��![]() ��ʾ)�ͳ���(��
��ʾ)�ͳ���(��![]() ��ʾ)�ı�����ϵΪ
��ʾ)�ı�����ϵΪ![]() ���ڽ�
���ڽ�![]() ֽ���س��ȷ���Կ������ȷ֣����Ϊ
ֽ���س��ȷ���Կ������ȷ֣����Ϊ![]() ���
���![]() ֽ���س��ȷ���Կ������ȷ֣����Ϊ
ֽ���س��ȷ���Կ������ȷ֣����Ϊ![]() ���������˶Կ���
���������˶Կ���![]() ���.����
���.����![]() ��
��![]() ��
��![]() ������
������![]() ֽ��һ��.��
ֽ��һ��.��![]() ֽ�����Ϊ
ֽ�����Ϊ![]() .����9��ֽ�����֮�͵���__________
.����9��ֽ�����֮�͵���__________![]() ��
��
 ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д� �����ܾ�ϵ�д�
�����ܾ�ϵ�д� ���ƿ�����ϵ�д�
���ƿ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ��ֱ��l��y��kx��1���㣬���PΪֱ��l�ϵĶ��㣬��P��������C���������ߣ�A��BΪ�е㣮
��ֱ��l��y��kx��1���㣬���PΪֱ��l�ϵĶ��㣬��P��������C���������ߣ�A��BΪ�е㣮
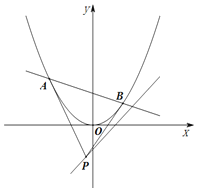
��1��֤����ֱ��AB�������Q��
��2��������PAB�������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵxOy�У�����C�IJ�������Ϊ![]() ��
��![]() Ϊ��������ֱ��l�IJ�������Ϊ
Ϊ��������ֱ��l�IJ�������Ϊ![]() ��tΪ����������������ԭ��Ϊ���㣬x��������Ϊ����ļ�����ϵ�У�����m��
��tΪ����������������ԭ��Ϊ���㣬x��������Ϊ����ļ�����ϵ�У�����m��![]() ��
��
��1����C��l�ļ����귽�̣�
��2����m��C��l�ֱ�������ԭ���A��B���㣬��![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Բ����![]() ����ѧ��չʷ�ϳ��ֹ������д���������������շ�ʵ��Ͳ���˹ʵ�飮��������������Ҳ����ͨ����������ʵ��������
����ѧ��չʷ�ϳ��ֹ������д���������������շ�ʵ��Ͳ���˹ʵ�飮��������������Ҳ����ͨ����������ʵ��������![]() ��ֵ������120��ͬѧÿ�����д��һ��x��y��С��1����ʵ����
��ֵ������120��ͬѧÿ�����д��һ��x��y��С��1����ʵ����![]() ����ͳ������x��y����1���ɶ۽����������ߵ�����
����ͳ������x��y����1���ɶ۽����������ߵ�����![]() �ĸ���m��������ͳ�Ƹ���m����
�ĸ���m��������ͳ�Ƹ���m����![]() ��ֵ�����ͳ�ƽ����
��ֵ�����ͳ�ƽ����![]() ����ô���Թ���
����ô���Թ���![]() ��ֵΪ�� ��
��ֵΪ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��߲�Ʒ������ij��ҵ�����������ž��������ڵس���Ʒ���м�⣬����ij���������������ȡ100����Ʒ����������ݵĶԱȣ�����ÿ����Ʒ�����ۺ����֣�����100�֣�����ÿ����Ʒ���õ��ۺ������Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.���ۺ�����Ϊ80�ּ����ϵIJ�ƷΪһ��Ʒ.
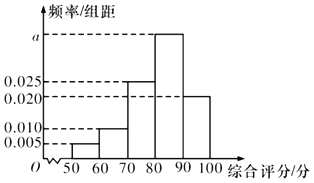
��1����ͼ��![]() ��ֵ�������ۺ����ֵ���λ����
��ֵ�������ۺ����ֵ���λ����
��2���������������壬��Ƶ����Ϊ���ʣ����ֲ������˼�룬���ڸ����������������ȡ5����Ʒ���ٴ���5����Ʒ�������ȡ2����Ʒ��¼�й����ݣ�����2����Ʒ��ǡ��һ��һ��Ʒ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ��Ϊ�˺������ǵ������̶ȣ���ϣ������ѧ��ϲ��ǡ˹(![]() ����������)�ڹ�Ԫǰ����������������ǵ��������.�ǵȵ���ֵԽС�����Ǿ�Խ�����ǵȵ���ֵԽ�����Ĺ��Խ��.����1850�꣬���ڹ�ȼ��������Ȳ����е�Ӧ�ã�Ӣ������ѧ����ɭ(
����������)�ڹ�Ԫǰ����������������ǵ��������.�ǵȵ���ֵԽС�����Ǿ�Խ�����ǵȵ���ֵԽ�����Ĺ��Խ��.����1850�꣬���ڹ�ȼ��������Ȳ����е�Ӧ�ã�Ӣ������ѧ����ɭ(![]() )������˺������������̶ȵ����ȵĸ���.����������̶ȿ������ǵȻ�����������.�����ǵ��ǵ�����������
)������˺������������̶ȵ����ȵĸ���.����������̶ȿ������ǵȻ�����������.�����ǵ��ǵ�����������![]() .�����ǵ�Ϊ
.�����ǵ�Ϊ![]() ���ǵ�����Ϊ
���ǵ�����Ϊ![]() .��֪�����������ǵ���1.00.��������� ���ǵ���1.25.���������������������������
.��֪�����������ǵ���1.00.��������� ���ǵ���1.25.���������������������������![]() ��������
��������![]() ��ӽ�����(��
��ӽ�����(��![]() ��Сʱ��
��Сʱ�� ![]() )
)
A.1.24B.1.25C.1.26D.1.27
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ������
������![]() ��������
��������![]() ������
������![]() Ϊ���㡢
Ϊ���㡢![]() ��ķǸ�����Ϊ����ļ�����ϵ����������ϵȡ��ͬ�ĵ�λ���ȣ��У�����
��ķǸ�����Ϊ����ļ�����ϵ����������ϵȡ��ͬ�ĵ�λ���ȣ��У�����![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ����ֱ��
����ֱ��![]() ��������
��������![]() ����������
����������![]() ����
����![]() ��
��![]() ���㣮
���㣮
�������![]() ��ֱ�����꼰����
��ֱ�����꼰����![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
������֤������![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() Ϊ��ֵ��
Ϊ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����Բ![]() ��������Ϊ
��������Ϊ![]() ����
����![]() ������
������![]() ��һ��ֱ�߽���Բ��
��һ��ֱ�߽���Բ��![]() ��
��![]() ���㣬���߶�
���㣬���߶�![]() ���е�
���е�![]() ��
��![]() �Ĵ��߽�
�Ĵ��߽�![]() ���ڵ�
���ڵ�![]() .
.
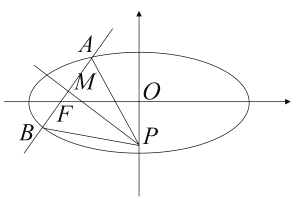
��1������Բ���̣�
��2����![]() ������ʱ����ֱ��
������ʱ����ֱ��![]() ��б��.
���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ![]() �У�����
�У�����![]() �IJ�������Ϊ
�IJ�������Ϊ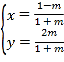 ��
��![]() Ϊ��������������ԭ��
Ϊ��������������ԭ��![]() Ϊ���㣬
Ϊ���㣬![]() ��ķǸ�����Ϊ���Ὠ��������ϵ������
��ķǸ�����Ϊ���Ὠ��������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��
��
��1��������![]() ����ͨ���̺�
����ͨ���̺�![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��2������![]() ����б��Ϊ
����б��Ϊ![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() ���㣬��
���㣬��![]() ����
����![]() ƽ�е�ֱ��
ƽ�е�ֱ��![]() ��
��![]() ��
��![]() �㣬��
�㣬��![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com