
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (
(![]() 为参数),直线l的参数方程为
为参数),直线l的参数方程为![]() (t为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,射线m:
(t为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,射线m:![]() .
.
(1)求C和l的极坐标方程;
(2)设m与C和l分别交于异于原点的A,B两点,求![]() 的最大值.
的最大值.
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】数列![]() ,
,![]() ,
,![]() 满足:
满足:![]() ,
,![]() ,
,![]() .
.
(1)若数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等差数列;
是等差数列;
(2)若数列![]() ,
,![]() 都是等差数列,求证:数列
都是等差数列,求证:数列![]() 从第二项起为等差数列;
从第二项起为等差数列;
(3)若数列![]() 是等差数列,试判断当
是等差数列,试判断当![]() 时,数列
时,数列![]() 是否成等差数列?证明你的结论.
是否成等差数列?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新闻出版业不断推进供给侧结构性改革,深入推动优化升级和融合发展,持续提高优质出口产品供给,实现了行业的良性发展.下面是2012年至2016年我国新闻出版业和数字出版业营收增长情况,则下列说法错误的是( )
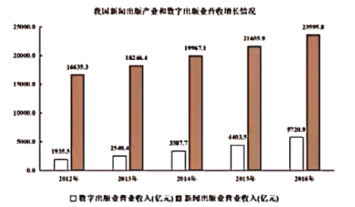
A. 2012年至2016年我国新闻出版业和数字出版业营收均逐年增加
B. 2016年我国数字出版业营收超过2012年我国数字出版业营收的2倍
C. 2016年我国新闻出版业营收超过2012年我国新闻出版业营收的1.5倍
D. 2016年我国数字出版营收占新闻出版营收的比例未超过三分之一
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某班学生喜爱打篮球是否与性别有关,对该班40名学生进行了问卷调查,得到了如下的![]() 列联表:
列联表:
男生 | 女生 | 总计 | |
喜爱打篮球 | 19 | 15 | 34 |
不喜爱打篮球 | 1 | 5 | 6 |
总计 | 20 | 20 | 40 |
(1)在女生的20个个体中,随机抽取2人,记随机变量![]() 为抽到“不喜爱篮球”的人数,求
为抽到“不喜爱篮球”的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(2)判断能否在犯错误的概率不超过0.1的条件下认为喜爱篮球与性别有关?
附: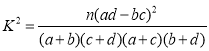 ,其中
,其中![]() .
.
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】造纸术是我国古代四大发明之一,纸张的规格是指纸张制成后,经过修整切边,裁成一定的尺寸.现在我国采用国际标准,规定以![]() 、
、![]() 、…、
、…、![]() ;
;![]() 、
、![]() 、…、
、…、![]() 等标记来表示纸张的幅面规格.复印纸幅面规格只采用
等标记来表示纸张的幅面规格.复印纸幅面规格只采用![]() 系列和
系列和![]() 系列,共中
系列,共中![]() 系列的幅面规格为:①
系列的幅面规格为:①![]() 规格的纸张的幅宽(以
规格的纸张的幅宽(以![]() 表示)和长度(以
表示)和长度(以![]() 表示)的比例关系为
表示)的比例关系为![]() ;②将
;②将![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格,
规格,![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格,…,如此对开至
规格,…,如此对开至![]() 规格.现有
规格.现有![]() 、
、![]() 、
、![]() 、…、
、…、![]() 纸各一张.若
纸各一张.若![]() 纸的面积为
纸的面积为![]() .则这9张纸的面积之和等于__________
.则这9张纸的面积之和等于__________![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着国家综合国力的提升和科技的进步,截至![]() 年底,中国铁路运营里程达
年底,中国铁路运营里程达![]() 万千米,这个数字比
万千米,这个数字比![]() 年增长了
年增长了![]() 倍;高铁运营里程突破
倍;高铁运营里程突破![]() 万千米,占世界高铁运营里程的
万千米,占世界高铁运营里程的![]() 以上,居世界第一位.如表截取了
以上,居世界第一位.如表截取了![]() 年中国高铁密度的发展情况(单位:千米/万平方千米).
年中国高铁密度的发展情况(单位:千米/万平方千米).
年份 |
|
|
|
|
|
年份代码 |
|
|
|
|
|
高铁密度 |
|
|
|
|
|
已知高铁密度![]() 与年份代码
与年份代码![]() 之间满足关系式
之间满足关系式![]() (
(![]() 为大于
为大于![]() 的常数).
的常数).
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程(精确到
的回归方程(精确到![]() 位);
位);
(2)利用(1)的结论,预测到哪一年,高铁密度会超过![]() 千米/万平方千米.
千米/万平方千米.
参考公式:设具有线性相关系的两个变量![]() 的一组数据为
的一组数据为![]() ,则回归方程
,则回归方程![]() 的系数:
的系数: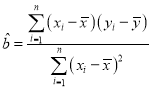 ,
,![]()
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com