
【题目】已知函数![]() .
.
(1)讨论函数![]() 的极值;
的极值;
(2)是否存在实数![]() ,使得不等式
,使得不等式![]() 在
在![]() 上恒成立?若存在,求出
上恒成立?若存在,求出![]() 的最小值:若不存在,请说明理由.
的最小值:若不存在,请说明理由.
【答案】(1)答案不唯一,具体见解析(2)存在;![]() 的最小值是1
的最小值是1
【解析】
(1)对![]() (或
(或![]() )是否恒成立分类讨论,若恒成立,没有极值点,若不恒成立,求出
)是否恒成立分类讨论,若恒成立,没有极值点,若不恒成立,求出![]() 的解,即可求出结论;
的解,即可求出结论;
(2)令![]() ,可证
,可证![]() 恒成立,而
恒成立,而![]() ,由(2)得,
,由(2)得,![]() 在
在![]() 为减函数,
为减函数,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 都存在
都存在![]() ,不满足
,不满足![]() ,当
,当![]() 时,设
时,设![]() ,且
,且![]() ,只需求出
,只需求出![]() 在
在![]() 单调递增时
单调递增时![]() 的取值范围即可.
的取值范围即可.
(1)由题知,![]() ,
,
①当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递减,没有极值;
上单调递减,没有极值;
②当![]() 时,令
时,令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() 单调递增,
单调递增,
故![]() 在
在![]() 处取得极小值
处取得极小值![]() ,无极大值.
,无极大值.
(2)不妨令![]() ,
,
设![]() 在
在![]() 恒成立,
恒成立,
![]() 在
在![]() 单调递增,
单调递增,![]() ,
,
![]() 在
在![]() 恒成立,
恒成立,
所以当![]() 时,
时,![]() ,
,
由(1)知,当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
![]() 恒成立;
恒成立;
所以若要不等式![]() 在
在![]() 上恒成立,只能
上恒成立,只能![]() .
.
当![]() 时,
时,![]() ,由(1)知,
,由(1)知,![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,不满足题意.
,不满足题意.
当![]() 时,设
时,设![]() ,
,
因为![]() ,所以
,所以![]() ,
,
![]()
![]() ,
,
所以![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,
所以当![]() 时,
时,![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
故存在![]() ,使得不等式
,使得不等式![]() 在
在![]() 上恒成立.
上恒成立.
此时![]() 的最小值是1.
的最小值是1.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某校从学生会宣传部6名成员(其中男生4人,女生2人)中,任选3人参加某省举办的“我看中国改革开放三十年”演讲比赛活动.
(1)设所选3人中女生人数为ξ,求ξ的分布列;
(2)求男生甲或女生乙被选中的概率;
(3)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(B)和P(B|A).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,上、下顶点分别是
,上、下顶点分别是![]() 、
、![]() ,上、下焦点分别是
,上、下焦点分别是![]() 、
、![]() ,焦距为
,焦距为![]() ,点
,点![]() 在椭圆上.
在椭圆上.
(1)求椭圆的方程;
(2)若![]() 为椭圆上异于
为椭圆上异于![]() 、
、![]() 的动点,过
的动点,过![]() 作与
作与![]() 轴平行的直线
轴平行的直线![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,判断
,判断![]() 是否为定值,说明理由.
是否为定值,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从数列![]() 中取出部分项组成的数列称为数列
中取出部分项组成的数列称为数列![]() 的“子数列”.
的“子数列”.
(1)若等差数列![]() 的公差
的公差![]() ,其子数列
,其子数列![]() 恰为等比数列,其中
恰为等比数列,其中![]() ,
,![]() ,
,![]() ,求
,求![]() ;
;
(2)若![]() ,
,![]() ,判断数列
,判断数列![]() 是否为
是否为![]() 的“子数列”,并证明你的结论.
的“子数列”,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设复数β=x+yi(x,y∈R)与复平面上点P(x,y)对应.
(1)若β是关于t的一元二次方程t2﹣2t+m=0(m∈R)的一个虚根,且|β|=2,求实数m的值;
(2)设复数β满足条件|β+3|+(﹣1)n|β﹣3|=3a+(﹣1)na(其中n∈N*、常数![]() ),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点
),当n为奇数时,动点P(x、y)的轨迹为C1.当n为偶数时,动点P(x、y)的轨迹为C2.且两条曲线都经过点![]() ,求轨迹C1与C2的方程;
,求轨迹C1与C2的方程;
(3)在(2)的条件下,轨迹C2上存在点A,使点A与点B(x0,0)(x0>0)的最小距离不小于![]() ,求实数x0的取值范围.
,求实数x0的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某工厂生产的某种产品中抽取1000件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
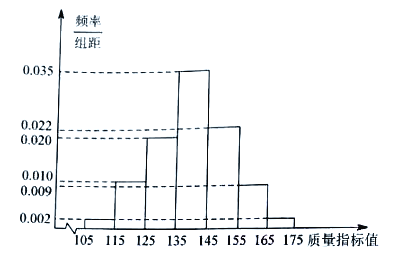
(1)求这1000件产品质量指标值的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表)
(同一组数据用该区间的中点值作代表)
(2)由频率分布直方图可以认为,这种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,其中以
,其中以![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(ⅰ)利用该正态分布,求![]() ;
;
(ⅱ)某用户从该工厂购买了100件这种产品,记![]() 表示这100件产品中质量指标值为于区间(127.6,140)的产品件数,利用(ⅰ)的结果,求
表示这100件产品中质量指标值为于区间(127.6,140)的产品件数,利用(ⅰ)的结果,求![]() .
.
附:![]() .若
.若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线x=﹣2上有一动点Q,过点Q作直线l,垂直于y轴,动点P在l1上,且满足![]() (O为坐标原点),记点P的轨迹为C.
(O为坐标原点),记点P的轨迹为C.
(1)求曲线C的方程;
(2)已知定点M(![]() ,0),N(
,0),N(![]() ,0),点A为曲线C上一点,直线AM交曲线C于另一点B,且点A在线段MB上,直线AN交曲线C于另一点D,求△MBD的内切圆半径r的取值范围.
,0),点A为曲线C上一点,直线AM交曲线C于另一点B,且点A在线段MB上,直线AN交曲线C于另一点D,求△MBD的内切圆半径r的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com