
【题目】历史上有不少数学家都对圆周率作过研究,第一个用科学方法寻求圆周率数值的人是阿基米德,他用圆内接和外切正多边形的周长确定圆周长的上下界,开创了圆周率计算的几何方法,而中国数学家刘徽只用圆内接正多边形就求得![]() 的近似值,他的方法被后人称为割圆术.近代无穷乘积式、无穷连分数、无穷级数等各种
的近似值,他的方法被后人称为割圆术.近代无穷乘积式、无穷连分数、无穷级数等各种![]() 值的表达式纷纷出现,使得
值的表达式纷纷出现,使得![]() 值的计算精度也迅速增加.华理斯在1655年求出一个公式:
值的计算精度也迅速增加.华理斯在1655年求出一个公式:![]() ,根据该公式绘制出了估计圆周率
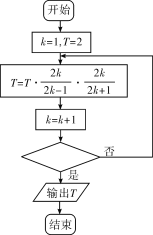
,根据该公式绘制出了估计圆周率![]() 的近似值的程序框图,如下图所示,执行该程序框图,已知输出的
的近似值的程序框图,如下图所示,执行该程序框图,已知输出的![]() ,若判断框内填入的条件为
,若判断框内填入的条件为![]() ,则正整数
,则正整数![]() 的最小值是
的最小值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知圆C方程为![]() ,椭圆中心在原点,焦点在x轴上.
,椭圆中心在原点,焦点在x轴上.
(1)证明圆C恒过一定点M,并求此定点M的坐标;
(2)判断直线![]() 与圆C的位置关系,并证明你的结论;
与圆C的位置关系,并证明你的结论;
(3)当![]() 时,圆C与椭圆的左准线相切,且椭圆过(1)中的点M,求此时椭圆方程;在x轴上是否存在两定点A,B使得对椭圆上任意一点Q(异于长轴端点),直线
时,圆C与椭圆的左准线相切,且椭圆过(1)中的点M,求此时椭圆方程;在x轴上是否存在两定点A,B使得对椭圆上任意一点Q(异于长轴端点),直线![]() ,
,![]() 的斜率之积为定值?若存在,求出A,B坐标;若不存在,请说明理由.
的斜率之积为定值?若存在,求出A,B坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在![]() 上任意一点
上任意一点![]() 处的切线
处的切线![]() 为
为![]() ,若过右焦点
,若过右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,已知在点
两点,已知在点![]() 处切线相交于
处切线相交于![]() .
.
(Ⅰ)求![]() 点的轨迹方程;
点的轨迹方程;
(Ⅱ)①若过点![]() 且与直线
且与直线![]() 垂直的直线(斜率存在且不为零)交椭圆
垂直的直线(斜率存在且不为零)交椭圆![]() 于
于![]() 两点,证明
两点,证明![]() 为定值.
为定值.
②四边形![]() 的面积是否有最小值,若有请求出最小值;若没有请说明理由.
的面积是否有最小值,若有请求出最小值;若没有请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业质量检验员为了检测生产线上零件的情况,从生产线上随机抽取了![]() 个零件进行测量,根据所测量的零件尺寸(单位:mm),得到如下的频率分布直方图:
个零件进行测量,根据所测量的零件尺寸(单位:mm),得到如下的频率分布直方图:
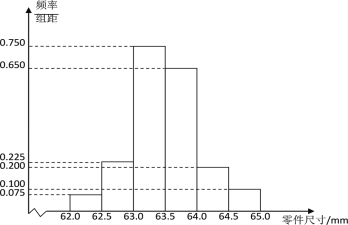
(1)根据频率分布直方图,求这![]() 个零件尺寸的中位数(结果精确到
个零件尺寸的中位数(结果精确到![]() );
);
(2)已知尺寸在![]() 上的零件为一等品,否则为二等品. 将这
上的零件为一等品,否则为二等品. 将这![]() 个零件尺寸的样本频率视为概率,从生产线上随机抽取
个零件尺寸的样本频率视为概率,从生产线上随机抽取![]() 个零件,试估计所抽取的零件是二等品的概率.
个零件,试估计所抽取的零件是二等品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,直线![]() 将矩形纸
将矩形纸![]() 分为两个直角梯形
分为两个直角梯形![]() 和
和![]() ,将梯形
,将梯形![]() 沿边
沿边![]() 翻折,如图2,在翻折的过程中(平面
翻折,如图2,在翻折的过程中(平面![]() 和平面
和平面![]() 不重合),下面说法正确的是
不重合),下面说法正确的是
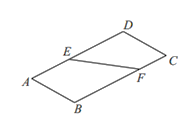
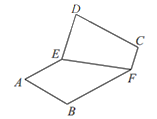
图1 图2
A.存在某一位置,使得![]() 平面
平面![]()
B.存在某一位置,使得![]() 平面
平面![]()
C.在翻折的过程中,![]() 平面
平面![]() 恒成立
恒成立
D.在翻折的过程中,![]() 平面
平面![]() 恒成立
恒成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆E:![]() +
+![]() =1(a>b>0)的左、右焦点分别为F1,F2,过点F1的直线交椭圆E于A,B两点.若椭圆E的离心率为
=1(a>b>0)的左、右焦点分别为F1,F2,过点F1的直线交椭圆E于A,B两点.若椭圆E的离心率为![]() ,三角形ABF2的周长为4
,三角形ABF2的周长为4![]() .
.
(1)求椭圆E的方程;
(2)设不经过椭圆的中心而平行于弦AB的直线交椭圆E于点C,D,设弦AB,CD的中点分别为M,N,证明:O,M,N三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() 3,g(x)=alnx﹣2x(a∈R).
3,g(x)=alnx﹣2x(a∈R).
(1)讨论g(x)的单调性;
(2)是否存在实数a,使不等式f(x)≥g(x)恒成立?如果存在,求出a的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年寒假是特殊的寒假,因为疫情全体学生只能在家进行网上在线学习,为研究学生网上学习的情况,某校社团对男女各10名学生进行了网上在线学习的问卷调查,每名学生给出评分(满分100分),得到如图所示的茎叶图.
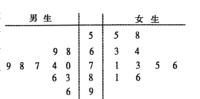
(1)根据茎叶图判断男生组和女生组哪个组对网课的评价更高?并说明理由;
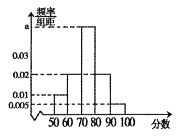
(2)如图是按该20名学生的评分绘制的频率分布直方图,求![]() 的值并估计这20名学生评分的平均值(同一组中的数据用该组区间中点值作为代表);
的值并估计这20名学生评分的平均值(同一组中的数据用该组区间中点值作为代表);
(3)求该20名学生评分的中位数![]() ,并将评分超过
,并将评分超过![]() 和不超过
和不超过![]() 的学生数填入下面的列联表:
的学生数填入下面的列联表:
超过 | 不超过 | |
男生 | ||
女生 |
根据列联表,能否有![]() 的把握认为男生和女生的评分有差异?
的把握认为男生和女生的评分有差异?
附: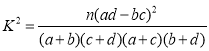 ,
,
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com