
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,倾斜角为
,倾斜角为![]() 的直线
的直线![]() 过点
过点![]() 与拋物线
与拋物线![]() 交于
交于![]() 两点,
两点, ![]() 为坐标原点,
为坐标原点, ![]() 的面积为
的面积为![]() .
.
(1)求![]() ;
;
(2)设点![]() 为直线
为直线![]() 与拋物线
与拋物线![]() 在第一象限的交点,过点
在第一象限的交点,过点![]() 作
作![]() 的斜率分别为
的斜率分别为![]() 的两条弦
的两条弦![]() ,如果
,如果![]() ,证明直线
,证明直线![]() 过定点,并求出定点坐标.
过定点,并求出定点坐标.
【答案】(1)![]() ;(2)直线
;(2)直线![]() 经过定点
经过定点![]() .
.
【解析】试题分析:
(1)焦点坐标![]() ,联立直线方程与抛物线方程得
,联立直线方程与抛物线方程得![]() .
.
结合韦达定理和面积公式得到关于实数p的方程: ![]() ,
,
解得![]() .
.
(2)很明显![]() 都不等于零.设直线
都不等于零.设直线![]() ,与抛物线方程联立,结合韦达定理可得直线方程为
,与抛物线方程联立,结合韦达定理可得直线方程为![]() ,则直线
,则直线![]() 经过定点
经过定点![]() .
.
试题解析:
(1)![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,代入抛物线方程得
,代入抛物线方程得![]() .
.
设![]() ,则
,则![]() .
.
根据抛物线定义![]() ,所以
,所以![]() .
.
坐标原点![]() 到直线
到直线![]() 的距离
的距离 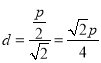 .
.
所以![]() 的面积为
的面积为![]() ,解得
,解得![]() .
.
(2)抛物线方程为![]() ,直线
,直线![]() ,即
,即![]() ,解得
,解得![]() .
.
设![]() .根据题意,显然
.根据题意,显然![]() 都不等于零.
都不等于零.
直线![]() ,即
,即![]() ,代入抛物线方程得
,代入抛物线方程得![]() .
.
由于点![]() 在抛物线上,依据根与系数的关系得
在抛物线上,依据根与系数的关系得![]() ,所以
,所以![]() . 同理
. 同理![]() .
.
而直线![]() 的方程为
的方程为![]() ,因为
,因为![]() 也抛物线上,所以
也抛物线上,所以![]() 代入上述方程并整理得
代入上述方程并整理得![]() ,
,
![]() ,
,
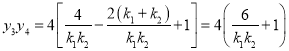 .
.
令![]() ,则
,则![]() ,代入
,代入![]() 的方程得
的方程得![]() ,
,
整理得![]() ,
,
若上式对任意变化的![]() 恒成立,则
恒成立,则![]() ,解得
,解得![]()
故直线![]() 经过定点
经过定点![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正数,其前n项的和为Sn , 且对任意的m,n∈N*,
都有(Sm+n+S1)2=4a2ma2n .
(1)求 ![]() 的值;
的值;
(2)求证:{an}为等比数列;
(3)已知数列{cn},{dn}满足|cn|=|dn|=an , p(p≥3)是给定的正整数,数列{cn},{dn}的前p项的和分别为Tp , Rp , 且Tp=Rp , 求证:对任意正整数k(1≤k≤p),ck=dk .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(1)证明:PB∥平面AEC;
(2)设AP=1,AD= ![]() ,三棱锥P﹣ABD的体积V=
,三棱锥P﹣ABD的体积V= ![]() ,求A到平面PBC的距离.
,求A到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知长方体ABCD﹣A1B1C1D1中,E,M,N分别是BC,AE,CD1的中点,AD=AA1=a,AB=2a.求证:MN∥平面ADD1A1 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:y=kx﹣1与双曲线x2﹣y2=1的左支交于A,B两点.
(1)求斜率k的取值范围;
(2)若直线l2经过点P(﹣2,0)及线段AB的中点Q且l2在y轴上截距为﹣16,求直线l1的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以椭圆的一个短轴端点及两个焦点构成的三角形的面积为
,以椭圆的一个短轴端点及两个焦点构成的三角形的面积为![]() ,圆C方程为
,圆C方程为![]() .
.
(1)求椭圆及圆C的方程;
(2)过原点O作直线l与圆C交于A,B两点,若![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图茎叶图记录了甲、乙两组各四名同学的植树棵树.乙组记录中有一个数据模糊,无法确认,在图中以X表示.
(注:方差 ![]() ,其中
,其中 ![]() 为x1 , x2 , …xn的平均数)
为x1 , x2 , …xn的平均数)
(1)如果X=8,求乙组同学植树棵树的平均数和方差;
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com