
全 国 大 调 研
数学试题(一)
注:1.本卷总分150分,考试时间120分钟;
2. 考试范围:高考考试大纲规定的考试内容。

第Ⅰ卷(选择题 共60分)
一、
选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.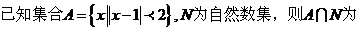

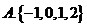
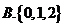
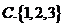

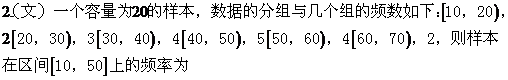


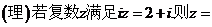

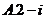
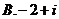
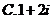
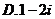


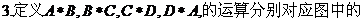 ①②③④,那么图中的⑤⑥所对应的运算结果可能是
①②③④,那么图中的⑤⑥所对应的运算结果可能是





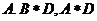
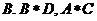

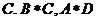
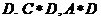

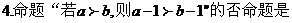

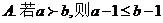
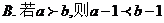

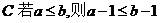
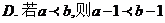



A. 1
B
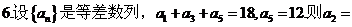

A. 2
B
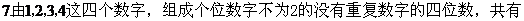

A 8个 B.9个
C.18个 D.19个
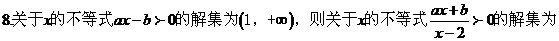

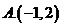
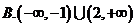

C.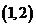
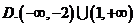

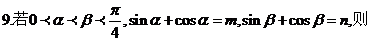

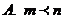
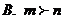
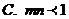
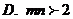


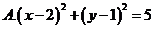
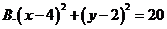

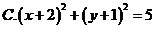
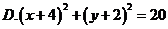

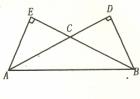
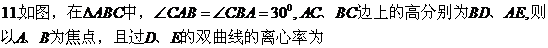

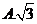

 D.2
D.2
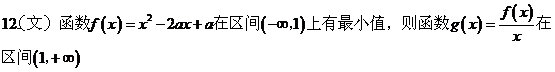 A. 有最小值
B. 有最大值 C. 是减函数
D. 是增函数
A. 有最小值
B. 有最大值 C. 是减函数
D. 是增函数
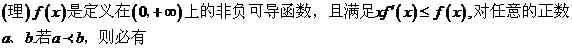
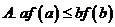
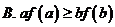

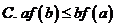
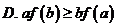


题号
1
2
3
4
5
6
7
8
9
10
11
12
答案


第Ⅱ卷(非选择题 共90分)
二、
填空题:本大题共4小题,每小题5分,共20分,把答案填在题中横线上。


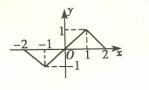
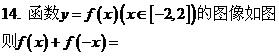

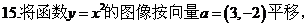

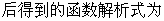

16.下列两个命题,是否需要在“ ”上加一个条件或结论才能构成真命?如果需要,请填写出一个相应的条件;如果不需要,则在“ ”上划“/”
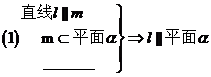

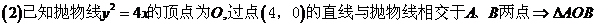
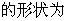


三、
解答题:本大题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分10分)
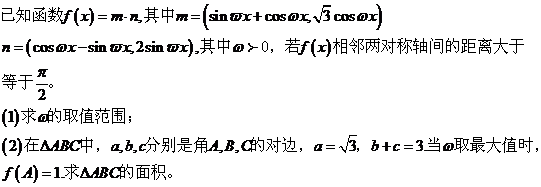



18. (本小题满分12分)
北京时间
(1)
若再让两人各自射击3次,张娟娟与朴成贤各恰好两次击中9环的概率哪个大(结果以分数的形式表示)?
(2)
若在让两人各自射击3次,求朴成贤每次都击中9环以上的概率(结果一分数的形式表示)
(理)(3)设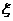 为张娟娟在这次决赛中击中的环数,求
为张娟娟在这次决赛中击中的环数,求 的期望。
的期望。







19. (本小题满分12分)
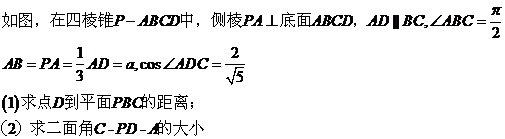









20. (本小题满分12分)
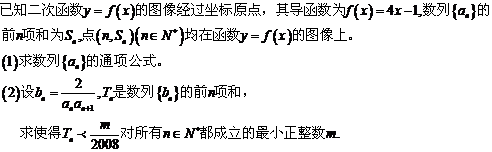





21. (本小题满分12分)
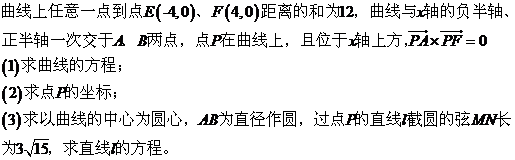









22. (本小题满分12分)
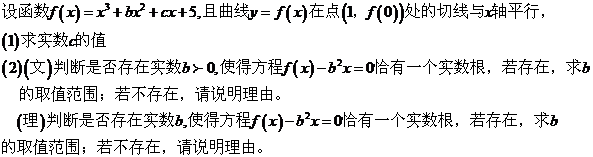
调研(一)数学答案
1.B
2.(文)B 样本在区间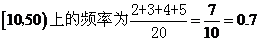
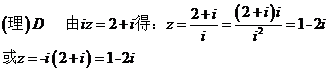
3.B
4.C
5.B 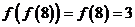
6.C. 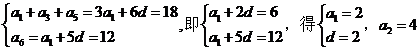
7.C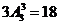
8.B.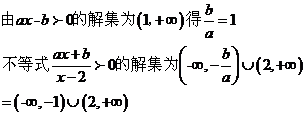
9.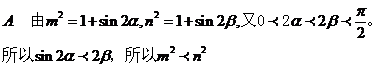
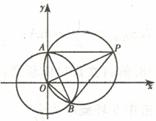 10.A
如图,
10.A
如图,
圆心在OP中点(2,1),
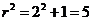 ,
,
即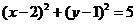 ,
,
11.C 设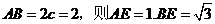 ,
,
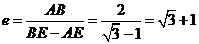 。
。
12.(文)D 由函数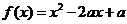 在区间
在区间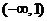 上有最小值,则
上有最小值,则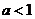 ,
,
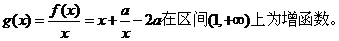
(理) 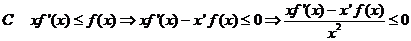 ,
,
令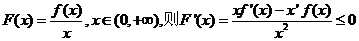 ,
,
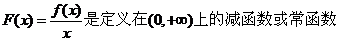 ,
,
又正数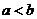 ,则必有
,则必有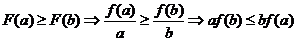 ,
,
13.20
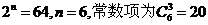 。
。
14.0
15.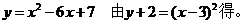
16.(1)
17.解: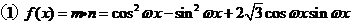
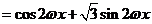
 ,…………………………………………………………3分
,…………………………………………………………3分
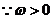 ,
,
 ,
,
由题意可知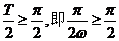 ,
,
解得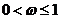 ,
,
即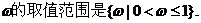 ……………………………………5分
……………………………………5分
(2)由(1)可知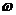 的最大值为1,
的最大值为1,
 ,
,
 ,
,
而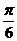
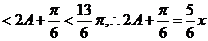 ,
,
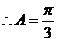 …………………………………………………………8分
…………………………………………………………8分
由余弦定理知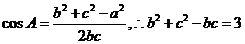 ,
,
又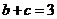 ,联立解得
,联立解得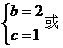
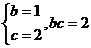 ,
,
18.解:(文)(1)依题意:张娟娟射击一次,击中10环的概率为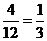 ,
,
击中9环概率为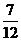 ,
,
所以射击三次恰好两次击中9环的概率为: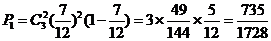 ,
,
同理,补成贤恰好两次击中9环的概率为: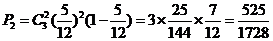 ,
,
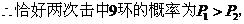
张娟娟击中9环的概率较大; ........................6分
(2)朴成贤每次都击中9环以上的概率;
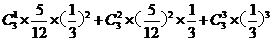
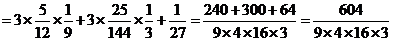
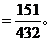
朴成贤每次都击中9环以上的概率为 ...............文12分 理10分
...............文12分 理10分
(理)(3)
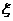
10
9
8
7
P
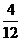
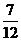
0
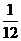
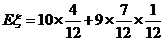
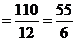 ………………………………………………………………12分
………………………………………………………………12分
19.解法一:(1)如图,在四棱锥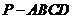 中,
中,
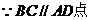
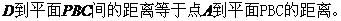
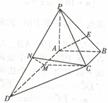
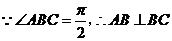 ,
,
又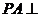 低面
低面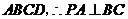 ,
,
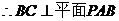 ,………………………………………3分
,………………………………………3分
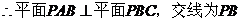 ,
,
过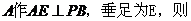
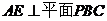 ,
,
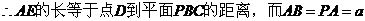 ,
,
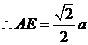 ,
,
即点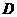 到平面
到平面 …………………………………………6分
…………………………………………6分
(2)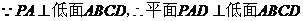
引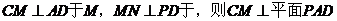 ,
,
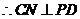 ,
,
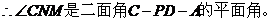 ………………………………9分
………………………………9分

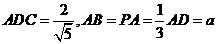 ,
,
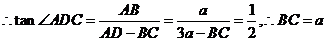 ,
,
可知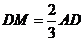 ,
,
又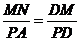 ,
,
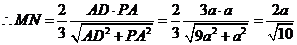 ,
,
 ,
,
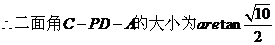 ………………………………12分
………………………………12分
解法二:如图,A为原点,分别以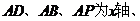
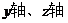 ,建立空间直=角坐标系。
,建立空间直=角坐标系。
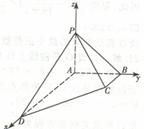 (1)
(1)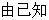
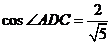 ,
,
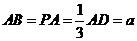 ,
,
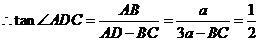 ,
,
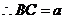
则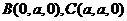 ,
,
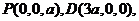 ……………………………………4分
……………………………………4分
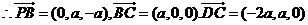 ,
,
设平面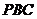 的一个法向量为
的一个法向量为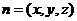 ,
,
则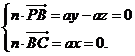 令
令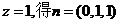 ,
,
则点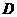 到平面
到平面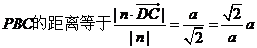 ,…………………7分
,…………………7分
(2)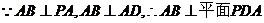 ,
,
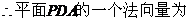
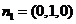 ,
,
设平面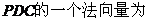
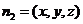 ,
,
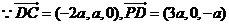 ,
,
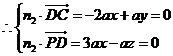
令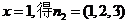 ,…………………………………………10分
,…………………………………………10分
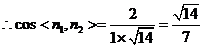 ,
,

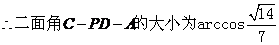 …………………………12分
…………………………12分
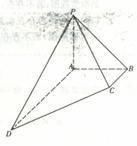
20.解:(1)已知二次函数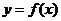 的图像经过坐标原点,
的图像经过坐标原点,
设这三次函数为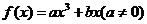 ,
,
则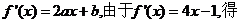
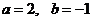 ,
,
所以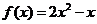 ,…………………………………………3分
,…………………………………………3分
又因为点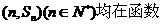
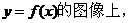
所以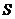
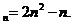
当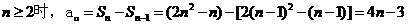 ,
,
当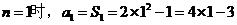 ,
,
所以,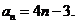 ……………………………………6分
……………………………………6分
(2)由(1)得知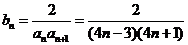
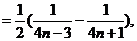 …………………………………………9分
…………………………………………9分
故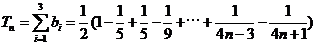
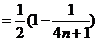 ,
,
因此,要使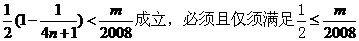 ,
,
即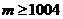 ,
,
所以满足要求的最小正整数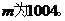 ……………………………12分
……………………………12分
21.解:(1)设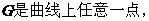
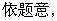
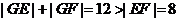 ,
,
所以曲线是以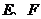 为焦点的椭圆,
为焦点的椭圆,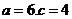 ,
,
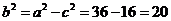 ,
,
所以所求的椭圆方程为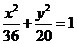 ;……………………………………………3分
;……………………………………………3分
(2)由已知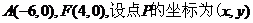 ,
,
则
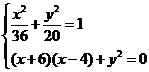
则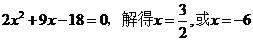 ,
,
由于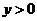 ,所以只能取
,所以只能取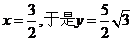 ,
,
所以点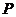 的坐标为(
的坐标为(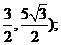 ……………………………………6分
……………………………………6分
(3)圆心为(0,0),半径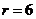
圆方程为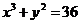 ,
,
若过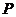 的直线
的直线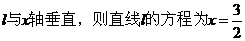 ,
,
这时,圆心到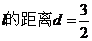 ,
,
所以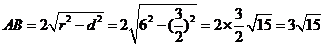 ,
,
符合题意;……………………………………9分
若过
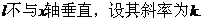
则直线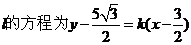 ,
,
即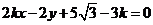 ,
,
这时,圆心到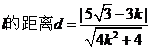 ,
,
所以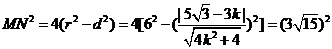 ,
,
化简得,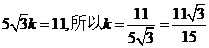 ,
,
所以直线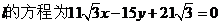 ,
,
综上,所求的直线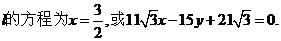 ……12分
……12分
22.解:(1)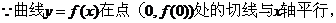
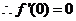
又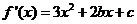 ,
,
则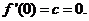 ..............3分
..............3分
(2)(文)由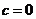 ,方程
,方程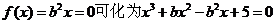 ,
,
假设存在实数 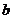 使得此方程恰有一个实数根,
使得此方程恰有一个实数根,
则令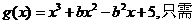
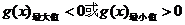 ,
,
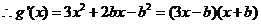 ,............6分
,............6分
令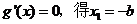 ,
,
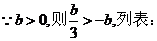
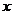
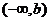
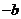
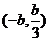
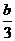
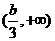
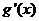
+
0
―
0
+
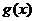
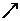
极大值
极小值
……………………………………………………………………9分
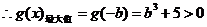
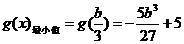 ,
,
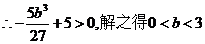 ,
,
实数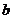 的取值范围是(0,3)。……………………………………………12分
的取值范围是(0,3)。……………………………………………12分
(理)由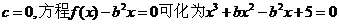 ,
,
假设存在实数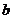 使得此方程恰有一个实数根,
使得此方程恰有一个实数根,
则令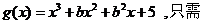
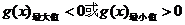 ,
,
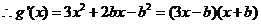 ,………………………5分
,………………………5分
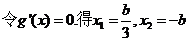 ,
,
①若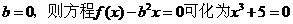 ,
,
此方程恰有一个实根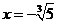 ,
,
②若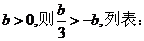
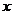
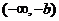
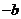
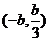
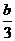
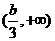
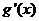
+
0
―
0
+
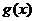
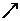
极大值
极小值
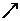

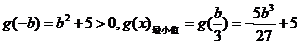 ,
,
 …………………………………9分
…………………………………9分
③若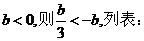
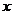
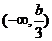
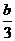

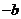
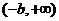
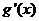
+
0
―
0
+
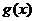
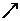
极大值
极小值
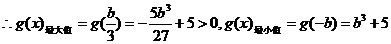 ,
,
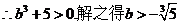 ,
,
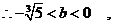
综合①②③可得,实数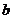 的取值范围是
的取值范围是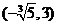 。………………12分
。………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com