
湖北省黄冈中学2007届高三年级结业考试
数 学 试 题(理)
第Ⅰ卷(选择题,共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若实数x, a, 2x, b依次成等差数列,当b≠0时,则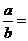
A.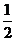 B.
B.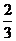 C.
C.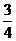 D.
D.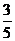
2.已知函数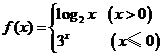 ;则
;则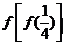 的值是
的值是
A.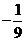 B.
B.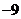 C.
C. D.9
D.9
3.已知a, b∈R,且ab>0,则下列不等式不正确的是
A.|a+b|≥a-b B.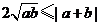
C.|a+b|<|a|+|b| D.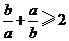
4.有3种不同的树苗需要种植在一条直道的一侧,相邻的两棵树不能是同一种树苗,若第一棵种下是甲种树苗,那么第5棵树又恰好是甲种树苗的种法共有
A.6种 B.9种 C.12种 D.15种
5.已知集合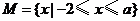 是非空集合,集合
是非空集合,集合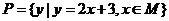 ,集合
,集合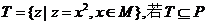 ,则实数a的取值范围是
,则实数a的取值范围是
A.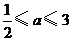 B.
B.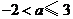 C.
C.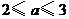 D.
D.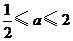
6.已知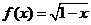 ,当
,当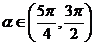 时,式子
时,式子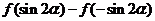 可以化简为
可以化简为
A.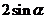 B.
B.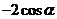 C.
C.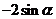 D.
D.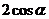
7.给出下列命题,则其中的真命题是( )
A.若直线m、n都平行于平面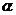 ,则m、n一定不是相交直线
,则m、n一定不是相交直线
B.已知平面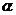 、
、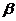 互相垂直,且直线m、n也互相垂直,若
互相垂直,且直线m、n也互相垂直,若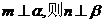
C.直线m、n在平面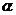 内的射影分别是一个点和一条直线,且
内的射影分别是一个点和一条直线,且 ,则
,则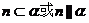
D.直线m、n是异面直线,若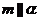 ,则n必与
,则n必与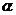 相交
相交
8.设双曲线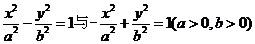 的离心率分别为
的离心率分别为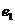 、
、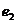 ,则当a、b在变化时,
,则当a、b在变化时,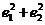 的最小值是( )
的最小值是( )
A.2 B. C.
C.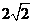 D.4
D.4
9.设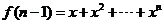 ,且f(x)的展开式中所有项的系数和为An,则
,且f(x)的展开式中所有项的系数和为An,则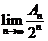 的值为
的值为
A.2 B.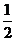 C.
C.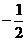 D.
D.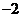
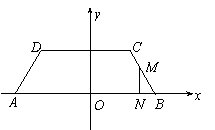 10.如图所示,ABCD为梯形,
10.如图所示,ABCD为梯形,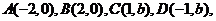 折线EADCBF为某随机变量
折线EADCBF为某随机变量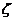 的总体密度曲线,则
的总体密度曲线,则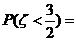
A.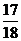 B.
B.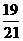
C.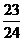 D.
D.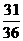
第Ⅱ卷(非选择题,共100分)
二、填空题:本大题共5小题,每小题5分,共25分. 把答案填在答题卡的相应位置上.
11.已知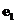 、
、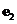 是两个不共线的向量,而
是两个不共线的向量,而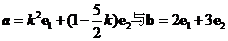 是两个共线向量,则实数k=______________________.
是两个共线向量,则实数k=______________________.
12.在等比数列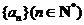 中,Sn为其前n项和,若an>0, a2=4, S4-a1=28,则
中,Sn为其前n项和,若an>0, a2=4, S4-a1=28,则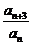 的值为______________.
的值为______________.
13.两条平行直线分别过点A(6,2)和B(-3,-1),各自绕A、B旋转,若这两条平行线距离取最大值时,两直线的方程分别为_________________________________.
14.设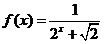 ,用类似推导等差数列前n项求和公式的方法,可求得
,用类似推导等差数列前n项求和公式的方法,可求得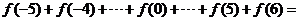 ________________________.
________________________.
15.不等式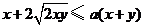 对于一切正数x, y成立,则正数a的最小值是__________.
对于一切正数x, y成立,则正数a的最小值是__________.
答 题 卡
题号
1
2
3
4
5
6
7
8
9
10
答案
题号
11
12
13
14
15
答案
三、解答题:本大题共6小题,共75分. 解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)
已知直线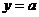 与奇函数
与奇函数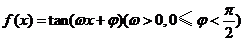 的两个相邻交点间的距离是
的两个相邻交点间的距离是 ,且
,且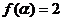 ,求
,求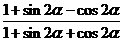 的值.
的值.
17.(本小题满分12分)
如图,菱形ABCD的边长为 平面ABCD,SA=SC=b=6, SB=SD=c=4.
平面ABCD,SA=SC=b=6, SB=SD=c=4.
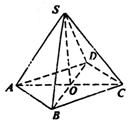 (1)求
(1)求
(2)求SC与AD所成的角.
18.(本小题满分12分)
排球比赛的规则是5局3胜制,已知每局比赛中甲、乙两队获胜的概率分别为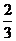 、
、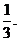
(1)若前两局中乙队以2∶0领先,求最后甲、乙队各自获胜的概率;
(2)乙队以3∶2获胜的概率.
19.(本小题满分12分)
已知二次函数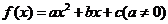 和一次函数
和一次函数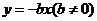 ,其中a、b、c满足条件a>b>c,且a+b+c=0;
,其中a、b、c满足条件a>b>c,且a+b+c=0;
(1)证明:一次函数与二次函数的图象必有两个不同交点A、B;
(2)求线段AB在x轴上的射影A1B1的长的取值范围.
20.(本小题满分13分)
已知数列{an}为等差数列,a1=2,且该数列的前10项和为65,若正数列{bn}满足条件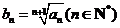 .
.
(1)求数列{bn}的通项公式;
(2)求数列{bn}的最大项;
(3)令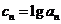 ,判断在数列{cn}中是否存在某连续的三项或三项以上的项,按原来的排列顺序得到的数列是等比数列?为什么?
,判断在数列{cn}中是否存在某连续的三项或三项以上的项,按原来的排列顺序得到的数列是等比数列?为什么?
21.(本小题满分14分)
直线l与抛物线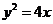 交于两点A、B,O为坐标原点,且
交于两点A、B,O为坐标原点,且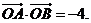
(1)求证:直线l恒过一定点;
(2)若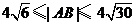 ,求直线l的斜率k的取值范围;
,求直线l的斜率k的取值范围;
(3)设抛物线的焦点为F,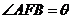 ,试问
,试问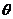 角能否等于120°?若能,求出相应的直线l的方程;若不能,请说明理由.
角能否等于120°?若能,求出相应的直线l的方程;若不能,请说明理由.
1.D 2.C 3.C 4.A 5.A 6.D 7.C 8.D 9.A 10.C
11.  12.
8 13.
12.
8 13.  14.
14.  15. 2
15. 2
16.依题意,即 ,由函数为奇函数,
,由函数为奇函数,
∴对于定义域内的任意x有 ,即
,即
∴ ,即
,即 ,
,
由
又

且
解得
17.(1)如图建立空间直角坐标系,设 ,且
,且
 由
由

∴

∴
∴SC与AD所成的角为
18.(1)最后甲获胜的概率为P1,乙获胜的概率为P2,则 ,∴甲、乙两队各自获胜的概率分
,∴甲、乙两队各自获胜的概率分
(2)乙队第五局必须获胜,前四局为独立重复实验,乙队3∶2获胜的概率为P3,则 ,∴乙队以3∶2获胜的概率为
,∴乙队以3∶2获胜的概率为
19.(1)联立两个方程,从中消去y得
∴
注意到a>b>c, a+b+c=0,∴a>0, c<0, ∴△>0, 故两条曲线必交于两个不同的交点A、B;
(2)设 的两个根为x1、x2,则AB在x轴上的射影的长
的两个根为x1、x2,则AB在x轴上的射影的长

由 ,由此可得
,由此可得
20.(1)设{an}的公差为d,则65=
∴
(2)设函数
故当x=e时 ,且当0<x<e时
,且当0<x<e时 ,当x>e时
,当x>e时 ,
,
∴函数 在区间(0,e)内单调递增,而在区间
在区间(0,e)内单调递增,而在区间 上单调递减,由
上单调递减,由 及函数
及函数 单调递增可知函数
单调递增可知函数 与f(x)有相同的单调性,即
与f(x)有相同的单调性,即 在区间(0,e)内单调递增,而在区间
在区间(0,e)内单调递增,而在区间 上单调递减,
上单调递减,
注意到 ,由2<e<3知数列{bn}的最大项是第2项,这一项是
,由2<e<3知数列{bn}的最大项是第2项,这一项是 ;
;
(3)在数列{cn}不存在这样的项使得它们按原顺序成等比数列. 事实上由
∴
有 . 综合知即无法找到这样的一些连续的项使其成等比数列.
. 综合知即无法找到这样的一些连续的项使其成等比数列.
21.(1)若直线l与x轴不垂直,设其方程为 ,l与抛物线
,l与抛物线 的交点坐标分别为
的交点坐标分别为 、
、 ,由
,由 得
得 ,即
,即 ,
,
则
 又由
又由 得
得 .
.
则 即
即 ,则直线l的方程为
,则直线l的方程为 ,
,
则直线l过定点(2,0).
若直线l与x轴垂直,易得 l的方程为x=2,
l的方程为x=2,
则l也过定点(2,0). 综上,直线l恒过定点(2,0).
(2)由(1)得 ,可得
,可得 解得k的取值范围是
解得k的取值范围是
(3)假定 ,则有
,则有 ,如图,即
,如图,即
由(1)得 . 由定义得
. 由定义得 从而有
从而有

 均代入(*)得
均代入(*)得
 ,即
,即 这与
这与 相矛盾.
相矛盾.
经检验,当 轴时,
轴时, . 故
. 故
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com