
2006年河南省示范性普通高中毕业班教学质量调研考试
理科数学
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
第I卷(选择题 共60分)
[参考公式]
如果事件A、B互斥,那么 球的表面积公式


如果事件A、B相互独立,那么 其中R表示球的半径

如果事件A在一次试验中发生的概率是 球的体积公式
P,那么n次独立重复试验中恰好发生k 
次的概率 其中R表示球的半径
其中R表示球的半径
一、选择题:
(1)若集合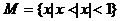 ,
,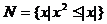 ,则
,则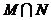 =
=
A. 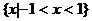 B.
B.
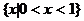
C. 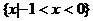 D.
D.
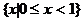
(2)已知等差数列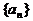 ,公差为
,公差为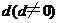 ,且
,且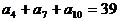 ,若
,若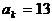 ,则k=
,则k=
A. 6 B.
(3)当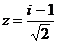 时,
时,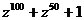 的值等于
的值等于
A. 1 B. -1 C. i D. -i
(4)设a≠0为常数,已知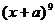 和
和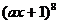 这两个展开式中
这两个展开式中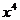 的系数相等,则a的值为
的系数相等,则a的值为
A. 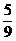 B.
B.
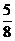 C.
C.
 D.
D.
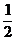
(5)曲线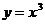 在点P处的切线斜率为k,当k=3时的P点坐标为
在点P处的切线斜率为k,当k=3时的P点坐标为
A. (-2,-8) B. (-1,-1),(1,1)
C. (2,8) D.
(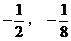 )
)
(6)函数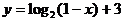 的反函数的解析式为
的反函数的解析式为
A. 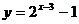 B.
B.
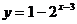
C. 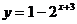 D.
D.
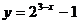
(7)为了得到函数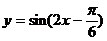 的图象,可以将函数
的图象,可以将函数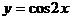 的图象
的图象
A. 向右平移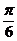 个单位长度 B.
向右平移
个单位长度 B.
向右平移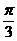 个单位长度
个单位长度
C. 向左平移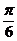 个单位长度 D.
向左平移
个单位长度 D.
向左平移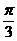 个单位长度
个单位长度
(8)函数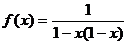 的最大值是
的最大值是
A. 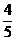 B.
B.
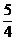 C.
C.
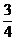 D.
D.
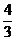
(9)在正方体ABCD―A1B1C1D1中,O为AC与BD的交点,则C1O与A1D所成的角为
A. 60° B.
90° C.
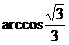 D.
D.
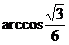
(10)设椭圆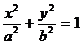 、双曲线
、双曲线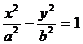 、抛物线
、抛物线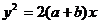 (其中
(其中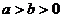 )的离心率分别为
)的离心率分别为 ,则下列结论正确的是
,则下列结论正确的是
① ②
②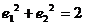
③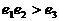 ④
④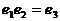 ⑤
⑤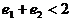
A. ①②⑤ B. ①② C. ②④ D. ③⑤
(11)点O是△ABC所在平面内一点,满足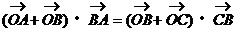 =
=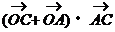 ,则点O是△ABC的
,则点O是△ABC的
A. 内心 B. 外心 C. 重心 D. 垂心
(12)函数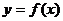 的图象关于直线
的图象关于直线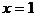 对称,则导函数
对称,则导函数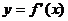 的图象
的图象
A. 关于直线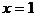 对称 B.
关于直线
对称 B.
关于直线 对称
对称
C. 关于点(1,0)对称 D. 关于点(-1,0)对称
第II卷(非选择题 共90分)
(13)若一个正方体的顶点都在同一球面上,则球与该正方体的体积之比为________。
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在题中横线上。
(14)已知x,y满足约束条件 ,则
,则 的最小值是________。
的最小值是________。
(15)已知点 ,其中n为正整数。设Sn表示△ABC外接圆的面积,则
,其中n为正整数。设Sn表示△ABC外接圆的面积,则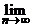
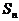 =___________。
=___________。
(16)对某种产品的6件不同正品和4件不同次品,一一进行测试,到区分出所有次品为止。若所有次品恰好在第五次测试被全部发现,则这样的测试方法有________种。(以数字作答)
(17)(本小题满分12分)
三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
已知函数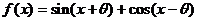 的定义域为R。
的定义域为R。
(I)当 时,求
时,求 的单调增区间;
的单调增区间;
(II)当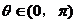 ,且
,且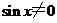 ,当
,当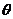 为何值时,
为何值时, 为偶函数。
为偶函数。
(18)(本小题满分12分)
一种电路控制器在出厂时每四件一等品装成一箱,工人在装箱时不小心把两件二等品和两件一等品装入了一箱,为了找出该箱中的二等品,我们对该箱中的产品逐一取出进行测试。
(I)求前两次取出的都是二等品的概率;
(II)用随机变量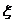 表示第二个二等品被取出时共取出的件数,求
表示第二个二等品被取出时共取出的件数,求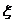 的分布列及数学期望。
的分布列及数学期望。
(19)(本小题满分12分)
如图,在直三柱锥ABC―A1B1C1中,∠ACB=90°,BC=CC1=a,AC=2a。
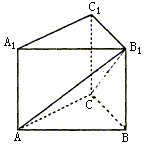
(I)求证:AB1⊥BC1;
(II)求二面角B―AB1―C的正切值;
(III)求点A1到平面AB1C的距离。
(20)(本小题满分12分)
设函数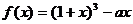 ,其中
,其中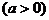 。
。
(I)求a的范围,使 在
在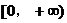 上是增函数;
上是增函数;
(II)函数 在
在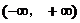 上能否是增函数?为什么?
上能否是增函数?为什么?
(21)(本小题满分14分)
已知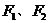 、D三点不在同一直线上,且
、D三点不在同一直线上,且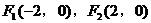 ,
,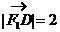 ,
,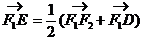 。
。
(I)求点E轨迹方程;
(II)过F1作直线以F1、F2为焦点的椭圆C于P、Q两点,线段PQ的中点到y轴的距离为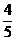 ,且直线PQ与点E的轨迹相切,求该椭圆的方程;
,且直线PQ与点E的轨迹相切,求该椭圆的方程;
(III)若该圆C的一个顶点T(0,-2),试问能否找到一条斜率为k(k≠0)的直线l,使l与椭圆C交于不同的两点M,N满足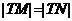 。
。
(22)(本小题满分12分)
四棱锥S-ABCD的所有棱长均为1米,一只小虫从S点出发沿四棱锥爬行,若在每一顶点处选择不同的棱都是等可能的。设小虫爬行n米后恰回到S点的概率为Pn。
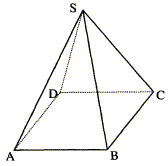
(I)求P2、P3的值;
(II)求证: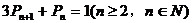 ;
;
(III)求证: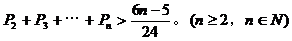
【试题答案】
2006年河南省示范性普通高中毕业班教学质量调研考试
一、选择题
(1)C (2)B (3)D (4)A (5)B
(6)B (7)B (8)D (9)D (10)A
(11)B (12)C
二、填空题
(13) (14)-6 (15)
(14)-6 (15) (16)576
(16)576
三、解答题
(17)(本小题满分12分)
解:(I)当 时,
时, 。
。
依条件有:
∴
∴ 的单调增区间为
的单调增区间为 6分
6分
(II)设
∴

∴
∴
依条件令 ,即
,即 时,
时, 为偶函数。 12分
为偶函数。 12分
(18)(本小题满分12分)
解:(I)四件产品逐一取出排成一列共有 种方法,前两次取出的产品都是二等品的共有
种方法,前两次取出的产品都是二等品的共有 种方法,∴前两次取出的产品都是二等品的概率为
种方法,∴前两次取出的产品都是二等品的概率为 ; 6分
; 6分
(II) 的所有可能取值为2,3,4,∴
的所有可能取值为2,3,4,∴ 的概率分布为
的概率分布为

2
3
4
P



∴ 12分
12分
(19)(本小题满分12分)
(I)证明:∵ABC-A1B1C1是直三棱柱,

∴CC1⊥平面ABC,∴AC⊥CC1。
∵AC⊥BC,∴AC⊥平面B1BCC1。
∴B1C是AB1在平面B1BCC1上的射影。
∵BC=CC1,∴四边形B1BCC1是正方形。
∴BC1⊥B1C。根据三垂线定理得
AB1⊥BC1 4分
(II)解:设 ,作OP⊥AB1于点P
,作OP⊥AB1于点P
连结BP,∵BO⊥AC,且BO⊥B1C,
∴BO⊥平面AB1C
∴OP是BP在平面AB1C上的射影。
根据三垂线定理得AB1⊥BP。
∴∠OPB是二面角B-AB1-C的平面角
∵
在Rt△POB中,
∴二面角B-AB1-C的正切值为 8分
8分
(III)解:解法1:∵A1C1∥AC,AC 平面AB1C,
平面AB1C,
∴A1C1∥平面AB1C。
∴点A1到平面AB1C的距离与点C1到平面AB1C的距离相等。
∵BC1⊥平面AB1C,
∴线段C1O的长度为点A1到平面AB1C的距离
∴点A1到平面AB1C的距离为 a 12分
a 12分
解法2:连结A1C,有 设点A1到平面AB1C的距离为h。
设点A1到平面AB1C的距离为h。
∵B1C1⊥平面ACC1A1,∴ ?h=
?h= ,
,
又
∴ ,
,
∴点A1到平面AB1C的距离为 12分
12分
(20)(本小题满分12分)
解:(I)若 在[0,
在[0, )上是增函数,则
)上是增函数,则 时
时
 恒成立
恒成立
即 恒成立
恒成立
∴
故a的取值范围是 6分
6分
(II)若 上是增函数
上是增函数
则 恒成立
恒成立
即 对所有的
对所有的 均成立
均成立
得 ,与题设
,与题设 矛盾。
矛盾。
∴ 上不是增函数 12分
上不是增函数 12分
(21)(本小题满分14分)
解:(I)设E(x,y),则
由已知得
∴
即为点E的轨迹方程。 4分
(II)设椭圆C的方程为 ,过F1的直线为
,过F1的直线为
 ,P、Q在椭圆C上,
,P、Q在椭圆C上,
∴
两式相减,得 ①
①
而 ,
,
代入①得 ②
②
由 与圆
与圆 相切,得
相切,得 代入②得
代入②得 ,
,
而 椭圆C的方程为
椭圆C的方程为 9分
9分
(III)假设存在直线 ,设MN的中点为
,设MN的中点为
由|TM|=|TN|,∴TP为线段MN的中垂线,其方程为
又设

相减并由
整理得:
又点P(-4k,2)在椭圆 的内部
的内部
∴ ,解之得
,解之得 ,即k不存在
,即k不存在
∴不存在直线l满足题设条件。 14分
(22)(本小题满分12分)
解:(I)P2表示从S点到A(或B、C、D),然后再回到S点的概率
所以 ;
;
因为从S点沿SA棱经过B或D,然后再回到S点的概率为 ,
,
所以 4分
4分
(II)设小虫爬行n米后恰回到S点的概率为Pn,那么 表示爬行n米后恰好没回到S点的概率,则此时小虫必在A(或B、C、D)点
表示爬行n米后恰好没回到S点的概率,则此时小虫必在A(或B、C、D)点
所以 8分
8分
(III)由
从而
所以

 12分
12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com