
2009届高考数学第三轮复习精编模拟三
参考公式:
如果事件 互斥,那么
球的表面积公式
互斥,那么
球的表面积公式


如果事件 相互独立,那么
其中
相互独立,那么
其中 表示球的半径
表示球的半径
 球的体积公式
球的体积公式
如果事件 在一次试验中发生的概率是
在一次试验中发生的概率是 ,那么
,那么

 次独立重复试验中事件
次独立重复试验中事件 恰好发生
恰好发生 次的概率
其中
次的概率
其中 表示球的半径
表示球的半径

第一部分 选择题(共50分)
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的
1、设集合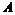 和
和 都是自然数集合
都是自然数集合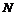 ,映射
,映射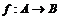 把集合
把集合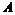 中的元素
中的元素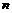 映射到集合
映射到集合 中的元素
中的元素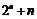 ,则在映射
,则在映射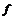 下,象20的原象是 ( )w.w.w.k.s.5.u.c.o.m
下,象20的原象是 ( )w.w.w.k.s.5.u.c.o.m
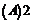
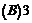
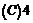
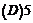
2、已知 、
、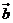 均为单位向量,它们的夹角为60°,那么|
均为单位向量,它们的夹角为60°,那么| +3
+3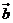 |= ( )
|= ( )
 A.
A.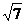 B
B
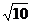 C.
C.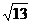 D.4
D.4
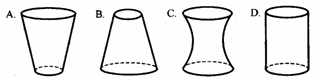
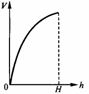 3、向高为
3、向高为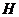 的水瓶中注水,注满为止,如果注水量
的水瓶中注水,注满为止,如果注水量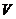 与水深
与水深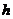 的函数关系的图象如右图所示,那么水瓶的形状是 ( )
的函数关系的图象如右图所示,那么水瓶的形状是 ( )
4、若x为三角形中的最小内角,则函数y=sinx+cosx的值域是( )
A.(1,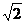
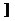 B.(0,
B.(0,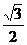
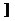 C.[
C.[ ,
,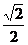 ] D.(
] D.( ,
,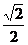
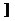
5、原市话资费为每3分钟0.18元,现调整为前3分钟资费为0.22元,超过3分钟的,每分钟按0.11元计算,与调整前相比,一次通话提价的百分率( )
A.不会提高70% B.会高于70%,但不会高于90%
C.不会低于10% D.高于30%,但低于100%
6、已知{an}是等差数列,a1=-9,S3=S7,那么使其前n项和Sn最小的n是( )
A.4 B.
7、设a,b是满足ab<0的实数,那么 ( )
A.|a+b|>|a-b| B.|a+b|<|a-b|
C.|a-b|<|a|-|b| D.|a-b|<|a|+|b|
8、棱长都为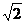 的四面体的四个顶点在同一球面上,则此球的表面积为( )
的四面体的四个顶点在同一球面上,则此球的表面积为( )
A、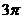 B、
B、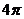 C、
C、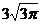 D、
D、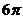
9、给定四条曲线:①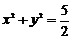 ,②
,②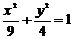 ,③
,③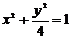 ,④
,④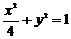 ,其中与直线
,其中与直线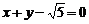 仅有一个交点的曲线是( )
仅有一个交点的曲线是( )
A. ①②③ B. ②③④ C. ①②④ D. ①③④
10、定义函数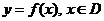 ,若存在常数C,对任意的
,若存在常数C,对任意的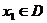 ,存在唯一的
,存在唯一的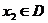 ,使得
,使得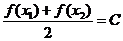 ,则称函数
,则称函数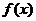 在D上的均值为C。已知
在D上的均值为C。已知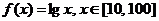 ,则函数
,则函数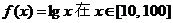 上的均值为( )
上的均值为( )
A、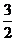 B、
B、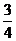 C、
C、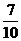 D、10
D、10
第二部分 非选择题(共100分)
二、填空题:本大题共5小题,其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.每小题5分,满分20分.
11、不等式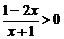 的解集是______。
的解集是______。
12、已知0<t<1,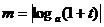 、
、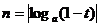 ,则
,则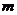 与
与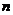 的大小关系为______.
的大小关系为______.
13、不论k为何实数,直线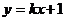 与曲线
与曲线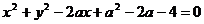 恒有交点,则实数a的取值范围是 。
恒有交点,则实数a的取值范围是 。
14、(坐标系与参数方程选做题) 在极坐标系中,已知直线过点(1,0),且其向上的方向与极轴的正方向所成的最小正角为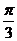 ,则直线的极坐标方程为______________.
,则直线的极坐标方程为______________.
15.(几何证明选讲选做题) 已知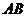 是半圆
是半圆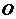 的直径,点
的直径,点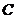 在半圆上,
在半圆上,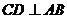 于点
于点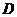 ,且
,且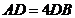 ,设
,设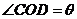 ,则
,则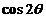 =
.
=
.
三.解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)
设全集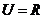 ,函数
,函数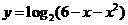 的定义域为A,函数
的定义域为A,函数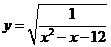 的定义域为B
的定义域为B
(Ⅰ)求集合 与
与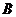 ;
;
(Ⅱ)求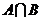 、
、
17.(本小题满分12分)
已知数列{an}、{bn}满足:a1=1,a2=a(a为实数),且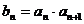 ,其中n=1,2,3,…
,其中n=1,2,3,…
(Ⅰ)求证:“若数列{an}是等比数列,则数列{bn}也是等比数列”是真命题;
(Ⅱ)写出(Ⅰ)中命题的逆命题;判断它是真命题还是假命题,并说明理由.
18.(本小题满分14分)
在一次考试中共有8道选择题,每道选择题都有4个选项,其中有且只有一个选项是正确的.评分标准规定:“每题只选一个选项,选对得5分,不选或选错得0分”.某考生已确定有4道题答案是正确的,其余题中:有两道只能分别判断2个选项是错误的,有一道仅能判断1个选项是错误的,还有一道因不理解题意只好乱猜,求:
(1)该考生得40分的概率;
(2)该考生得多少分的可能性最大?
(3)该考生所得分数的数学期望.
19. (本小题满分14分)
已知圆C: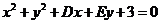 ,圆C关于直线
,圆C关于直线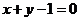 对称,圆心在第二象限,半径为
对称,圆心在第二象限,半径为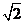
(Ⅰ)求圆C的方程;
(Ⅱ)已知不过原点的直线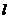 与圆C相切,且在x轴、y轴上的截距相等,求直线
与圆C相切,且在x轴、y轴上的截距相等,求直线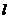 的方程。
的方程。
20. (本小题满分14分)
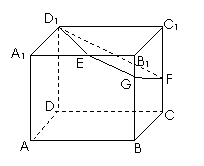 如图,已知正方体
如图,已知正方体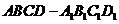 的棱长为2,E、F分别是
的棱长为2,E、F分别是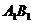 、
、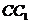 的中点,过
的中点,过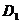 、E、F作平面
、E、F作平面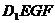 交
交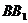 于G..
于G..
(Ⅰ)求证: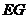 ∥
∥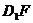 ;
;
(Ⅱ)求二面角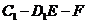 的余弦值;
的余弦值;
(Ⅲ)求正方体被平面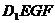 所截得的几何体
所截得的几何体
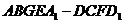 的体积.
的体积.
21.(本小题满分14分)
对于定义域为D的函数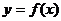 ,若同时满足下列条件:
,若同时满足下列条件:
①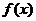 在D内单调递增或单调递减;
在D内单调递增或单调递减;
②存在区间[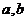 ]
]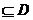 ,使
,使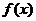 在[
在[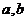 ]上的值域为[
]上的值域为[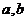 ];那么把
];那么把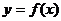 (
(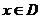 )叫闭函数。
)叫闭函数。
(Ⅰ)求闭函数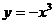 符合条件②的区间[
符合条件②的区间[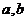 ];
];
(Ⅱ)判断函数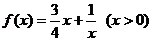 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(Ⅲ)若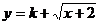 是闭函数,求实数
是闭函数,求实数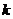 的取值范围。
的取值范围。
一.选择题:CCBAB BBADA
解析:1:由映射概念可知 可得
可得 .故选
.故选 .
.
2:如图, +3
+3 =
= ,在
,在 中,
中, 由余弦定理得|
由余弦定理得| +3
+3 |=|
|=| |=
|= ,故选C。
,故选C。
3:取 ,由图象可知,此时注水量
,由图象可知,此时注水量 大于容器容积的
大于容器容积的 ,故选B。
,故选B。
4:因 为三角形中的最小内角,故
为三角形中的最小内角,故 ,由此可得y=sinx+cosx>1,排除B,C,D,故应选A。
,由此可得y=sinx+cosx>1,排除B,C,D,故应选A。
5:取x=4,y=?100%≈-8.3%,排除C、D;取x=30,y = ?100%≈77.2%,排除A,故选B。
 6:等差数列的前n项和Sn=
6:等差数列的前n项和Sn= n2+(a1-
n2+(a1- )n可表示为过原点的抛物线,又本题中a1=-9<0,
S3=S7,可表示如图,由图可知,n=
)n可表示为过原点的抛物线,又本题中a1=-9<0,
S3=S7,可表示如图,由图可知,n= ,是抛物线的对称轴,所以n=5是抛物线的对称轴,所以n=5时Sn最小,故选B。
,是抛物线的对称轴,所以n=5是抛物线的对称轴,所以n=5时Sn最小,故选B。
7:∵A,B是一对矛盾命题,故必有一真,从而排除错误支C,D。又由ab<0,可令a=1,b= -1,代入知B为真,故选B。
8:借助立体几何的两个熟知的结论:(1)一个正方体可以内接一个正四面体;(2)若正方体的顶点都在一个球面上,则正方体的对角线就是球的直径。可以快速算出球的半径 ,从而求出球的表面积为
,从而求出球的表面积为 ,故选A。
,故选A。
9:分析选择支可知,四条曲线中有且只有一条曲线不符合要求,故可考虑找不符合条件的曲线从而筛选,而在四条曲线中②是一个面积最大的椭圆,故可先看②,显然直线和曲线 是相交的,因为直线上的点
是相交的,因为直线上的点 在椭圆内,对照选项故选D。
在椭圆内,对照选项故选D。
10: ,从而对任意的
,从而对任意的 ,存在唯一的
,存在唯一的 ,使得
,使得 为常数。充分利用题中给出的常数10,100。令
为常数。充分利用题中给出的常数10,100。令 ,当
,当 时,
时, ,由此得
,由此得 故选A。
故选A。
二.填空题:11、 ; 12、
; 12、 ; 13、
; 13、 ;
;
14、 ; 15、
; 15、 ;
;
解析:11:不等式 等价于
等价于 ,也就是
,也就是 ,所以
,所以 ,从而应填
,从而应填 .
.
12:  ,不论
,不论 的值如何,
的值如何, 与
与 同号,所以
同号,所以
13:题设条件等价于点(0,1)在圆内或圆上,或等价于点(0,1)到圆 的圆心的距离不超过半径,∴
的圆心的距离不超过半径,∴ 。
。
14.解:由正弦定理得 即
即 ,∴所求直线的极坐标方程为
,∴所求直线的极坐标方程为 .
.
15.解: 即
即 ,
,

三.解答题:
16.解:(Ⅰ)函数  要有意义需满足:
要有意义需满足: 即
即 ,解得
,解得 ,
, …………………………………3分
…………………………………3分
函数 要有意义需满足
要有意义需满足 ,即
,即 ,
,
解得 或
或
 …………………………………6分
…………………………………6分
(Ⅱ)由(Ⅰ)可知 ,
, ,
,
 ,
, ………………………12分
………………………12分
17.解:(I)因为 是等比数列,
是等比数列,
又 …………………………………………2分
…………………………………………2分

∴ 是以a为首项,
是以a为首项, 为公比的等比数列.………………………………6分
为公比的等比数列.………………………………6分
(II)(I)中命题的逆命题是:若 是等比数列,则
是等比数列,则 也是等比数列,是假命题.
也是等比数列,是假命题.
……………………………………………………………8分
设 的公比为
的公比为 则
则
又
 是以1为首项,q为公比的等比数列,
是以1为首项,q为公比的等比数列,
 是以
是以 为首项,q为公比的等比数列.……………………10分
为首项,q为公比的等比数列.……………………10分
即 为1,a,q,aq,q2,aq2,…
为1,a,q,aq,q2,aq2,…
但当q≠a2时, 不是等比数列
不是等比数列
故逆命题是假命题.……………………………………………………………………12分
另解:取a=2,q=1时,

因此 是等比数列,而
是等比数列,而 不是等比数列.
不是等比数列.
故逆命题是假命题.……………………………………………………………………12分
18.解:(1)设选对一道“可判断2个选项是错误的”题目为事件A,“可判断1个选项是错误的”该题选对为事件B,“不能理解题意的”该题选对为事件C.则 ---
---
所以得40分的概率 ………………………………4分
………………………………4分
(2) 该考生得20分的概率 =
= ……………………5分
……………………5分
该考生得25分的概率:

= ……………………6分
……………………6分
该考生得30分的概率: =
= =
=  --------------7分
--------------7分
该考生得35分的概率:

= ……………………9分
……………………9分
∵ ∴该考生得25分或30分的可能性最大………………………………11分
∴该考生得25分或30分的可能性最大………………………………11分
(3)该考生所得分数的数学期望 =
=
………………………………14分
19.解:(Ⅰ)由 知圆心C的坐标为
知圆心C的坐标为 --------------(1分)
--------------(1分)
∵圆C关于直线 对称
对称
∴点 在直线
在直线 上 -----------------(2分)
上 -----------------(2分)
即D+E=-2,------------①且 -----------------②-----------------(3分)
-----------------②-----------------(3分)
又∵圆心C在第二象限 ∴ -----------------(4分)
-----------------(4分)
由①②解得D=2,E=-4 -----------------(5分)
∴所求圆C的方程为: ------------------(6分)
------------------(6分)
(Ⅱ) 切线在两坐标轴上的截距相等且不为零,设
切线在两坐标轴上的截距相等且不为零,设 :
: -----------(7分)
-----------(7分)
 圆C:
圆C:
 圆心
圆心 到切线的距离等于半径
到切线的距离等于半径 ,
,
即
 。
------------------(12分)
。
------------------(12分)
所求切线方程 ------------------(14分)
------------------(14分)
20.(Ⅰ)证明:在正方体 中,∵平面
中,∵平面 ∥平面
∥平面
平面
 平面
平面
 ,平面
,平面
 平面
平面

 ∴
∴ ∥
∥ .-------------------------------------3分
.-------------------------------------3分
(Ⅱ)解:如图,以D为原点分别以DA、DC、DD1为
x、y、z轴,建立空间直角坐标系,则有
D1(0,0,2),E(2,1,2),F(0,2,1),
∴ ,
,
设平面 的法向量为
的法向量为 
则由 ,和
,和 ,得
,得 ,
,
取 ,得
,得 ,
, ,∴
,∴ ------------------------------6分
------------------------------6分
又平面 的法向量为
的法向量为 (0,0,2)
(0,0,2)
故 ;
;
∴截面 与底面
与底面 所成二面角的余弦值为
所成二面角的余弦值为 . ------------------9分
. ------------------9分
(Ⅲ)解:设所求几何体 的体积为V,
的体积为V,
∵ ~
~ ,
, ,
, ,
,
∴ ,
, ,
,
∴ ,
,
 --------------------------11分
--------------------------11分
故V棱台


∴V=V正方体-V棱台
 . ------------------14分
. ------------------14分
21.解:(Ⅰ)由题意, 在[
在[ ]上递减,则
]上递减,则 解得
解得
所以,所求的区间为[-1,1] ………………………4分
(Ⅱ)取 则
则 ,即
,即 不是
不是 上的减函数。
上的减函数。
取
 ,
,
即 不是
不是 上的增函数
上的增函数
所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。-------9分
(Ⅲ)若 是闭函数,则存在区间[
是闭函数,则存在区间[ ],在区间[
],在区间[ ]上,函数
]上,函数 的值域为[
的值域为[ ],即
],即 ,
, 为方程
为方程 的两个实数根,
的两个实数根,
即方程 有两个不等的实根。
有两个不等的实根。
当 时,有
时,有 ,解得
,解得 。
。
当 时,有
时,有 ,无解。
,无解。
综上所述, ---------------------------------------------14分
---------------------------------------------14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com