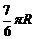|
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
22.(本小题满分14分) 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情

2009届师大附中、鹰潭一中高三联考 试题详情
一、选择题 1--5 DDCBA 6--10 ADBCA 11-12 AB 二、填空题 13. 14.12 15. 14.12 15. 16.AC 16.AC 三、解答题 17.解:(Ⅰ)  , ,  , ,
 . .
 , ,
 , ,  . .
(Ⅱ)由余弦定理 ,得 ,得  . .  , ,  . .
所以 的最小值为 的最小值为 ,当且仅当 ,当且仅当 时取等号. 时取等号. 18、(Ⅰ)解法一:依据题意,因为队伍从水路或陆路抵达灾区的概率相等,则将“队伍从水路或陆路抵达灾区”视为同一个事件. 记“队伍从水路或陆路抵达灾区”为事件C,且B、C相互独立,而且 .…………………………………… 2分 .…………………………………… 2分 在5月13日恰有1支队伍抵达灾区的概率是  . ……………… 5分 . ……………… 5分
解法二:在5月13日恰有1支队伍抵达灾区的概率是 
 .……………………………………………………………… 5分 .……………………………………………………………… 5分
(Ⅱ)依据题意,因为队伍从水路或陆路抵达灾区的概率相等,则将“队伍从水路或陆路抵达灾区”视为同一个事件. 记“队伍从水路或陆路抵达灾区”为事件C,且B、C相互独立,而且 . . 设5月13日抵达灾区的队伍数为 ,则 ,则 =0、1、2、3、4. ……………… 6分 =0、1、2、3、4. ……………… 6分 由已知有: ;………………………………… 7分 ;………………………………… 7分  ;………………………… 8分 ;………………………… 8分
 ;………………… 9分 ;………………… 9分
 ;……………………… 10分 ;……………………… 10分
 . ………………………………………………… 10分 . ………………………………………………… 10分
因此其概率分布为: 
0 1 2 3 4 P 




……………… 11分 所以在5月13日抵达灾区的队伍数 的数学期望为: 的数学期望为:  =0× =0× + 1× + 1× + 2× + 2× + 3× + 3× + 4× + 4× = = . .
答:在5月13日抵达灾区的队伍数 的数学期望 的数学期望 = = . ………………
12分 . ………………
12分 19.(I)由已知a2-a1=-2, a3-a2=-1, -1-(-2)=1 ∴an+1-an=(a2-a1)+(n-1)?1=n-3 n≥2时,an=( an-an-1)+(
an-1-an-2)+…+( a3-a2)+(
a2-a1)+ a1
=(n-4)+(n-5) +…+(-1)+(-2)+6 = n=1也合适. ∴an= (n∈N*) ……………………3分 (n∈N*) ……………………3分 又b1-2=4、b2-2=2 .而 ∴bn-2=(b1-2)?( ∴bn-2=(b1-2)?( )n-1即bn=2+8?( )n-1即bn=2+8?( )n )n ∴数列{an}、{bn}的通项公式为:an= ,bn=2+( ,bn=2+( )n-3…………… 6分 )n-3…………… 6分 (II)设 当k≥4时 为k的增函数,-8?( 为k的增函数,-8?( )k也为k的增函数,…………… 8分 )k也为k的增函数,…………… 8分  而f(4)= 而f(4)=  ∴当k≥4时ak-bk≥ ∴当k≥4时ak-bk≥ ………………10分 ………………10分
又f(1)=f(2)=f(3)=0 ∴不存在k, 使f(k)∈(0, )…………12分 )…………12分 20、证(Ⅰ)因为 侧面 侧面 ,故 ,故 在 中, 中, 由余弦定理有 由余弦定理有 
 故有 故有

而  且 且 平面 平面   ……………… 4分 ……………… 4分 (Ⅱ)由 从而 且 且 故 故 不妨设  ,则 ,则 ,则 ,则 又 则 则 在 中有 中有
 从而 从而 (舍去) (舍去) 故 为 为 的中点时, 的中点时, ……………… 8分 ……………… 8分 法二:以 为原点 为原点 为 为 轴,设 轴,设 ,则 ,则  由 由 得 得 
即  化简整理得   或 或  当 时 时 与 与 重合不满足题意 重合不满足题意 当 时 时 为 为 的中点 的中点 故 为 为 的中点使 的中点使 ……………… 8分 ……………… 8分 (Ⅲ)取 的中点 的中点 , , 的中点 的中点 , , 的中点 的中点 , , 的中点 的中点 连 则 则 ,连 ,连 则 则 ,连 ,连 则 则 连 则 则 ,且 ,且 为矩形, 为矩形, 又 故 故 为所求二面角的平面角……………… 10分 为所求二面角的平面角……………… 10分  在 在 中, 中,

 ……………… 12分 ……………… 12分
法二:由已知 ,
所以二面角 ,
所以二面角 的平面角 的平面角 的大小为向量 的大小为向量 与 与 的夹角……………… 10分 的夹角……………… 10分 因为  故  ……………… 12分 ……………… 12分 21.解:(I)由 , ,
 ∴直线l的斜率为 ∴直线l的斜率为 , , 故l的方程为 ,∴点A坐标为(1,0)……… 2分 ,∴点A坐标为(1,0)……… 2分 设 则 则 , , 由 得 得
 整理,得 ……………………4分 ……………………4分 ∴动点M的轨迹C为以原点为中心,焦点在x轴上,长轴长为 ,短轴长为2的椭圆 …… 5分 ,短轴长为2的椭圆 …… 5分 (II)如图,由题意知直线l的斜率存在且不为零,设l方程为y=k(x-2)(k≠0)①

 , ,
由△>0得0<k2< . ……………… 6分 . ……………… 6分 设E(x1,y1),F(x2,y2),则 ②……………………………7分 ②……………………………7分 令 , , 由此可得 ……………… 8分 ……………… 8分 由②知 
 . .
∴△OBE与△OBF面积之比的取值范围是(3-2 ,1).…………12分 ,1).…………12分 22解:(1)由题意知, 的定义域为 的定义域为 , ,  …… 2分 …… 2分
 当 当 时, 时,
 ,函数 ,函数 在定义域 在定义域 上单调递增.
… 3分 上单调递增.
… 3分
(2) ①由(Ⅰ)得,当 时, 时, ,函数 ,函数 无极值点.……………… 5分 无极值点.……………… 5分
②当 时, 时, 有两个不同解, 有两个不同解, 
 时, 时, , , , ,
此时  , , 随 随 在定义域上的变化情况如下表: 在定义域上的变化情况如下表: 








减 极小值 增 由此表可知: 时, 时, 有惟一极小值点 有惟一极小值点 , …… 7分 , …… 7分 ii) 当 时,0< 时,0< <1 此时, <1 此时, , , 随 随 的变化情况如下表: 的变化情况如下表: 












增 极大值 减 极小值 增 由此表可知: 时, 时, 有一个极大值 有一个极大值 和一个极小值点 和一个极小值点 ;…9分 ;…9分 综上所述:当 时, 时, 有惟一最小值点 有惟一最小值点 ; ; 当 时, 时, 有一个极大值点 有一个极大值点 和一个极小值点 和一个极小值点  …….10分 …….10分
(3)由(2)可知当 时,函数 时,函数 ,此时 ,此时 有惟一极小值点 有惟一极小值点 且 …… 9分
…… 9分  …… 11分
…… 11分
令函数  …… 12分
…… 12分  …14分 …14分
| | | 



 ( )
( )
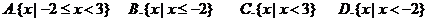

 对应的点位于( )
对应的点位于( )

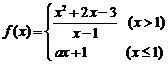 在点
在点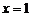 处连续,则
处连续,则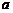 的值是 ( )
的值是 ( )
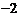 C.3 D.
C.3 D.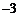

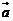 与
与 的夹角为
的夹角为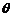 ,定义
,定义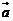 与
与 的“向量积”:
的“向量积”: 是一个向量,它的模
是一个向量,它的模 ,若
,若 ,则
,则 ( )
( )
 B.2 C.
B.2 C.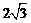 D.4
D.4
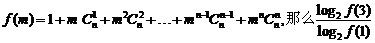 等于( )
等于( )
 C.1 D.3
C.1 D.3
 6.将1、2、3、…、9这九个数字填在图中的9个空格中,要求每一
行从左到右依次增大,每一列从上到下依次增大,当3、4固定在图中的位置 时,填写空格的办法有( )
6.将1、2、3、…、9这九个数字填在图中的9个空格中,要求每一
行从左到右依次增大,每一列从上到下依次增大,当3、4固定在图中的位置 时,填写空格的办法有( )


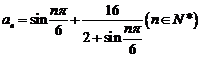 ,则数列
,则数列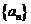 的最小值为( )
的最小值为( )
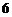 B.
B.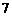 C.
C. D.
D.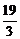

 的球内有一内接正三棱锥,它的底面三个顶点恰好都在同一个大圆上,一个动点从三棱锥的一个顶点出发沿球面运动,经过其余三点后返回,则经过的最短路程是( )
的球内有一内接正三棱锥,它的底面三个顶点恰好都在同一个大圆上,一个动点从三棱锥的一个顶点出发沿球面运动,经过其余三点后返回,则经过的最短路程是( )
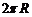 B.
B.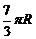 C.
C.
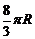 D.
D.