
2009年广东省古镇高三第二次质量检查
数学(文科)试卷
本试卷分第I卷(选择题)和第II卷(非选择题)两部分.共150分,考试时间120分钟.
第I卷(选择题,共60分)
一、选择题:(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。)
1、一组数据中的每一个数据都减去80,得到新数据,若求得新数据和平均数是1.2,则原来数据的平均数是
A. B.
B. C.
C.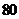 D.不能确定
D.不能确定
2、已知点 与点
与点 关于直线
关于直线 对称,则直线
对称,则直线 的方程为
的方程为
A. B.
B. C.
C. D.
D.
3、设 、
、 是两个集合,定义
是两个集合,定义 ,若
,若 ,
,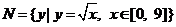 则
则
A. B.
B. C.
C. D.
D.
 4、已知函数
4、已知函数 ,不等式
,不等式 的解集为
的解集为 ,则函数
,则函数 的图象为
的图象为

5、已知分段函数 ,求函数的函数值的程框图如图。
,求函数的函数值的程框图如图。
有两个判断框内要填写的内容分别是
A. B.
B. 
C. D.
D.
6、直线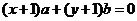 与圆
与圆 的位置关系是
的位置关系是
A.相交 B.相离 C.相切或相离 D.相切或相交
 7、如图,在正三角形
7、如图,在正三角形 中,
中, 、
、 、
、 分别是各边的中点,
分别是各边的中点,
 、
、 、
、 、
、 分别为
分别为 、
、 、
、 、
、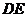 的中点,将
的中点,将
△ 沿折成
沿折成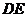 ,
, 、
、 三棱锥以后,
三棱锥以后, 与
与 所成角
所成角
的度数为( )
A. B.
B. C.
C. D.
D.
8、在△ 中,
中, ,
, ,
, ,则
,则 ( )
( )
A. 或
或 B.
B. C.
C. D.
D.
 9、如图,设
9、如图,设 是半径为
是半径为 的圆周上一个定点,在圆周上等可能地任取一点
的圆周上一个定点,在圆周上等可能地任取一点 ,连结
,连结 ,则弦
,则弦 的长超过
的长超过 的概率为( )
的概率为( )
A. B.
B. C.
C. D.
D.
10、在数列 中,
中, ,
, ,设
,设 为数列
为数列 的前
的前 项和,则
项和,则 ( ).
( ).
A. B.
B. C.
C.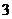 D.
D.
第II卷(非选择题 共100分)
二、填空题(本大题共4小题,每小题5分,共20分。把答案填在题中横线上)
 11.为了解初中生的身体素质,某地区随机抽取了
11.为了解初中生的身体素质,某地区随机抽取了
n名学生进行跳绳测试,根据所得数据画样本的频
率分布直方图所示,且从左到右第一小组的频
数是100,则 。
。
12、已知复数 与
与 均是纯虚数,则
均是纯虚数,则 。
。
13、在 △
△ 中,
中, ,
, ,则
,则 △
△ 的外接圆半径为
的外接圆半径为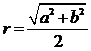 ,将此结论类比到空间,类似的结论
,将此结论类比到空间,类似的结论
。
▲  14.选做题:在下面两道小题中选做一题,两道小题都选的只计算第14小题的得分。
14.选做题:在下面两道小题中选做一题,两道小题都选的只计算第14小题的得分。
(1)如图,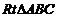 中,
中, ,
,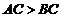 ,
, 于点
于点 ,若
,若 ,
,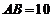 则
则 的值为
。
的值为
。
(2)已知抛物线 :
: ,(
,( 为参数)设
为参数)设 为坐标原点,点
为坐标原点,点 在
在 上运动,点
上运动,点 是线段
是线段 的中点,则点
的中点,则点 的轨迹方程为 。
的轨迹方程为 。
三、解答题:(共6小题)
15、(12分)已知 。
。
(1)若 ,求
,求 的值;
的值;
(2)求 的周期及递增区间。
的周期及递增区间。
 16、(14分)一个多面体的直观图、主视图、侧视图、俯视图如下所示,
16、(14分)一个多面体的直观图、主视图、侧视图、俯视图如下所示,
 、
、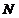 分别为
分别为 、
、 的中点。
的中点。
(1)求证: 平面
平面
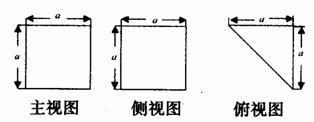 (2)求证:
(2)求证: 平面
平面
17、(12分)已知数列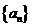 ,
, 前
前 项和为
项和为 ,对于任意的
,对于任意的 
 ,
, ,
, 、
、 总成等差数列。
总成等差数列。
(1)求 、
、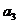 、
、 的值;(2)求通项
的值;(2)求通项 。
。
18、(14分)某工厂今年1月,2月,3月生产某产品分别为1万件, 万件,
万件,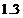 万件,为估计以后每月的产量,以这三个月的产量为依据,用一个函数模型替代该产品的月产量
万件,为估计以后每月的产量,以这三个月的产量为依据,用一个函数模型替代该产品的月产量 与月份
与月份 的关系,模型函数可选用二次函数或
的关系,模型函数可选用二次函数或 ,已知4月份该产品的产量为
,已知4月份该产品的产量为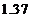 万件,请问:用以上哪个函数作模型较好?说明你的理由.
万件,请问:用以上哪个函数作模型较好?说明你的理由.
19、若函数 ,当
,当 时,函数
时,函数 有极值为
有极值为 ,
,
(1)求函数 的解析式;
的解析式;
(2)若 有3个解,求实数
有3个解,求实数 的取值范围。(14分)
的取值范围。(14分)
20、已知直线 过
过 与抛物线
与抛物线 交于
交于 、
、 两点,
两点, ,为坐标原点,且满足
,为坐标原点,且满足 ,
, 在
在 轴右侧。
轴右侧。
(1)求动点 的轨迹
的轨迹 的方程,
的方程,
(2)试曲线 的切线斜率为
的切线斜率为 ,满足
,满足 ,点
,点 到
到 轴的距离为
轴的距离为 ,求
,求 的取值范围。(14分)
的取值范围。(14分)
一、选择题:1、A2、A3、B4、B5、C6、D7、B8、D9、D10、A
二、填空题:11、1000
12、 13、三条侧棱
13、三条侧棱 、
、 、
、 两两互相垂直的三棱锥
两两互相垂直的三棱锥 中,
中, ,则此三棱锥的外接球半径为
,则此三棱锥的外接球半径为 14、(1)8 (2)
14、(1)8 (2)
三、解答题:
15、(1)∵ , ∴
, ∴ ,
………(2分)
,
………(2分)
∴ ,( 4分)
,( 4分) ,………(6分)
,………(6分)
∴ 或
或
所求解集为 ………(8分)
………(8分)
(2)∵
∴ ………(10分)
………(10分)
∴ ………(12分)
………(12分)

求 的周期为
的周期为 ,
,
递增区间
16、解:解析:由题意可知,这个几何体是直三棱柱,且 ,
, ,
,
(1)连结 ,
, 。
。
由直三棱柱的性质得 平面
平面 ,所以
,所以 ,则
,则
四边形 为矩形.
为矩形.
由矩形性质得, 过
过 的中点
的中点
在 中,由中位线性质,得
中,由中位线性质,得 ,
,
又 平面
平面 ,
, 平面
平面 ,
,
所以 平面
平面 。 (6分)
。 (6分)
(2)因为 平面
平面 ,
, 平面
平面 ,所以
,所以 ,
,
在正方形 :中,
:中, 。
。
又因为 ,所以
,所以 平面
平面 .
.
由 ,得
,得 平面
平面 . (14分)
. (14分)
17、解:(1)由题意知 ,
,
∴
由 ,可得
,可得

 (6分)
(6分)
(2)当 时,∵
时,∵
∴ ,两式相减得
,两式相减得
∴
 为常数,
为常数,
∴ ,
, ,
, ,…,
,…, 成等比数列。
成等比数列。
其中
 ,∴
,∴ ………(12分)
………(12分)
18、解:设二次函数 ,则
,则 ,解得
,解得
∴
将 代入上式:
代入上式:
而 对于,由已知,得:
对于,由已知,得: ,解得
,解得
∴
将 代入:
代入:
而4月份的实际产量为万件,相比之下,1.35比1.3更接近1.37.
∴选用函数作模型函数较好.
19、(1) ………(2分)
………(2分)
(1)由题意; ,解得
,解得 ,
,
∴所求的解析式为 ………(6分)
………(6分)
(2)由(1)可得
令 ,得
,得  或
或 , ………(8分)
, ………(8分)
∴当 时,
时,  ,当
,当 时,
时,  ,当
,当 时,
时, 
 因此,当
因此,当 时,
时,  有极大值
有极大值 ,………(8分)
,………(8分)
当 时,
时,  有极小值
有极小值 ,………(10分)
,………(10分)
∴函数 的图象大致如图。
的图象大致如图。
由图可知: 。………(14分)
。………(14分)
20、解:(1)直线 与
与 轴垂直时与抛物线交于一点,不满足题意.
轴垂直时与抛物线交于一点,不满足题意.
设直线 的方程为
的方程为 ,代入
,代入 得,
得,
 设
设 、
、 、
、
则 ,且
,且 ,即
,即 或
或 .
.
∴ ,
, 为
为 的中点.
的中点.
∴
∴ 由
由 或
或 得
得 或
或 .由
.由 在
在 轴右侧得.
轴右侧得. 
轨迹 的方程为
的方程为 .
.
(2)∵曲线 的方程为
的方程为 。
。
∴ ∴
∴  ,
,
 ,
, 且
且
∴ 又
又 ,
, ,
,
∴ ,
,
∴ ,∴
,∴
∴ 的取值范围为
的取值范围为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com