
2007年天津市十二区县重点学校高三毕业班联考(一)
数学试卷(文科)
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟。第Ⅰ卷1至2页,第Ⅱ卷3至8页。考试结束后,将II卷和答题卡一并交回。
祝各位考生考试顺利!
第I卷 (选择题,共50分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2.选出答案后,用铅笔把答题卡上对应的题目的答案标号涂黑,如需改动,用橡皮擦干净后,再填涂其它答案,不能答在试卷上.
参考公式:
如果事件A、B互斥,那么 球的体积公式


如果事件A、B相互独立,那么 其中R表示球的半径
 =
= 柱体(棱柱、圆柱)的体积公式
柱体(棱柱、圆柱)的体积公式
如果事件A在一次试验中发生的概率 V柱体=Sh
是P,那么n次独立重复试验中恰好发 其中S表示柱体的底面积,
生k次的概率 Pn(k)= Pk(1-P)n-k
h表示柱体的高。
Pk(1-P)n-k
h表示柱体的高。
一. 选择题(本题共10个小题,每小题5分,共50分。在每小题给出的四个选项中,有且只有一个是正确的)
1.设全集 ,集合
,集合 ,
, ,则
,则 等于( )
等于( )
A. B.
B. C.
C. D.
D.
2.不等式 的解集是
的解集是
A. B.
B. C.
C. D.
D.
3. 若抛物线 的焦点与双曲线
的焦点与双曲线 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )
A. B.
B. C.
C. D.
D.
4.设m,n是两条不同的直线,α、β是两个不同的平面,考查下列命题,其中正确的命题是( )
A.m⊥α,n β,m⊥n
β,m⊥n α⊥β
B.α∥β,m⊥α,n∥β
α⊥β
B.α∥β,m⊥α,n∥β m⊥n
m⊥n
C.α⊥β,m⊥α,n∥β m⊥n
D.α⊥β,α∩β=m,m⊥n
m⊥n
D.α⊥β,α∩β=m,m⊥n n⊥β
n⊥β
 5. 函数
5. 函数 的反函数的图象是
的反函数的图象是
A. B. C. D.
6. 在平面上有A、B、C三点,满足 ,
, ,则
,则
 的值为 A.4 B.
的值为 A.4 B. C.
C.  D.
D. 
7. 在1,2,3,4,5这五个数字组成的没有重复数字的三位数中,各位数字之和为偶数的共有
A.36个 B.24个 C.18个 D. 6个
8. 已知y = f (x)是偶函数,当x > 0时, ;若当
;若当 时,n≤f (x)≤m恒成立,则m ? n的最小值是
时,n≤f (x)≤m恒成立,则m ? n的最小值是
A. B.
B. C.1 D.
C.1 D.
9.对于平面上的点 有如下命题,
有如下命题, 和
和 ,则
,则 是
是 的
的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
10. 设函数 的定义域为
的定义域为 ,若存在与
,若存在与 无关的正常数
无关的正常数 使
使 对一切实数
对一切实数 均成立,则称
均成立,则称 为“有界泛函”.给出以下函数:①
为“有界泛函”.给出以下函数:① ②
② ③
③ ④
④
其中是“有界泛函”的个数为
A.0 B.
2006年天津市十二区县重点学校高三毕业班联考(一)
数学试卷(文科)
第Ⅱ卷 (非选择题,共100分)
注意事项:
1.第Ⅱ卷共6页,用蓝、黑色的钢笔或圆珠笔直接答在试卷中。
2.答卷前,请将密封线内的项目填写清楚。
题号
二
三
总分
17
18
19
20
21
22
分数
得分
评卷人
二.填空题:本大题共6小题,每小题4分,共24分.把答案填在答题卷中相应的横线上.
11.
设g(x)= 则g[g(
则g[g( )]=___________________.
)]=___________________.
12. 已知二项式 (
( 为常数)的展开式中的常数项为160,则
为常数)的展开式中的常数项为160,则 的值是________.
的值是________.
13.双曲线 上的点到左焦点的距离与到左准线的距离的比是3,则
上的点到左焦点的距离与到左准线的距离的比是3,则 等于 .
等于 .
14.在等比数列 中,
中, ,则
,则 的值等于______.
的值等于______.
15. 一个棱长为2的正八面体的六个顶点都在一个球面上,则球心到正八面体的一个侧面的距离等于_________________.
16.给出下列四个命题:①方程 可表示经过点
可表示经过点 的所有直线;②经过点
的所有直线;②经过点 且与直线
且与直线 垂直的直线方程一定能写成
垂直的直线方程一定能写成 的形式;③对任意实数
的形式;③对任意实数 ,直线
,直线 总与某一个定圆相切;④过定圆
总与某一个定圆相切;④过定圆 上的定点
上的定点 作圆的动弦
作圆的动弦 ,若
,若 ,则动点
,则动点 的轨迹为椭圆.其中所有真命题的序号为_______________.
的轨迹为椭圆.其中所有真命题的序号为_______________.
三.解答题:本大题6小题,共76分.解答应写出文字说明,证明过程或演算步骤.
得分
评卷人
17.(本小题满分12分)
设函数
(Ⅰ)若f(x)的最小正周期为 的值域
的值域
(Ⅱ)若函数f(x)的图象的一条对称轴方程为 的值
的值
得分
评卷人
18. (本小题满分12分)
已知函数 .
.
(Ⅰ)若x=3是 的极值点,求
的极值点,求 在
在 [1,a]上的最小值和最大值.
[1,a]上的最小值和最大值.
(Ⅱ)若 在
在 [1,+∞
[1,+∞ 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;
得分
评卷人
19. (本小题满分12分)
 已知多面体
已知多面体 中,
中, 平面
平面
 平面
平面
 为
为 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求异面直线 所成角余弦值;
所成角余弦值;
(Ⅲ)求面 和面
和面 所成二面角的大小.
所成二面角的大小.
得分
评卷人
 20. (本小题满分12分)
20. (本小题满分12分)
中央二台经济生活频道,主持人高博在主持“购物街”栏目中,其中有一个中奖游戏,该游戏规则是这样的:一个木质均匀的标有20等分数字格的转盘(如图),甲乙两名入选观众,每人都有两次转动转盘的机会,转盘停止时指针所指的两次数字之和为该人的得分,但超过100分按0分记,得分多者为优胜。每位入选者在转动一次后,认为分值理想时可以放弃第二次机会,游戏进行中,第一名选手甲通过一次转动后,指针所指的数字是85.
(Ⅰ)如果甲选择第二次转动,求甲得0分的概率.
(Ⅱ)如果甲放弃了第二次机会,求乙选手获胜的概率;
得分
评卷人
21. (本小题共14分)
已知点列 在直线
在直线 上,P1为直线
上,P1为直线 轴的交点,等差数列
轴的交点,等差数列 的公差为1
的公差为1  .
.
(Ⅰ)求 、
、 的通项公式;
的通项公式;
(Ⅱ) ;
;
(Ⅲ)若 ,
,
试证数列 为等比数列;并求
为等比数列;并求 的通项公式.
的通项公式.
得分
评卷人
22.(本小题满分14分)
 如图,已知椭圆C:
如图,已知椭圆C: ,经过椭圆C的右焦点F且斜率为k(k≠0)的直线
,经过椭圆C的右焦点F且斜率为k(k≠0)的直线 交椭圆G于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.
交椭圆G于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.
(Ⅰ)是否存在k,使对任意 >0,总有
>0,总有 成立?若存在,求出所有k的值;
成立?若存在,求出所有k的值;
(Ⅱ)若 ,求实数k的取值范围.
,求实数k的取值范围.
2007年天津市十二区县重点学校高三毕业班联考
数学答案(文科)
一.选择题:(本题共10个小题,每小题5分,共50分。)BADB DCAC BC
二.填空题:本大题共6小题,每小题4分,共24分.
11:1 12:-2
13:
14:9
15: 16:②③
16:②③
三.解答题:本大题共6小题,共74分.
17. (本小题满分12分)
解:解:
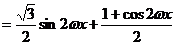 (2分)
(2分)
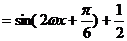 (4分)
(4分)
(Ⅰ) (6分)
(6分)
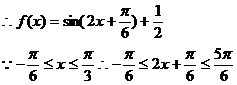
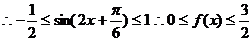 (8分)
(8分)
(Ⅱ)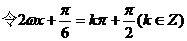 (10分)
(10分)
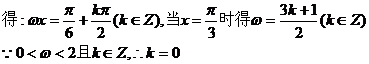
 (12分)
(12分)
18.(本小题满分12分)
解:(Ⅰ)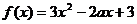 --------1分
--------1分
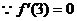 ,即27
,即27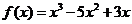 .---------2分
.---------2分
令 得
得 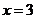 ,或
,或 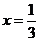 (舍去) ------------------3分
(舍去) ------------------3分
当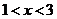 时,
时,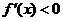 ; 当
; 当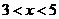 时,
时,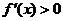 -----------------5分
-----------------5分
即当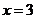 时,
时,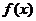 有极小值
有极小值 .又
.又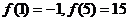
∴ f(x)在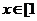 ,
,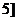 上的最小值是
上的最小值是 ,最大值是
,最大值是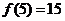 . ----------7分
. ----------7分
(Ⅱ)令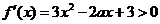 .
.
∵ x≥1. ∴ 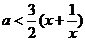 ,------------------------------------------------------9分
,------------------------------------------------------9分
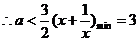 (当x=1时,取最小值).
(当x=1时,取最小值).
∴ a<3(a=3时也符合题意). ∴ a≤3.------------------------------------12分.
19.(本小题满分12分)
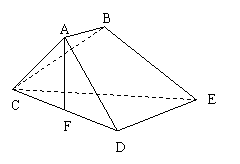
解:(Ⅰ)∵DE⊥平面ACD,AF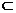 平面ACD ∴DE⊥AF
(2分)
平面ACD ∴DE⊥AF
(2分)
又∵AC=AD=CD,F为CD中点
 ∴AF⊥CD,又∵CD∩D∴AF⊥平面CDE
(4分)
∴AF⊥CD,又∵CD∩D∴AF⊥平面CDE
(4分)
(Ⅱ)∵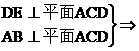 DE∥AB
DE∥AB
取DE中点M,连结AM、CM,
则四边形AMEB为平行四边形
AM∥BE,则∠CAM为AC与BE所成的角 (6分)
在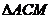 中,AC=
中,AC=
AM=
CM=
由余弦定理得,,
∴异面直线AC、BE所成的角的余弦值为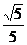 (8分)
(8分)
(Ⅲ)延长DA,EB交于点G,连结CG
因为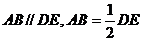 ,所以A为GD中点
(9分)
,所以A为GD中点
(9分)
又因为F为CD中点,所以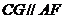 (10分)
(10分)
因为AF⊥平面CDE,所以CG⊥平面CDE
故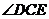 为面
为面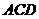 和面
和面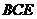 所成二面角的平面角
(11分)
所成二面角的平面角
(11分)
易求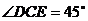 (12分)
(12分)
20. (本小题满分12分)
解:(Ⅰ) 甲得0分的概率为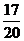 -----------------4分
-----------------4分
(Ⅱ)当乙1次赢取甲的概率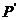 =
=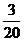 (
(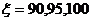 )-------------------6分
)-------------------6分
当乙2次赢取甲的概率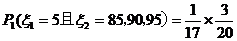 ----------8分
----------8分
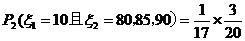 -
-
……………
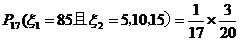 --------10分
--------10分
(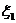 、
、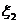 分别表示第一次、第二次转动时指针所指分数)
分别表示第一次、第二次转动时指针所指分数)
P=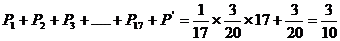 -------------------12分
-------------------12分
21. (本小题满分14分)
解:(Ⅰ) 在直线
在直线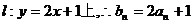 ------1分
------1分
∵P1为直线l与y轴的交点,∴P1(0,1) 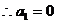 , ------2分
, ------2分
又数列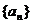 的公差为1
的公差为1 
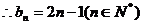 ------4分
------4分
(Ⅱ)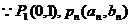
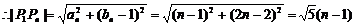 ------5分
------5分
 -----7分
-----7分
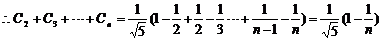 ----------8分
----------8分
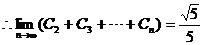 -
----------9分
-
----------9分
(Ⅲ)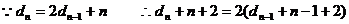 ---------12分
---------12分
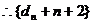 是以2为公比,4为首项的等比数列,
是以2为公比,4为首项的等比数列,
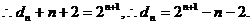 ----------------14分
----------------14分
22.(本小题满分14分)
(Ⅰ)椭圆C: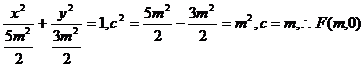 2分
2分
直线AB:y=k(x-m), 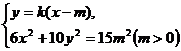 ,(10k2+6)x2-20k2mx+10k
,(10k2+6)x2-20k2mx+10k
设A(x1,y1)、B(x2,y2),则x1+x2= ,x1x2=
,x1x2=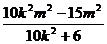 4分
4分
则xm=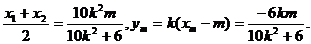 5分
5分
若存在k,使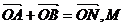 为ON的中点,∴
为ON的中点,∴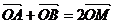 .
.
∴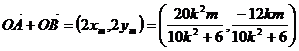 ,
,
即N点坐标为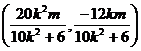 .
6分
.
6分
由N点在椭圆上,则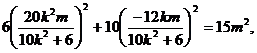 7分
7分
即5k4-2k2-3=0.∴k2=1或k2=-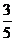 (舍).
(舍).
故存在k=±1使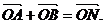 8分
8分
(Ⅱ)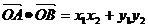 =x1x2+k2(x1-m)(x2-m)
=x1x2+k2(x1-m)(x2-m)
=(1+k2)x1x2-k
=(1+k2)? 10分
10分
由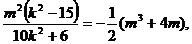 得
得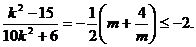 12分
12分
即k2-15≤-20k2-12,k2≤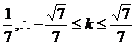 且k≠0. 14分
且k≠0. 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com