
2007年常州市初中毕业、升学统一考试
数 学
注意事项:1.全卷共8页,28题,满分120分,考试时间120分钟.
2.答卷前将密封线内的项目填写清楚,并将座位号填写在试卷规定的位置上.
3.用蓝色或黑色钢笔、圆珠笔将答案直接填写在试卷上.
4.考生在答题过程中,可以使用CZ1206,HY82型函数计算器,若试题计算结果没有要求取近似值,则计算结果取精确值(保留根号和 ).
).
一、填空题(本大题每个空格1分,共18分.把答案填在题中横线上)
1. 的相反数是
,
的相反数是
, 的绝对值是
,立方等于
的绝对值是
,立方等于 的数是 .
的数是 .
2.点 关于
关于 轴对称的点的坐标是 ;点
轴对称的点的坐标是 ;点 关于原点对称的点的坐标是 .
关于原点对称的点的坐标是 .
3.若 ,则
,则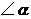 的余角是
°,
的余角是
°, .
.
4.在校园歌手大赛中,七位评委对某位歌手的打分如下:9.8,9.5,9.7,9.6,9.5,9.5,9.6,则这组数据的平均数是 ,极差是 .
5.已知扇形的半径为 ,则扇形的弧长是
cm,扇形的圆心角为
°.
,则扇形的弧长是
cm,扇形的圆心角为
°.
6.已知一次函数 的图象经过点
的图象经过点 ,
, ,则
,则 ,
, .
.
7.如图,已知 ,
,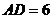 ,
, ,
, ,
, ,
,
则 °,
°, ,
, .
.

8.二次函数 的部分对应值如下表:
的部分对应值如下表:

…


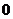

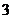

…

…

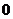

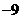


…
二次函数 图象的对称轴为
图象的对称轴为 ,
, 对应的函数值
对应的函数值 .
.
二、选择题(下列各题都给出代号为A,B,C,D的四个答案,其中有且只有一个是正确的,把正确答案的代号填在题后( )内,每小题2分,共18分)
9.在下列实数中,无理数是( )
A. B.
B. C.
C. D.
D.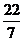
10.在函数 中,自变量
中,自变量 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. D.
D.
11.下列轴对称图形中,对称轴的条数最少的图形是( )
A.圆 B.正六边形 C.正方形 D.等边三角形
12.袋中有3个红球,2个白球,若从袋中任意摸出1个球,则摸出白球的概率是( )
A. B.
B.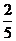 C.
C. D.
D.
13.如图,图象(折线 )描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( )
)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( )
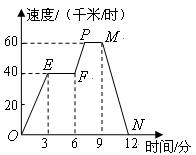
A.第3分时汽车的速度是40千米/时
B.第12分时汽车的速度是0千米/时
C.从第3分到第6分,汽车行驶了120千米
D.从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
14.下面各个图形是由6个大小相同的正方形组成的,其中能沿正方形的边折叠成一个正方体的是( )

15.小明和小莉出生于1998年12月份,他们的出生日不是同一天,但都是星期五,且小明比小莉出生早,两人出生日期之和是22,那么小莉的出生日期是( )
A.15号 B.16号 C.17号 D.18号
16.若二次函数 (
( 为常数)的图象如下,则
为常数)的图象如下,则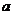 的值为( )
的值为( )
A. B.
B. C.
C. D.
D.
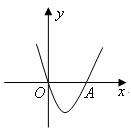
17.如图,在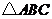 中,
中, ,
,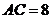 ,
,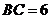 ,经过点
,经过点 且与边
且与边 相切的动圆与
相切的动圆与 分别相交于点
分别相交于点 ,则线段
,则线段 长度的最小值是( )
长度的最小值是( )

A.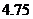 B.
B.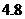 C.
C. D.
D.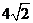
三、解答题(本大题共2小题,共18分.解答应写出演算步骤)
18.(本小题满分10分)化简:
(1) ;
(2)
;
(2) .
.
19.(本小题满分8分)解方程:
(1)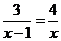 ;
(2)
;
(2) .
.
四、解答题(本大题共2小题,共12分.解答应写出证明过程)
20.(本小题满分5分)
已知,如图,在 中,
中, 的平分线交
的平分线交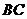 边于点
边于点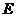 .
.
求证: .
.

21.(本小题满分7分)
已知,如图,延长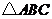 的各边,使得
的各边,使得 ,
, ,顺次连接
,顺次连接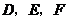 ,得到
,得到 为等边三角形.
为等边三角形.
求证:(1) ;
;
(2)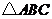 为等边三角形.
为等边三角形.

五、解答题(本大题共2小题,共15分.解答应写出文字说明或演算步骤)
22.(本小题满分7分)
图1是某市

(1)图2是该市
(2)在这10天中,最低气温的众数是 ,中位数是 ,方差是 .
23.(本小题满分8分)
 口袋中装有2个小球,它们分别标有数字
口袋中装有2个小球,它们分别标有数字 和
和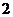 ;
; 口袋中装有3个小球,它们分别标有数字
口袋中装有3个小球,它们分别标有数字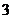 ,
,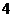 和
和 .每个小球除数字外都相同.甲、乙两人玩游戏,从
.每个小球除数字外都相同.甲、乙两人玩游戏,从 两个口袋中随机地各取出1个小球,若两个小球上的数字之和为偶数,则甲赢;若和为奇数,则乙赢.这个游戏对甲、乙双方公平吗?请说明理由.
两个口袋中随机地各取出1个小球,若两个小球上的数字之和为偶数,则甲赢;若和为奇数,则乙赢.这个游戏对甲、乙双方公平吗?请说明理由.
六、探究与画图(本大题共2小题,共13分)
24.(本小题满分6分)
如图,菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为 和
和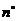 ,将菱形的“接近度”定义为
,将菱形的“接近度”定义为 ,于是,
,于是, 越小,菱形越接近于正方形.
越小,菱形越接近于正方形.
①若菱形的一个内角为 ,则该菱形的“接近度”等于
;
,则该菱形的“接近度”等于
;
②当菱形的“接近度”等于 时,菱形是正方形.
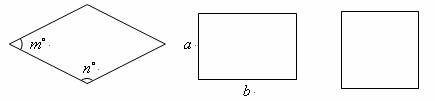
(2)设矩形相邻两条边长分别是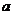 和
和 (
(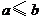 ),将矩形的“接近度”定义为
),将矩形的“接近度”定义为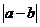 ,于是
,于是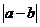 越小,矩形越接近于正方形.
越小,矩形越接近于正方形.
你认为这种说法是否合理?若不合理,给出矩形的“接近度”一个合理定义.
25.(本小题满分7分)
已知⊙ 经过
经过 ,
,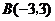 ,
, ,
,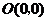 四点,一次函数
四点,一次函数 的图象是直线
的图象是直线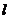 ,直线
,直线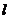 与
与 轴交于点
轴交于点 .
.
(1)在下面的平面直角坐标系中画出⊙ ,直线
,直线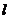 与⊙
与⊙ 的交点坐标为
;
的交点坐标为
;
(2)若⊙ 上存在整点
上存在整点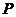 (横坐标与纵坐标均为整数的点称为整点),使得
(横坐标与纵坐标均为整数的点称为整点),使得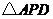 为等腰三角形,所有满足条件的点
为等腰三角形,所有满足条件的点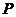 坐标为 ;
坐标为 ;
(3)将⊙ 沿
沿 轴向右平移
个单位时,⊙
轴向右平移
个单位时,⊙ 与
与 相切.
相切.

七、解答题(本大题共3小题,共26分.解答应写出文字说明、证明过程或演算步骤)
26.(本小题满分7分)
一等奖
二等奖
三等奖
1盒福娃和1枚徽章
1盒福娃
1枚徽章
用于购买奖品的总费用不少于1000元但不超过1100元,小明在购买“福娃”和微章前,了解到如下信息:
学校举办“迎奥运”知识竞赛,设一、二、三等奖共12名,奖品发放方案如下表:
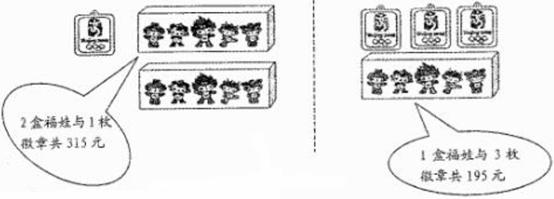
(1)求一盒“福娃”和一枚徽章各多少元?
(2)若本次活动设一等奖2名,则二等奖和三等奖应各设多少名?
27.(本小题满分9分)
已知,如图,正方形 的边长为6,菱形
的边长为6,菱形 的三个顶点
的三个顶点 分别在正方形
分别在正方形 边
边 上,
上, ,连接
,连接 .
.
(1)当 时,求
时,求 的面积;
的面积;
(2)设 ,用含
,用含 的代数式表示
的代数式表示 的面积;
的面积;
(3)判断 的面积能否等于
的面积能否等于 ,并说明理由.
,并说明理由.

28.(本小题满分10分)
已知 与
与 是反比例函数
是反比例函数 图象上的两个点.
图象上的两个点.
(1)求 的值;
的值;
(2)若点 ,则在反比例函数
,则在反比例函数 图象上是否存在点
图象上是否存在点 ,使得以
,使得以 四点为顶点的四边形为梯形?若存在,求出点
四点为顶点的四边形为梯形?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com