
2008年江苏省启东中学中考模拟考试(二)
数学试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分
第Ⅰ卷(选择题,共32分)
一、选择题(本题共10小题;第1~8题每小题3分,第9~10题每小题4分,共32分)下列各题都有代号为A、B、C、D的四个结论供选择,其中只有一个结论是正确的.
1.|-2|的值是 ( )
A.-2 B.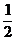 D.
D.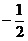
2.如图是一个正方体的展开图,将它折叠成正方体后,“建”字的对面是( )
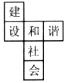
A.和 B.谐 C.社 D.会
3.下列运算中,正确的是 ( )
A.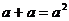 B.
B.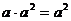
C.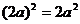 D.
D.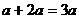
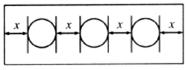
4.为了做一个试管架,在长为 cm(
cm( >6)的木板上钻3个小孔,如图所示,每个小孔的直径为
>6)的木板上钻3个小孔,如图所示,每个小孔的直径为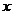 等于 ( )
等于 ( )
A.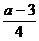 cm B.
cm B. cm C.
cm C.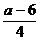 cm D.
cm D.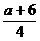 cm
cm
5.某城市2003年底已有绿化面积300hm2,经过两年绿化,绿化面积逐年增加,到2005年底增加到363hm2.设绿化面积平均每年的增长率为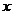 ,由题意,所列方程正确的是 ( )
,由题意,所列方程正确的是 ( )
A.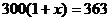 B.
B.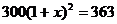
C.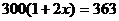 D.
D.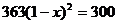
6.在平面直角坐标系中,若点P(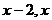 )在第二象限,则
)在第二象限,则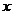 的取值范围为 ( )
的取值范围为 ( )
A.0<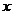 <2
B.
<2
B.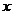 <
<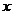 >0 D.
>0 D.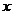 >2
>2
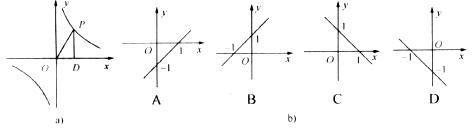
7.如图a所示,点P为反比例函数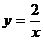 上的一动点,作PD⊥
上的一动点,作PD⊥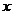 轴于点D,△POD的面积为k,则函数
轴于点D,△POD的面积为k,则函数 的图像为图b中的 ( )
的图像为图b中的 ( )
8.如图所示,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为 ( )
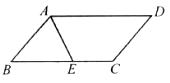
A.2和3 B.3和
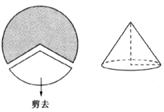
9.如图,如果从半径为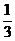 圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为 ( )
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为 ( )
A.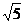 cm C.8cm D.5
cm C.8cm D.5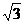 cm
cm
10.如图所示,直线AB,CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射 线OA上,且与点O的距离为6cm.如果⊙P以1cm/s的速度沿由A向B的方向移动,那么⊙P与直线CD相切时,⊙P运动了 ( )

A.4s B.8s C.4s或6s D.4s或8s
第Ⅱ卷(共118分)
二、填空题(本题共8小题;每小题3分,共24分)请把最后结果填在题中横线上.
11.分解因式: .
.
12.如图所示的围棋盘放在平面直角坐标系内,黑棋A的坐标为(-1,2),那么白棋B的坐标是 .

13.某农科院为了选出适合某地种植的甜玉米种子,对甲、乙两个品种甜米各用10块试验田进行试验,得到这两个品种甜玉米每公顷产量的两组数据(如图所示),根据图中的信息,可知存试验田中, 种甜玉米的产量比较稳定.

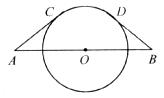
14.如图所示,AB= ,O为AB的中点,AC,BD都是半径为3的⊙O的切线,C,D切点,则
,O为AB的中点,AC,BD都是半径为3的⊙O的切线,C,D切点,则 的长为
.
的长为
.
15.如图,小“鱼”与大“鱼”是位似图形,已知小“鱼”上一个“顶点”的坐标为( ),那么大“鱼”上对应“顶点”的坐标为 .
),那么大“鱼”上对应“顶点”的坐标为 .

16.如图所示的抛物线是二次函数 的图像,那么
的图像,那么 的值是 .
的值是 .

17.小宇同学在一次手工制作活动中,先把一张矩形纸片按图a的方式进行折叠,使折 痕的左侧部分比右侧部分短1cm;展开后按图b的方式再折叠一次,使第二次折痕的左侧部分比右侧部分长1cm,再展开后,在纸上形成的两条折痕之间的距离是 cm.

18.用同样规格的黑白两种颜色的正方形瓷砖按图所示方式铺地板,则图c中有黑色瓷砖
块,第 个图形中需要黑色瓷砖 块(用含
个图形中需要黑色瓷砖 块(用含 的代数式表示).
的代数式表示).

三、解答题(本大题共10个小题;共94分.解答应写出文字说明、证明过程或演算步骤)
19.(本小题满分7分)计算:
20.(本小题满分8分)已知 ,求
,求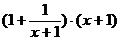 的值
的值
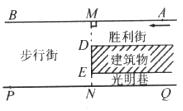
21.(本小题满分8分)如图所示,一段街道的两边缘所在直线分别为AB,PQ,并且AB//PQ.建筑物的一端DE所在的直线MN⊥AB于点M,交PQ于点N,小亮从胜利街的A处,沿着AB方向前进,小明一直站在点P的位置等候小亮.
(1)请你在图中画出小亮恰好能看见小明时的视线,以及此时小亮所在位置(用点C标出).
(2)已知:MN=20m,MD=8m,PN=24m,求(1)中的点C到胜利街口的距离CM.
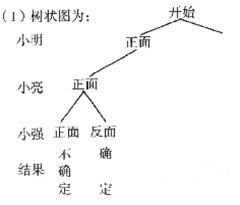
22.(本小题满分9分)小明、小亮和小强三人准备下象棋,他们约定用“抛硬币”的游戏方式来确定哪两个人先下棋,规则如图:

(1)请你完成下面表示游戏一个回合所有可能出现的结果的树状图.
(2)求一个回合能确定两人先下棋的概率.
23.(本题11分)某私立中学准备招聘教职员工60名,所有员工的月工资情况如下:
员工
管理人员
教学人员
人员结构
校长
副校长
部处主任
教研组长
高级教师
中级教师
初级教师
员工人数/人
1
2
4
10
3
每人月工资/元
20000
17000
2500
2300
2200
2000
900
请根据上面提供的信息,回答下列问题:
(1)如果学校准备招聘“高级教师”和“中级教师”共40名(其他员工人数不变),其中高级教师至少要招聘13人,而且学校对高级教师、中级教师的月支付工资不超过83000元,按学校要求,对高级教师、中级教师有几种招聘方案?
(2)(1)中的哪种方案对学校所支付的月工资最少?并说明理由.
(3)在学校所支付的月工资最少时,将上表补充完整,并求所有员工月工资的中位数和众数.
24.(本题6分)如图,菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为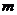 °和
°和 °,将菱形的“接近度”定义为
°,将菱形的“接近度”定义为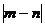 ,
于是,
,
于是,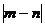 越小,菱形越接近于正方形.
越小,菱形越接近于正方形.
①若菱形的一个内角为70°,则该菱形的“接近度”等于
②当菱形的“接近度”等于 时,菱形是正方形.
(2)设矩形相邻两条边长分别是 和
和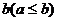 ,将矩形的“接近度”定义为
,将矩形的“接近度”定义为 ,于是
,于是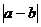 越小,矩形越接近于正方形.
越小,矩形越接近于正方形.
你认为这种说法是否合理?若不合理,给出矩形的“接近度”一个合理定义.
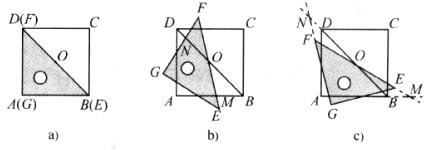
25.(本小题满分10分)如图a,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.
(1)如图b,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想;
(2)若三角尺GEF旋转到如图c所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
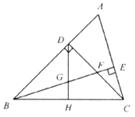
26.(本小题满分10分)已知:如图所示△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G.
(1)求证:BF=AC.
(2)求证:CE=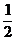 BF.
BF.
(3)CE与BG的大小关系如何?试证明你的结论.
27.(本小题满分12分)某茶厂种植“春蕊”牌绿茶,由历年来市场销售行情知道,从每年的3月25日起的180天内,绿茶市场销售单价y(元)与上市时间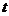 (天)的关系可以近似地用图a中的一条折线表示.绿茶的种植除了与气候、种植技术有关外,其种植的成本单价
(天)的关系可以近似地用图a中的一条折线表示.绿茶的种植除了与气候、种植技术有关外,其种植的成本单价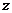 (元)与上市时间
(元)与上市时间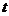 (天)的关系可以近似地用图b的抛物线表示.
(天)的关系可以近似地用图b的抛物线表示.
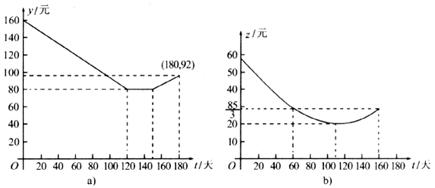
(1)直接写出图a中表示的市场销售单价y(元)与上市时间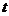 (天)(
(天)(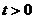 )的函数关系式.
)的函数关系式.
(2)求出图b中表示的种植成本单价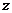 (元)与上市时间
(元)与上市时间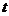 (天)(
(天)( 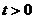 )的函数关系式.
)的函数关系式.
(3)认定市场销售单价减去种植成本单价为纯收益单价,问何时上市的绿茶纯收益单价最大?
(说明:市场销售单价和种植成本单价的单位:元/500g)
28.(本小题满分13分)如图a,一架长4m的梯子AB斜靠在与地面OM垂直的墙壁ON上,梯子与地面的倾斜角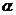 为60°.
为60°.
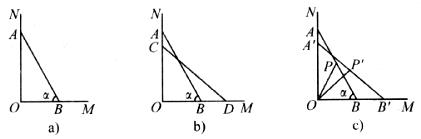
(1)求AO与BO的长;
(2)若梯子顶端A沿NO下滑,同时底端B沿OM向右滑行.
①如图b,设A点下滑到C点,B点向右滑行到D点,并且AC:BD=2:3,试计算梯子顶端A沿NO下滑多少米;
②如图c,当A点下滑到A’点,B点向右滑行到B’点时,梯子AB的中点P也随之运动到P’点.若∠POP’=15°,试求AA’的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com