
2008-2009学年度淄博市临淄区第二学期初四期中考试
数学试卷
说明:
1.同学们参加诊断检测的主要目的在于及时了解自己的学习情况,便于及时调整自己的学习策略和学习方法,为同学们的可持续学习打好基础.
2.本诊断检测试题共包含三个大题(总成绩满分120分)及附加题( 10分),检测时间120分钟.
一、选择题(本题共12小题,在每小题所给出的四个选项中,只有一个是正确的,请把正确的选项填在下面的表中.每小题3分,满分36分,错选、不选或选出的答案超过一个,均记0分.)
1.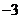 的倒数是
的倒数是
A.3
B.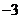 C.
C.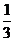 D.
D.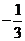
2.若梯形的面积为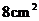 ,高为
,高为
A.
3.下列算式中,正确的是
A.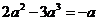 B.
B.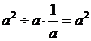
C. D.
D.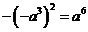
4.与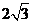 是同类二次根式的是
是同类二次根式的是
A.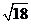 B.
B.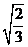 C.
C.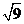 D.
D.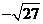
5.袋中放有一套(五枚)北京2008年奥运会吉祥物福娃纪念币,依次取出(不放回)两枚纪念币,恰好能够组成“欢迎”的概率是
A.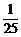 B.
B.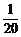 C.
C.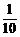 D.
D.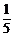

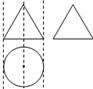
6.图中三视图所对应的直观图是
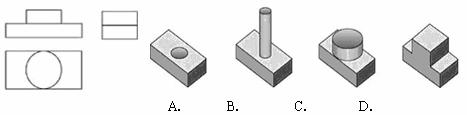
7.如图,下列分子结构模型平面图中,既是轴对称图形又是中心对称图形的个数是

A.4个 B.3个 C.2个 D.1个
8.在平面直角坐标系中,若点P(m-3,m+1)在第二象限,则m的取值范围为
A.-1<m<3 B.m>
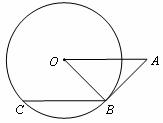
9.如下图,A是半径为2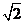 的⊙O外一点,OA=4,AB是⊙O的切线,点B是切点,弦BC∥OA,则BC的长为
的⊙O外一点,OA=4,AB是⊙O的切线,点B是切点,弦BC∥OA,则BC的长为
A.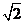 B.
B.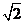 D.4
D.4
10.如果点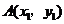 和点
和点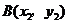 是直线
是直线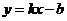 上的两点,且当
上的两点,且当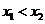 时,
时,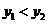 ,那么函数
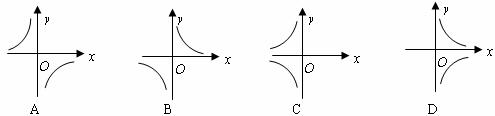
,那么函数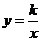 的图象大致是
的图象大致是
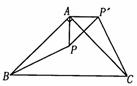
11.如下图,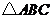 是等腰直角三角形,
是等腰直角三角形,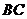 是斜边,将
是斜边,将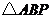 绕点
绕点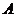 逆时针旋转后,能与
逆时针旋转后,能与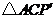 重合,如果
重合,如果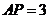 ,那么
,那么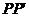 的长等于
的长等于
A.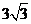 B.
B.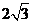 C.
C. D.
D.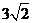
12.一个质点在第一象限及x轴、y轴上运动.在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动?即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…?,且每秒移动一个单位,那么第35秒时质点所在位置的坐标是
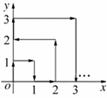
A.(4,0) B.(5,0) C.(0,5) D.(5,5)
二、填空题(本大题共5个小题,每小题4分,满分20分)
13.国家游泳中心――“水立方”是2008年北京奥运会标志性建筑物之一,其工程占地面积为
14.如图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么这个几何体的侧面积是 .
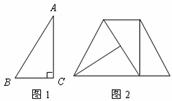
15.如图1,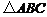 是直角三角形,如果用四张与
是直角三角形,如果用四张与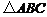 全等的三角形纸片恰好拼成一个等腰梯形,如图2,那么在
全等的三角形纸片恰好拼成一个等腰梯形,如图2,那么在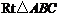 中,
中,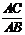 的值是 .
的值是 .
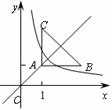
16.如图:等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线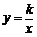 (k≠0)与
(k≠0)与 有交点,则k的取值范围是 .
有交点,则k的取值范围是 .
17.AB是⊙O的直径,弦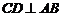 于E,如果
于E,如果 cm,
cm,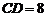 cm,那么AE的长为
.
cm,那么AE的长为
.
三、解答题:本大题共7小题,第18题6分,第19题8分,第20、21、22、23、24题每题10分,共64分.解答要写出必要的文字说明、证明过程或演算步骤.
18.先化简,再求值:
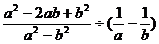 ,其中
,其中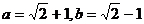 .
.
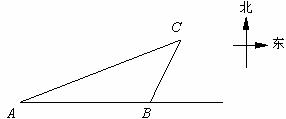
19.一艘轮船自西向东航行,在A处测得东偏北21.3°方向有一座小岛C,继续向东航行
(参考数据:sin21.3°≈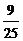 ,tan21.3°≈
,tan21.3°≈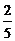 ,
sin63.5°≈
,
sin63.5°≈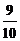 ,tan63.5°≈2)
,tan63.5°≈2)
20.为了进一步了解八年级学生的身体素质情况,体育老师对八年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
组别
次数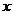
频数(人数)
第1组
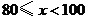
第2组
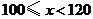

第3组
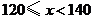
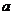
第4组
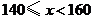
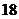
第5组
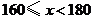
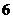
请结合图表完成下列问题:
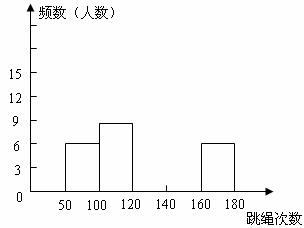
(1)表中的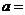 ;
;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第 组;
(4)若八年级学生一分钟跳绳次数(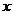 )达标要求是:
)达标要求是: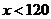 不合格;
不合格;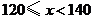 为合格;
为合格;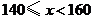 为良;
为良;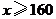 为优.根据以上信息,请你给学校或八年级同学提一条合理化建议: .
为优.根据以上信息,请你给学校或八年级同学提一条合理化建议: .
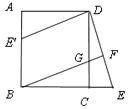
21.已知:如图,在正方形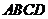 中,
中,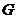 是
是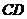 上一点,延长
上一点,延长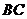 到
到 ,使
,使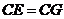 ,连接
,连接 并延长交
并延长交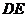 于点
于点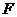 .
.
(1)求证: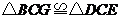 ;
;
(2)将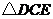 绕点
绕点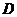 顺时针旋转
顺时针旋转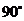 得到
得到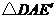 ,判断四边形
,判断四边形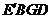 是什么特殊四边形?并说明理由.
是什么特殊四边形?并说明理由.
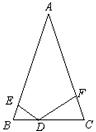
22.如图,在△ABC 中,AB=AC,D是BC边上的一点,DE⊥AB,DF⊥AC,垂足分别为E、F,
(1)添加一个条件,使DE= DF,并说明理由.
(2)请你猜想DE+DF与腰上的高有怎样的大小关系?并证明你猜想的结论.
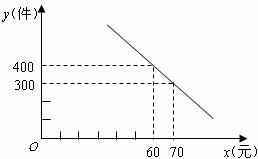
23.某服装公司试销一种成本为每件50元的T恤衫,规定试销时的销售单价不低于成本价,又不高于每件70元,试销中销售量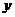 (件)与销售单价
(件)与销售单价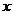 (元)的关系可以近似的看作一次函数(如图)。
(元)的关系可以近似的看作一次函数(如图)。
(1)求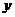 与
与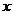 之间的函数关系式;
之间的函数关系式;
(2)设公司获得的总利润(总利润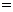 总销售额
总销售额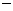 总成本)为
总成本)为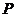 元,求
元,求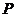 与
与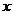 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量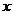 的取值范围;根据题意判断:当
的取值范围;根据题意判断:当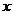 取何值时,
取何值时,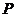 的值最大?最大值是多少?
的值最大?最大值是多少?
24.小明在复习数学知识时,针对“求一元二次方程的解”,整理了以下的几种方法,请你按有关内容补充完整:
复习日记卡片
内容:一元二次方程解法归纳 时间:2008年6月×日
举例:求一元二次方程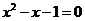 的两个解
的两个解
方法一:选择合适的一种方法(公式法、配方法、分解因式法)求解
解方程: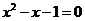 .
.
解:
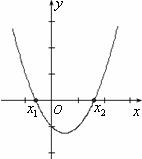
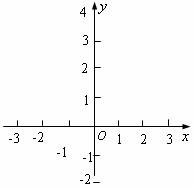
方法二:利用二次函数图象与坐标轴的交点求解
如图所示,把方程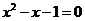 的解看成是二次函数
的解看成是二次函数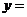 的图象与
的图象与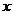 轴交点的横坐标,即
轴交点的横坐标,即 就是方程的解.
就是方程的解.
方法三:利用两个函数图象的交点求解
(1)把方程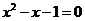 的解看成是一个二次函数
的解看成是一个二次函数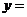 的图象与一个一次函数
的图象与一个一次函数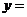 图象交点的横坐标;
图象交点的横坐标;
(2)画出这两个函数的图象,用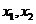 在
在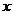 轴上标出方程的解.
轴上标出方程的解.
附加题(满分10分)
已知:抛物线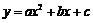 (a≠0),顶点C (1,
(a≠0),顶点C (1,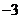 ),与x轴交于A、B两点,
),与x轴交于A、B两点,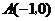 .
.
(1)求这条抛物线的解析式.
(2)如图,以AB为直径作圆,与抛物线交于点D,与抛物线对称轴交于点E,依次连接A、D、B、E,点P为线段AB上一个动点(P与A、B两点不重合),过点P作PM⊥AE于M,PN⊥DB于N,请判断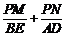 是否为定值? 若是,请求出此定值;若不是,请说明理由.
是否为定值? 若是,请求出此定值;若不是,请说明理由.
(3)在(2)的条件下,若点S是线段EP上一点,过点S作FG⊥EP ,FG分别与边AE、BE相交于点F、G(F与A、E不重合,G与E、B不重合),请判断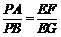 是否成立.若成立,请给出证明;若不成立,请说明理由.
是否成立.若成立,请给出证明;若不成立,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com