
2009年内江市高中阶段教育学校招生考试及初中毕业会考
数 学
(本试卷满分150分,考试时间120分钟)
会考卷(共100分)
第Ⅱ卷(选择题 共36分)
一、选择题(本大题共l2小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.汽车向东行驶
A.
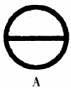
2.下列几个图形是国际通用的交通标志,其中不是中心对称图形的是 ( )



3.抛物线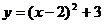 的顶点坐标是 ( )
的顶点坐标是 ( )
A.(2,3) B.(-2,3) C.(2,-3) D.(-2,-3)
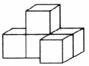
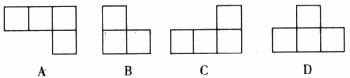
4.如图是由5个大小相同的正方体摆成的立体图形,它的正视图是 ( )
5.今年我国发现的首例甲型H1N1流感确诊病例在成都某医院隔离观察,要掌握他在一周内的体温是否稳定,则医生需了解这位病人7天体温的 ( )
A.众数 B.方差 C.平均数 D.频数
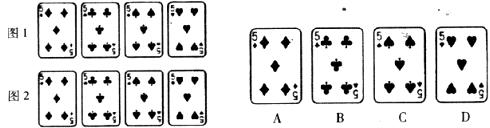
6.已知如图1所示的四张牌,若将其中一张牌旋转l80°后得到图2,则旋转的牌是( )
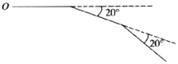
7.如图,小陈从O点出发,前进
A.
8.在边长为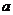 的正方形中挖去一个边长为
的正方形中挖去一个边长为 的小正方形(
的小正方形(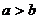 )(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证 ( )
)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证 ( )

A.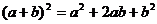 B.
B.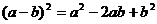
C. D.
D.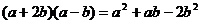
9.打开某洗衣机开关(洗衣机内无水),在洗涤衣服时,洗衣机经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量 (升)与时间
(升)与时间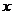 (分钟)之间满足某种函数关系,其函数图象大致为 ( )
(分钟)之间满足某种函数关系,其函数图象大致为 ( )
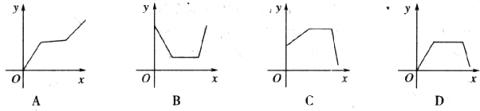
10.如图所示,数轴上表示2,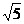 的对应点分别为C,B,点C是AB的中点,则点A表示的数是 ( )
的对应点分别为C,B,点C是AB的中点,则点A表示的数是 ( )
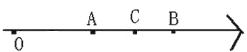
A.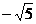 B.
B.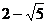 C.
C.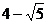 D.
D.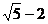
11.若关于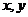 的方程组
的方程组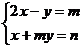 的解是
的解是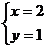 ,则
,则 为
( )
为
( )
A.1 B.
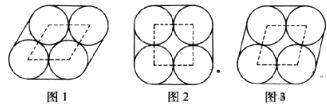
12.在校运动会上,三位同学用绳子将四根同样大小的接力棒分别按横截面如图1、图2、图3所示的方式进行捆绑,三个图中的四个圆心的连线(虚线)分别构成菱形、正方形、菱形,如果把三种方式所用绳子的长度分别用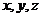 来表示,则
( )
来表示,则
( )
A. B.
B.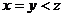 C.
C.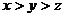 D.
D.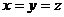
第Ⅱ卷(非选择题 共64分)
二、填空题(本大题共4小题,每小题5分,共20分。请把答案填在题中横线上)
13.记者从2009年5月7日上午四川省举行的“5?12”抗震救灾周年新闻发布会上了解到,经过多方不懈努力,四川已帮助近l 300 000名受灾群众实现就业.l 300 000 用科学记数法表示为_______________.
14.分解因式: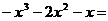 _____________.
_____________.
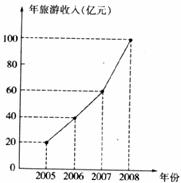
15.某人为了了解他所在地区的旅游情况,收集了该地区2005年至2008年每年旅游收入的有关数据,整理并绘成图.根据图中信息,可知该地区2005年至2008年四年的年旅游平均收入是________________亿元.
16.如图,梯形ABCD中,AD//BC,两腰BA与CD的延长线相交于P,PF⊥BC,AD=2,BC=5,EF=3,则PF=____________.

三、解答题(本大题共5小题,共44分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分6分)
计算: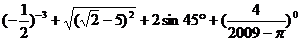 .
.
18.(本小题满分9分)
如图,已知AB=AC,AD=AE,求证:BD=CE。
19.(本小题满分9分)
有形状、大小和质地都相同的四张卡片,正面分别写有A,B,C,D和一个等式,将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
A: B:
B: C:
C: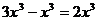 D:
D: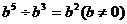
(1)用画树状图或列表的方法表示抽取两张卡片可能出现的所有情况(结果用A,B,C,D表示);
(2)小明和小强按下面规则做游戏:抽取的两张卡片上若等式都不成立,则小明胜,若至少有一个等式成立,则小强胜.你认为这个游戏公平吗?若公平,请说明理由;若不公平,则这个规则对谁有利,为什么?
20.(本小题满分10分)
某服装厂为学校艺术团生产一批演出服,总成本3 200元,售价每套40元。服装厂向25名家庭贫困学生免费提供。经核算,这25套演出服的成本正好是原定生产这批演出服的利润.问这批演出服生产了多少套?
21.(本小题满分10分)
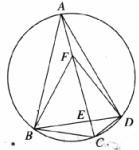
如图,四边形ABCD内接于圆,对角线AC与BD相交于点E,F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC.求证:
(1)CD⊥DF;
(2)BC=2CD.
加试卷(共50分)
一、填空题(本大题共4小题,每小题5分,共20分。请把答案填在题中横线上)
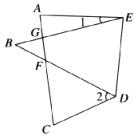
1.如图所示,将△ABC沿着DE翻折,若∠1+∠2=80°,则∠B=__________.
2.已知Rt△ABC的周长是4+4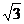 ,斜边上的中线长是2,则S△ABC=_________.
,斜边上的中线长是2,则S△ABC=_________.
3.已知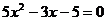 ,则
,则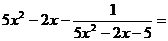 _______________
_______________
4.把一张纸片剪成4块,再从所得的纸片中任取若干块,每块又剪成4块,像这样依次地进行下去,到剪完某一次为止,那么2007,2 008,2 009,2 010这四个数中_________可能是剪出的纸片数.
二、解答题(本大题共3小题,共30分.解答应写出文字说明、证明过程或演算步骤)
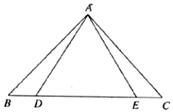
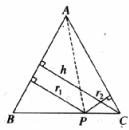
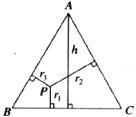
如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为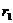 ,
, ,腰上的高为
,腰上的高为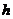 ,连接AP,则S△ABP+S△ACP=S△ABC,即:
,连接AP,则S△ABP+S△ACP=S△ABC,即: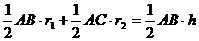
∴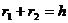 (定值).
(定值).
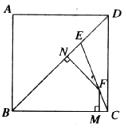
(1)理解与应用
如图,在边长为3的正方形ABCD中,点E为对角线BD上的一点,且BE=BC,F为CE上一点,FM⊥BC于M,FN⊥BD于N,试利用上述结论求出FM+FN的长.
(2)类比与推理
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:
已知等边△ABC内任意一点P到各边的距离分别为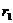 ,
, ,
,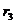 ,等边△ABC的高为
,等边△ABC的高为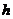 ,试证明:
,试证明: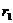 +
+ +
+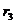 =
=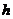 (定值)。
(定值)。
(3)拓展与延伸
若正 边形A1A2…A
边形A1A2…A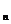 内部任意一点P到各边的距离为
内部任意一点P到各边的距离为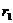 ,
, ,…,
,…,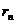 ,请问
,请问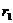 +
+ +…+
+…+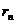 是否为定值,如果是,请合理猜测出这个定值。
是否为定值,如果是,请合理猜测出这个定值。
6.(本小题满分10分)
我市部分地区近年出现持续干旱现象,为确保生产生活用水,某村决定由村里提供一点,村民捐一点的办法筹集资金维护和新建一批储水池。该村共有243户村民,准备维护和新建的储水池共有20个,费用和可供使用的户数及用地情况如下表:
储水池
费用(万元/个)
可供使用的户数(户/个)
占地面积(m2/个)
新建
4
5
4
维护
3
18
6
已知可支配使用土地面积为106m2,若新建储水池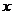 个,新建和维护的总费用为
个,新建和维护的总费用为 万元.
万元.
(1)求 与
与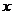 之间的函数关系;
之间的函数关系;
(2)满足要求的方案各有几种;
(3)若平均每户捐2 000元时:村里出资最多和最少分别是多少?
7.(本小题满分10分)
如图所示,已知点A(-l,0),B(3,0),C(0,t),且t>0,tan∠BAC=3,抛物线经过A,B,C三点,点P(2,m)是抛物线与直线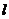 :
: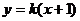 的一个交点.
的一个交点.
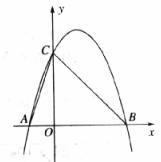
(1)求抛物线的解析式;
(2)对于动点Q(1,n),求PQ+QB的最小值;
(3)若动点M在直线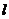 上方的抛物线上运动,求△AMP的边AP上的高
上方的抛物线上运动,求△AMP的边AP上的高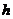 的最大值.
的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com