注 意 事 项
考生在答题前认真阅读本注意事项及各题答题要求
1.本斌卷共4页,包含填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分160分,考试时间为120分钟.考试结束后,请将本试卷和答题纸一并交回.
2.答题前,请您务必将自己的姓名、考试证号用书写黑色字迹的0.5毫米签字笔填写在试卷及答题纸上.
3.作答时必须用书写黑色字迹的0.5毫米签字笔写在答题纸上的指定位置,在其它位;置作答一律无效.
4.如有作图需要,可用2B铅笔作答,并请加黑加粗,描写清楚.
一、填空题:本大题共14题,每小题5分,共70分.请把答案填写在答题纸相应位置上.
试题详情
试题详情
2.若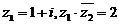 ,则
,则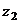 =
=
试题详情
3.一个容器的外形是一个棱长为2的正方体,其三视图
如图所示,则容器的容积为
试题详情
试题详情
的外接圆的直径为20,则实数
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
10.下列程序运行结果为
i←1
While i<7
i←i+2
s←2i+3
End While
Print s
End
试题详情
试题详情
试题详情
试题详情
试题详情
二、解答题:本大题共6小题,共计90分.解答时应写出文字说明、证明过程或演算步骤
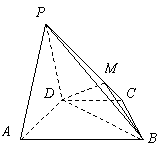 15. (本小题共14分)
15. (本小题共14分)
试题详情
试题详情
试题详情
试题详情
(Ⅲ)求四棱锥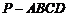 的体积.
的体积.
试题详情
试题详情
试题详情
试题详情
求不等式f(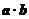 )>f(
)>f(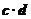 )的解集.
)的解集.
试题详情
试题详情
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量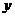 (升)关于行驶速度
(升)关于行驶速度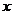 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: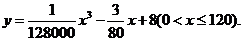 已知甲、乙两地相距100千米。
已知甲、乙两地相距100千米。
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
(1) 求函数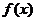 的解析式;
的解析式;
试题详情
试题详情
(3) 在(2)的条件下, 若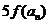 是
是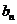 与
与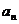 的等差中项, 试问数列
的等差中项, 试问数列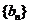 中第几项的值最小? 求出这个最小值.
中第几项的值最小? 求出这个最小值.
试题详情
试题详情
试题详情
(1)求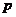 与
与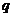 的关系;
的关系;
试题详情
(2)若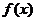 在其定义域内为单调函数,求
在其定义域内为单调函数,求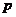 的取值范围;
的取值范围;
试题详情
(3)设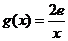 ,若在
,若在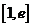 上至少存在一点
上至少存在一点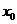 ,使得
,使得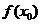 >
>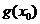 成立,求实数
成立,求实数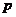 的取值范围.
的取值范围.
江苏省2009届高三南京市高考预测卷
试题详情
1. {2,8} 2.  3.
3.  4.
4. 
5. 
 6. 1 7.20
6. 1 7.20
8.  9.
9.  10.2
10.2
11. 12.
12.  13. [2,3] 14.
13. [2,3] 14. 
15.证明:(Ⅰ)在 中,
中,
∵ ,
, ,
, ,∴
,∴ .
.
∴ .????????????????? 2分
.????????????????? 2分
又 ∵平面 平面
平面 ,
,
平面 平面
平面 ,
, 平面
平面 ,
,
∴ 平面
平面 .
.
又 平面
平面 ,
,
∴平面 平面
平面 .………………………………………………………………4分
.………………………………………………………………4分
(Ⅱ)当 点位于线段PC靠近C点的三等分点处时,
点位于线段PC靠近C点的三等分点处时, 平面
平面 .………5分
.………5分
证明如下:连接AC,交 于点N,连接MN.
于点N,连接MN.
∵ ,所以四边形
,所以四边形 是梯形.
是梯形.
∵ ,∴
,∴ .
.
又 ∵ ,
,
∴
 ,∴
,∴ MN.…………………………………………………7分
MN.…………………………………………………7分
∵ 平面
平面 ,∴
,∴ 平面
平面 .………………………………………9分
.………………………………………9分
(Ⅲ)过 作
作 交
交 于
于 ,
,
∵平面 平面
平面 ,
,
∴ 平面
平面 .
.
即 为四棱锥
为四棱锥 的高.……………………………………………………11分
的高.……………………………………………………11分
又 ∵ 是边长为4的等边三角形,∴
是边长为4的等边三角形,∴ .……………12分
.……………12分
 在
在 中,斜边
中,斜边 边上的高为
边上的高为 ,此即为梯形
,此即为梯形 的高.
的高.
∴梯形 的面积
的面积 .
.
故 .……………………………………………14分
.……………………………………………14分
16.设 的二次项系数为
的二次项系数为 ,其图象上两点为(
,其图象上两点为( ,
, )、B(
)、B( ,
, )因为
)因为 ,
, ,所以
,所以 ,由x的任意性得f(x)的图象关于直线x=1对称, ………………………………………………………………(2分)
,由x的任意性得f(x)的图象关于直线x=1对称, ………………………………………………………………(2分)
∵  ,
, ,
, ,
,
 ,
, ,
,
 ,………………………………(4分)
,………………………………(4分)
∴ 当 时,∵f(x)在x≥1内是增函数,
时,∵f(x)在x≥1内是增函数,





 ,
, .
.
∵  , ∴
, ∴  .………………………………………………(8分)
.………………………………………………(8分)
当 时,∵f(x)在x≥1内是减函数.
时,∵f(x)在x≥1内是减函数.
同理可得 或
或 ,
, .………………………………………(11分)
.………………………………………(11分)
综上: 的解集是当
的解集是当 时,为
时,为
当 时,为
时,为 ,或
,或 .
.
17.解:(1)若 千米/小时,每小时耗油量为
千米/小时,每小时耗油量为 升/小时. 共耗油
升/小时. 共耗油 升.
升.
所以,从甲地到乙地要耗油17.5升.
(2)设当汽车以 千米/小时的速度匀速行驶时耗油量最少,
千米/小时的速度匀速行驶时耗油量最少, ,耗油量为S升.
,耗油量为S升.
则 ,
,
 ,
,
令 ,解得,
,解得, .
.
列表:











单调减
极小值11.25
单调增

所以,当汽车以80千米/小时的速度匀速行驶时,耗油量最少,为11.25升.
18.解:(Ⅰ)设

对称轴方程 ,由题意
,由题意 或
或 或
或
∴ 或
或 或
或 ∴
∴
(Ⅱ)由已知与(Ⅰ)得: ,
, ,
,
 ,
, ,
, .
.
 椭圆的标准方程为
椭圆的标准方程为 .
.
设 ,
, ,联立
,联立
得 ,
,

又 ,
,
因为椭圆的右顶点为 ,
, ,即
,即 ,
,
 ,
,
 ,
, .
.
解得: ,
, ,且均满足
,且均满足 ,
,
当 时,
时, 的方程为
的方程为 ,直线过定点
,直线过定点 ,与已知矛盾;
,与已知矛盾;
当 时,
时, 的方程为
的方程为 ,直线过定点
,直线过定点 .
.
所以,直线 过定点,定点坐标为
过定点,定点坐标为 .
.
19. 解: (1) 由题知:  , 解得
, 解得 , 故
, 故 .
.
(2)  ,
,
 ,
,
 ,
,
又 满足上式. 所以
满足上式. 所以 .
.
(3) 若 是
是 与
与 的等差中项, 则
的等差中项, 则 ,
,
从而 , 得
, 得 .
.
因为 是
是 的减函数, 所以
的减函数, 所以
当 , 即
, 即 时,
时,  随
随 的增大而减小, 此时最小值为
的增大而减小, 此时最小值为 ;
;
当 , 即
, 即 时,
时,  随
随 的增大而增大, 此时最小值为
的增大而增大, 此时最小值为 .
.
又 , 所以
, 所以 ,
,
即数列 中
中 最小, 且
最小, 且 .
.
20. 解:(1)由题意得

而 ,所以
,所以 、
、 的关系为
的关系为
(2)由(1)知 ,
,

令 ,要使
,要使 在其定义域
在其定义域 内是单调函数,只需
内是单调函数,只需 在
在 内满足:
内满足: 恒成立.
恒成立.
①当 时,
时, ,因为
,因为 >
> ,所以
,所以 <0,
<0, <0,
<0,
∴ 在
在 内是单调递减函数,即
内是单调递减函数,即 适合题意;
适合题意;
②当 >0时,
>0时, ,其图像为开口向上的抛物线,对称轴为
,其图像为开口向上的抛物线,对称轴为 ,∴
,∴ ,
,
只需 ,即
,即 ,
,
∴ 在
在 内为单调递增函数,故
内为单调递增函数,故 适合题意.
适合题意.
③当 <0时,
<0时, ,其图像为开口向下的抛物线,对称轴为
,其图像为开口向下的抛物线,对称轴为 ,只要
,只要 ,即
,即 时,
时, 在
在 恒成立,故
恒成立,故 <0适合题意.
<0适合题意.
综上所述, 的取值范围为
的取值范围为 .
.
(3)∵ 在
在 上是减函数,
上是减函数,
∴ 时,
时, ;
; 时,
时, ,即
,即 ,
,
①当 时,由(2)知
时,由(2)知 在
在 上递减
上递减 <2,不合题意;
<2,不合题意;
②当0< <1时,由
<1时,由 ,
,
又由(2)知当 时,
时, 在
在 上是增函数,
上是增函数,
∴ <
< ,不合题意;
,不合题意;
③当 时,由(2)知
时,由(2)知 在
在 上是增函数,
上是增函数, <2,又
<2,又 在
在 上是减函数,
上是减函数,
故只需 >
> ,
, ,而
,而 ,
,
