
回归卷之三角函数――必修四、五
一、三角函数的定义
1、已知 ,在终边
,在终边 上取异于原点O的点P,则
上取异于原点O的点P,则 ______________.
______________.
2、已知 ,
, 在第三象限,
在第三象限, ______________.
______________.
3、在复平面内,O为坐标原点, 对应的复数为3+4i,
对应的复数为3+4i, 绕着O逆时针方向旋转
绕着O逆时针方向旋转 得到向量
得到向量 ,此向量对应复数是( )
,此向量对应复数是( )
4、必修四P126――3 , P25――4
二、平方关系
1、如果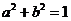 ,求
,求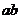 的范围______________,
的范围______________,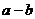 的范围_________________,
的范围_________________,
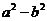 的范围______________,
的范围______________,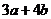 的范围______________.
的范围______________.
2、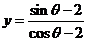 的值域______________
的值域______________
3、已知 ,求
,求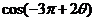 =______________
=______________
4、曲线C的参数方程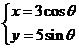 ,P(x,y)为C上的任意一点,A(0,-4),B(0,4)则
,P(x,y)为C上的任意一点,A(0,-4),B(0,4)则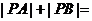 ______________.
______________.
5、必修四P157――B组5
三、三角变换
1、理清公式之间联系,P153――例2
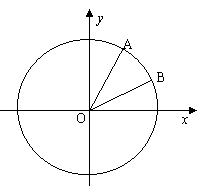 2、必修五P9――解三角形的进一步讨论;P11B组――1 P21练习3
2、必修五P9――解三角形的进一步讨论;P11B组――1 P21练习3
四、基本题型
1、如图,在平面直角坐标系xoy中,以ox轴为始边做两个锐角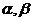 ,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为
,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为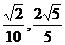
(1)求 的值; (2)求
的值; (2)求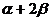 的值。
的值。
2、如图,已知点 点
点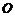 为坐标原点,点
为坐标原点,点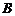 在第二象限,且
在第二象限,且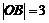 ,记
,记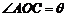 .
. 学科网
学科网
 (Ⅰ)求
(Ⅰ)求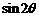 的值;
的值; 学科网 (Ⅱ)若
学科网 (Ⅱ)若 学科
学科 ,求
,求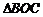 的面积.
的面积.
3、已知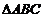 中,
中,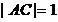 ,
,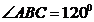 ,
,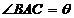 ,记
,记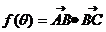 ,
,
(1)求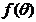 关于
关于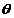 的表达式;(2)求
的表达式;(2)求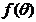 的值域;
的值域;
4、.若sinx+siny=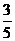 ,cosx+cosy=
,cosx+cosy=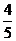
(1)求cos(x+y)的值;
(2)求cosx?cosy的值。
答案:四:1 (1)-3 (2)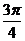 2(1)
2(1)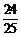 (2)
(2)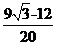 3 (2)
3 (2)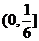
4 (1)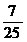 (2)-
(2)-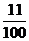
回归卷之平面向量(必修四)
一、回答下列式子的几何意义
1、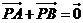
2、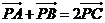
3、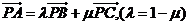
4、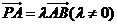
5、在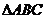 中,
中,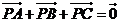
6、在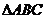 中,
中,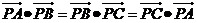
7、在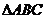 中,
中,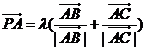
8、四边形ABCD,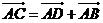
9、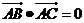
10、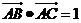
11、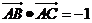
二、两个向量的数量积与两个向量共线
1、两个向量夹角的取值范围______________。在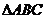 中,A、B、C成等差数列,
中,A、B、C成等差数列,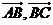 的夹角是______________。
的夹角是______________。
2、已知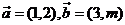
①如果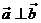 ,m=( ), ②如果
,m=( ), ②如果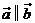 ,m=( )
,m=( )
③如果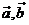 的夹角为锐角,m的范围是( ) ④如果
的夹角为锐角,m的范围是( ) ④如果 ,m=( )
,m=( )
⑤如果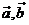 可作为平面向量的基底,m的范围是( )
可作为平面向量的基底,m的范围是( )
⑥与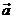 垂直的单位向量的坐标是______________.
垂直的单位向量的坐标是______________.
3、已知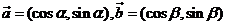 ①如果
①如果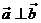 ,
,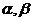 的关系是___________。②如果
的关系是___________。②如果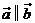 ,
,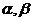 的关系是______________。
的关系是______________。
③如果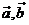 的夹角为
的夹角为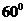 ,
,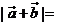 ( ),
( ),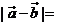 ( ),直线
( ),直线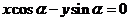 与圆
与圆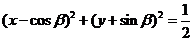 的位置关系是( )
的位置关系是( )
课本必修四P151B组4, P157B组4,P120,4
三、基本题型
1、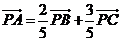 ,
,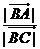 =______________.
=______________.
2、用向量知识回答下列问题:
①四边形ABCD为矩形的充要条件是______________ ②四边形ABCD为菱形的充要条件是______________―
3、已知点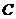 为
为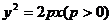 的准线与
的准线与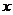 轴的交点,点
轴的交点,点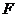 为焦点,点
为焦点,点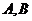 为抛物线上两个点,若
为抛物线上两个点,若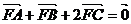 ,则向量
,则向量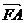 与
与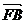 的夹角为
。
的夹角为
。
4、已知平面上不共线的四点O,A,B,C.若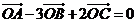 ,则
,则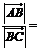 ___ .
___ .
5、设i,j分别是x轴、y轴正方向上的单位向量,且 = 4i-2j,
= 4i-2j,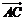 =7i+4j,
=7i+4j,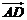 =3i+6j,则四边形ABCD的面积是________ .
=3i+6j,则四边形ABCD的面积是________ .
6、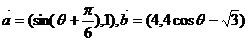 ,若
,若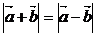 ,则
,则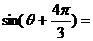 ( )
( )
A. 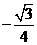 B.
B.
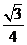 C.
C.
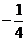 D.
D. 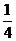
7、过点P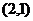 的直线与抛物线
的直线与抛物线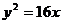 交于
交于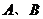 两点,且
两点,且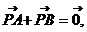 则此直线的方程为___________
则此直线的方程为___________
8.在空间直角坐标系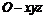 中,过点
中,过点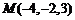 作直线
作直线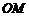 的垂线
的垂线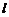 ,则直线
,则直线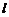 与平面
与平面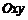 的交点
的交点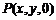 的坐标满足条件
( )
的坐标满足条件
( )
A.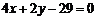 B.
B.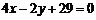
C. D.
D.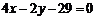
9、已知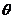 是
是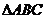 的最大内角,
的最大内角,
(1)向量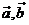 是否共线?说明理由
是否共线?说明理由
(2)定义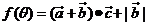 ,求
,求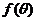 的最大值.
的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com