
2009最有影响力高考复习题(数学)1(3+3+4)
文博浪花工作室王培博推荐(
一、选择题:
1、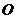 是△ABC所在平面内一点,且满足
是△ABC所在平面内一点,且满足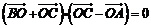 ,
,
则△ABC一定是 ( )答D
A.等边三角形 B.斜三角形 C.等腰直角三角形 D.直角三角形
2、在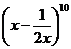 的展开式中,
的展开式中,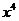 的系数为( ) 答C
的系数为( ) 答C
A. B.
B.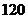 C.
C.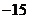 D.
D.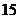
3、设F1,F2分别是双曲线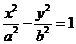 的左、右焦点。若双曲线上存在点A,使∠F1AF2=90º,且|AF1|=3|AF2|,则双曲线离心率为( ) 答B
的左、右焦点。若双曲线上存在点A,使∠F1AF2=90º,且|AF1|=3|AF2|,则双曲线离心率为( ) 答B
A.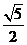 B.
B.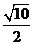 C.
C. 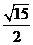 D.
D. 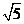
二、填空题:
4、在一个小组中有8名女同学和4名男同学,从中任意地挑选2名同学担任交通安全宣传志愿者,那么选到的两名都是女同学的概率是______(结果用分数表示)。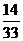
5、正四棱锥侧面与底面所成的角为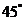 ,则其侧棱与底面所成的角为 .
,则其侧棱与底面所成的角为 .
6、给出下列四个函数:①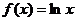 ;②
;②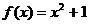 ;③
;③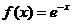 ;④
;④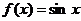 ,其中满足:“对任意
,其中满足:“对任意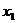 、
、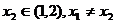 ,不等式
,不等式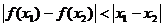 总成立”的是
。(将正确的序中与填在横线上)答:
总成立”的是
。(将正确的序中与填在横线上)答: ①③④
①③④
三、解答题:
7、(本题满分12分)投掷飞碟的游戏中,飞碟投入红袋记2分,投入蓝袋记1分,未投入袋记0分.现知某人在以前投掷1000次的试验中,有500次入红袋,250次入蓝袋,其余不能入袋
(Ⅰ)求该人在4次投掷中恰有三次投入红袋的概率;
(Ⅱ) 求该人两次投掷后得分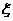 的数学期望.
的数学期望.
8、(本题满分14分)长方体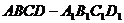 中,
中,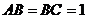 ,
,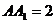 ,
,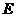 是侧棱
是侧棱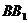 中点.
中点.
(Ⅱ)求二面角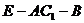 的大小;
的大小;
(Ⅲ)求三棱锥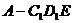 的体积.
的体积.
9、已知函数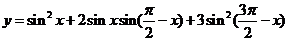 .
.
(1)若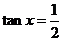 ,求
,求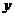 的值;
的值;
(2)若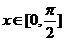 ,求函数单调区间及值域.
,求函数单调区间及值域.
10(13分)设函数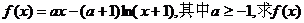 的单调区间.
的单调区间.
四、1答案:
7、概率:(Ⅰ)、“飞碟投入红袋”,“飞碟投入蓝袋”,“飞碟不入袋”分别记
为事件A,B,C. 则由题意知: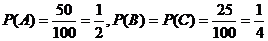
因每次投掷飞碟为相互独立事件,故4次投掷中恰有三次投入红袋的概率为;
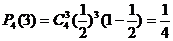
(Ⅱ)、两次投掷得分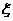 的得分可取值为0,1,2,3,4则:
的得分可取值为0,1,2,3,4则: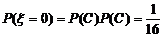
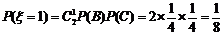
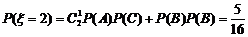
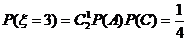 ;
;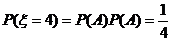
8、立体:(Ⅰ)由长方体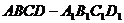 知:
知: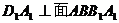 ,又
,又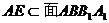 ,所以,
,所以,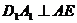 .
.
在矩形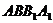 中,
中,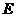 为
为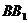 中点且
中点且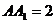 ,
,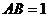 ,所以,
,所以,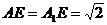 ,所以,
,所以,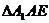 为等腰直角三角形,
为等腰直角三角形, .所以,
.所以,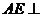 面
面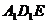 .所以,
.所以,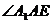 就是直线
就是直线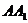 与平面
与平面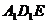 所成的角,为
所成的角,为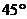 .
.
(Ⅱ) 注意到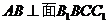 ,所以,面
,所以,面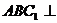
 ,所以,只需在
,所以,只需在 内过点
内过点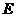 作
作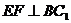 于F,则
于F,则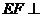 面
面 .
.
过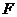 作
作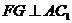 于G,连EG,则
于G,连EG,则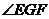 就是二面角
就是二面角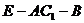 的平面角.
的平面角.
在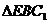 中,
中,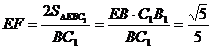 ,所以,
,所以,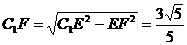 .
.
在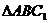 中,
中,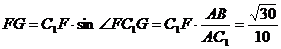 .
.
在 中,
中,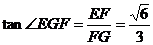 .
.
所以,二面角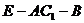 的平面角的大小为
的平面角的大小为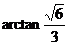 .
.
(Ⅲ)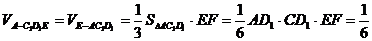 .
.
另一方面,也可以利用等积转化. 因为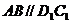 ,所以,
,所以,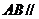
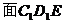 .所以,点A到平
.所以,点A到平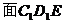 的距离就等于点
的距离就等于点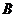 到平
到平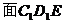 的距离.所以,
的距离.所以,
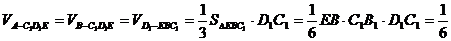 .12分
.12分
9、三角:解: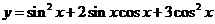
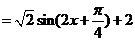
⑴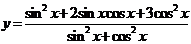
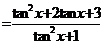
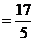 .
.
⑵在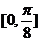 上单调递增,在
上单调递增,在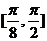 上单调递减.
上单调递减.
所以,当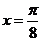 时,
时, ;当
;当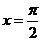 时,
时,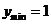 . 故
. 故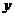 的值域为
的值域为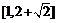 .
.
10、解:由已知得函数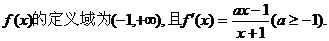
(1)当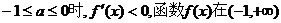 上单调递减。
上单调递减。
(2)当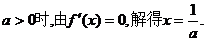
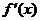 、
、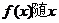 的变化情况如下表:
的变化情况如下表:
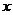
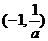
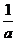
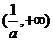
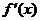
―
0
+
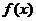

极小值

从上表可知
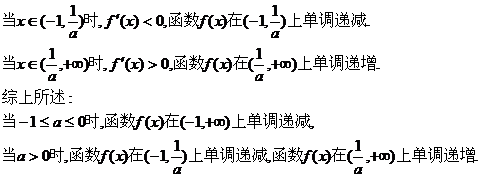
 2
2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com