
2009最有影响力高考复习题(数学)3(3+3+4)
文博浪花工作室王培博推荐(
一、选择题:
1、已知直线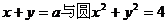 交于A、B两点,O是坐标原点,向量
交于A、B两点,O是坐标原点,向量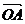 、
、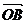 满足
满足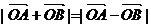 ,则实数a的值是( )答D
,则实数a的值是( )答D
A.2 B.-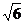 或-
或-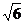 D.2或-2
D.2或-2
2、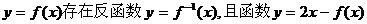 的图象过点(2,1),则函数
的图象过点(2,1),则函数 的图象一定过点( )答D
的图象一定过点( )答D
A.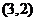 B.
B.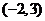 C.
C.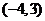 D.
D.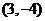
3、设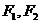 分别是双曲线
分别是双曲线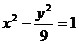 的左右焦点.若点P在双曲线上,且
的左右焦点.若点P在双曲线上,且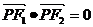 则
则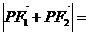 ( )答B
( )答B
A.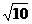 B.
B. 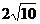 C.
C. 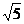 D.
D. 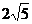
二、填空题:
4、在△ABC中,角A、B、C的对边分别为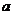 、
、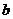 、
、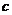 ,且
,且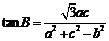 ,则角B的大小是 .
,则角B的大小是 .
 5、在
5、在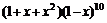 的展开式中,含
的展开式中,含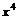 的系数为 .答135.
的系数为 .答135.
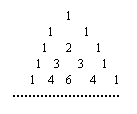
6、如右图,在杨辉三角形中,从上往下数共有n(n∈N*)行,在这些数中非1的数字之和为
答: 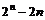
三、解答题:
7、某地的高考数学试卷中共有8道选择题,每个选择题都给了4个选项(其中有且仅有一个选项是正确的).评分标准规定:每题只选1项,答对得5分,不答或答错得0分.某考生每道题都给出了答案,已确定有4道题的答案是正确的,而其余的题中,有两道题每题都可判断其有两个选项是错误的,有一道题可以判断其一个选项是错误的,还有一道题因不理解题意只能乱猜.对于这8道选择题,试求:
(Ⅰ) 该考生得分为40分的概率;
(Ⅱ) 该考生所得分数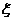 的分布列及数学期望
的分布列及数学期望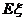 .
.
8、已知双曲线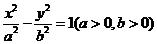 的离心率
的离心率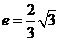 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为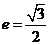 (1)求双曲线的方程;(2)直线
(1)求双曲线的方程;(2)直线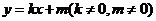 与该双曲线交于不同的两点
与该双曲线交于不同的两点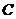 、
、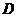 ,且
,且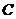 、
、 两点都在以A为圆心的同一圆上,求m的取值范围.
两点都在以A为圆心的同一圆上,求m的取值范围.
9、(14分)已知等差数列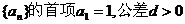 ,且第二项、第五项、第十 四项分别是一个等比数列的第二项、第三项、第四项.
,且第二项、第五项、第十 四项分别是一个等比数列的第二项、第三项、第四项.
(1)求数列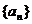 的通项公式;
的通项公式;
(2)设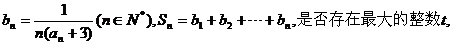 使得对任意的
使得对任意的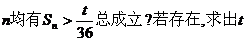 ;若不存在,请说明理由.
;若不存在,请说明理由.
(Ⅰ)求证: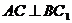 ;
;
(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)在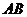 上是否存在点
上是否存在点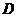 ,使得
,使得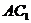 ∥平面
∥平面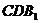 ,
,
若存在,试给出证明;若不存在,请说明理由
四、3答案:
4、由余弦定理,得 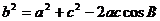 .则
.则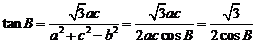 ,即
,即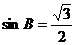 .所以B的大小是
.所以B的大小是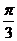 或
或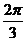 .
.
7、解: (Ⅰ)要得40分,8道选择题必须全做对,在其余四道题中,有两道题答对的概率为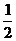 ,有一道题答对的概率为
,有一道题答对的概率为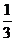 ,还有一道题答对的概率为
,还有一道题答对的概率为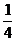 ,所以得40分的概率为
,所以得40分的概率为
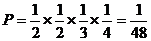 .
.
(Ⅱ)依题意,该考生得分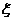 的取值是20,25,30,35,40,得分为20表示只做对了四道题,其余各题都做错,故所求概率为
的取值是20,25,30,35,40,得分为20表示只做对了四道题,其余各题都做错,故所求概率为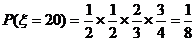 ;
;
同样可求得得分为25分的概率为
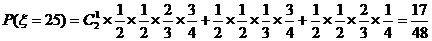 ;
;
得分为30分的概率为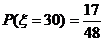 ;得分为35分的概率为
;得分为35分的概率为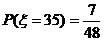 ;
;
得分为40分的概率为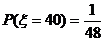 . 于是
. 于是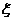 的分布列为
的分布列为
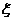
20
25
30
35
40
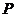
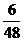
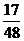
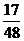
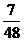
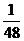
故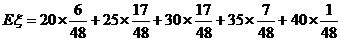 =
=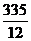 .所得分数的数学期望为
.所得分数的数学期望为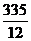 .
.
8、解析几何:(1) 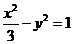 (2)
(2)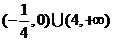
9、解:(I)由题意得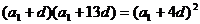 ,
,
整理得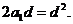
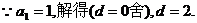
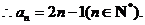
(II)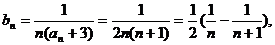
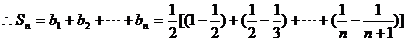
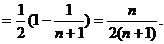 假设存在整数
假设存在整数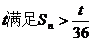 总成立。
总成立。
又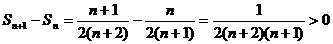 ,
,
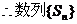 是单调递增的。
是单调递增的。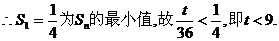
又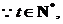
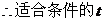 的最大值为8。
的最大值为8。
10、解法一: (Ⅰ)在直三棱柱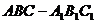 中,
中,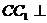 底面
底面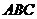 ,
,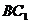 在底面上的射影为
在底面上的射影为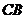 .
.
由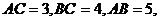 可得
可得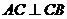 .,所以
.,所以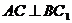 .
.
(Ⅱ)过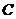 作
作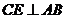 于
于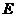 ,连结
,连结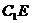 .
.
故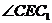 为二面角
为二面角 的平面角.
的平面角.
在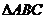 中,
中,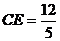 ,在Rt
,在Rt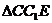 中,
中,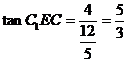 ,
,
故所求二面角的大小为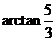 .
.
(Ⅲ)存在点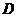 使
使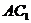 ∥平面
∥平面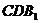 ,且
,且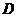 为
为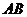 中点,下面给出证明.
中点,下面给出证明.
设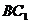 与
与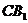 交于点
交于点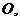 则
则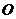 为
为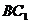 中点.在
中点.在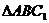 中, 连结
中, 连结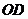 ,
,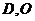 分别为
分别为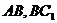 的中点,故
的中点,故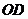 为
为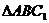 的中位线,
的中位线,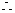
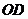 ∥
∥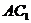 ,又
,又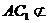 平面
平面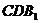 ,
,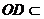 平面
平面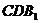 ,
,
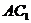 ∥平面
∥平面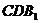 .故存在点
.故存在点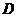 为
为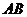 中点,使
中点,使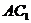 ∥平面
∥平面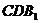 .
.
解法二
 直三棱柱
直三棱柱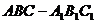 ,底面三边长
,底面三边长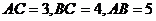 ,
,
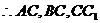 两两垂直.如图以
两两垂直.如图以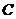 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系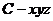 ,则
,则
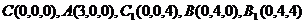 .
.
(Ⅰ)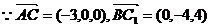 ,
,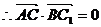 ,故
,故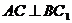 .
.
设平面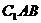 的一个法向量为
的一个法向量为 ,
,
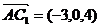 ,
,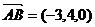 ,
,
由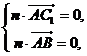 得
得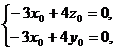
令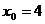 ,则
,则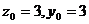 .则
.则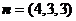 .
.
故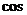 <
<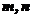 >=
>=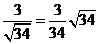 .所求二面角的大小为
.所求二面角的大小为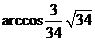 。 (Ⅲ)同解法一
。 (Ⅲ)同解法一
www.1010jiajiao.com
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com