
2009最有影响力高考复习题(数学)6(3+3+4)
文博浪花工作室王培博推荐(
一、选择题:
1、已知向量a= (cosθ,sinθ),向量b=(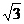 ,-1) , 则 |
,-1) , 则 |
A.4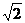 ,0
B.4,
,0
B.4,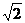
2、设f (x), g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f (x)g′(x)>0,且g(-3)=0, 则不等式f (x)g(x)<0的解集是 ( )
?A.(-3,0)∪(3,+∞) B.(-3,0)∪(0,3)
C.(-∞,-3)∪(3,+∞) D.(-∞,-3)∪(0,3)?
3、函数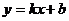 ,其中k,b
,其中k,b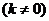 是常数,其图象是一条直线,称这个函数为线性函数,对于非线性可导函数
是常数,其图象是一条直线,称这个函数为线性函数,对于非线性可导函数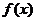 ,在点x0附近一点x的函数值
,在点x0附近一点x的函数值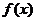 ,可以用如下方法求其近似代替值:
,可以用如下方法求其近似代替值: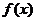
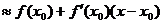 ,利用这一方法,
,利用这一方法,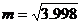 的近似代替值
的近似代替值
A.大于m B.小于m
C.等于m D.与m的大小关系无法确定
二、填空题:
4、已知命题P:.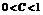 ,
,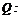 不等式
不等式 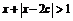 的解集为
的解集为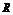 .如果
.如果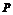 和
和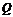 有且仅有一个正确,则
有且仅有一个正确,则 的取值范围是
.答
的取值范围是
.答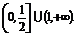
5、已知函数f (x)的定义域为(- ∞,2],部分对应值如下表. f ′ (x)为f (x)的导函数,函数y = f ′ (x)的图象如图所示. 若两正实数a,b满足|f (a+b)|<1,则 的取值范围是 .
6、一个与球心距离为2的平面截球所得的圆面面积为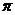 ,则球的表面积为
,则球的表面积为
三、解答题:
(I)求边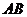 的长;
的长;
(II)若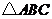 的面积为
的面积为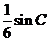 ,求角
,求角 的度数.
的度数.
8、已知:四棱锥P―ABCD,PA⊥平面ABCD,底面ABCD是直角梯形,∠A = 90°,且AB // CD,AB = CD,点F在线段PC上运动.
(1)当F为PC的中点时,求证:BF//平面PAD;
(2)设 = λ,求当λ为何值时有BF⊥CD.
9、在一次小测验中共有3道选择题和2道填空题,每答对一道题得20分,答错或不答得0分。某同学答对每道选择题的概率均为0.8,答对每道填空题的概率均为0.5,各道题答对与否互不影响.
(1)求该同学恰好答对2道选择题和1道填空题的概率;
(2)求该同学至多答对4道题的概率;
(3)若该同学已经答对了两道填空题,把这次测验的得分记为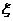 ,求
,求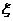 的概率分布列及数学期望
的概率分布列及数学期望
10、已知函数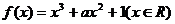
(1)若函数在点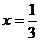 处取得极值,求实数a的值;
处取得极值,求实数a的值;
(2)求满足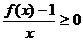 的x的集合
的x的集合
四、6答案
反向时有最大值4,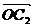 与
与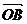 同向时有最小值0. ∴选D.?
同向时有最小值0. ∴选D.?
2、【解答】 设F(x)= f (x)g(x), 当x<0时,?∵F′(x)= f′(x)g(x)+f (x)g′(x)>0.?
∴F(x)在R上为增函数.?
∴F(x)在R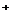 上亦为增函数.?
上亦为增函数.?
已知g(-3)=0,必有F(-3)=F(3)=0.?
构造如图的F(x)的图象,可知
F(x)<0的解集为x∈(-∞,-3)∪(0,3).?
3、【解答】A
4、【解答】若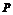 和
和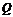 都正确,则由
都正确,则由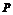 ,有
,有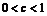 .由
.由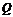 ,有
,有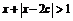 的解集为
的解集为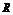 .
.
用函数认识不等式,只需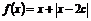 的最小值
的最小值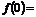 2
2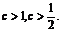 此时
此时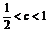 .
.
若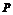 和
和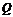 都不正确,则由
都不正确,则由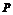 ,有
,有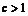 .由
.由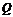 ,有
,有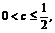 其交集为空集,此时
其交集为空集,此时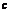 不存在.
不存在.
由题设知,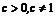 ,用补集思想,所求
,用补集思想,所求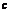 的取值范围为
的取值范围为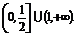
5、【解答】(- ∞,- 1)∪(1,+∞) 6、【解答】20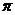
7、【解答】(I)由题意及正弦定理,得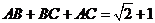 ,
,
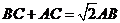 ,两式相减,得
,两式相减,得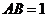 .
.
(II)由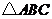 的面积
的面积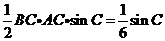 ,得
,得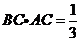 ,
,
由余弦定理,得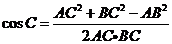
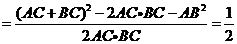 ,
,
所以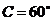 .
.
8、【解答】(1)取CD中点E,连结EF,BE. ∵F是PC中点,∴EF//PD.
∵EF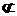 平面PAD,PD
平面PAD,PD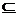 平面PAD,∴EF//平面PAD.
平面PAD,∴EF//平面PAD.
∵AB = CD,AB//CD,∴DEAB,∴BE//AD.
∵BE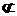 平面PAD,AD
平面PAD,AD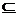 平面PAD,∴BE//平面PAD.
平面PAD,∴BE//平面PAD.
∵EF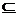 平面BEF,BE
平面BEF,BE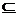 平面BEF,EF∩BE = E,∴平面BEF//平面PAD.
平面BEF,EF∩BE = E,∴平面BEF//平面PAD.
而BF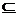 平面BEF,∴BF//平面PAD.
平面BEF,∴BF//平面PAD.
(2)当λ = 1,即F为PC中点时有BF⊥CD.
∵PA⊥平面ABCD,CD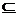 平面ABCD,∴PA⊥CD.
平面ABCD,∴PA⊥CD.
∵∠A = 90°,AB//CD,∴CD⊥AD.
∵PA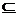 平面PAD,AD
平面PAD,AD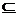 平面PAD,PA∩AD = A,
平面PAD,PA∩AD = A,
∴CD⊥平面PAD.
由(1)知平面PAD//平面BEF,∴CD⊥平面BEF.
∵BF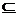 平面BEF,∴CD⊥BF.
平面BEF,∴CD⊥BF.
9、【解答】(1) 各道题答对与否互不影响,是独立事件:
. 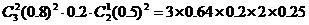 =0.192.
=0.192.
(2) “至多答对4道题”与“5道题全答对”是对立事件, 即
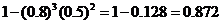
(3)
依题意: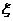 =40、60、80、100.
=40、60、80、100.
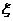
40
60
80
100
P
0.008
0.096
0.384
0.512
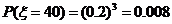 ;
;
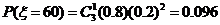
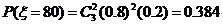 ;
; 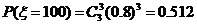
因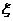 满足二项分布,故
满足二项分布,故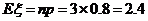
10、(1)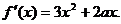
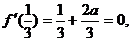
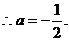
(2)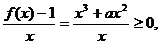
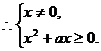
当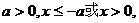 当
当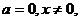 当
当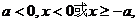
www.1010jiajiao.com
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com