
浙江省杭州学军中学2009届高三第十次月考
理科数学
一、选择题(每题5分,满分50分)
1.集合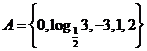 ,集合
,集合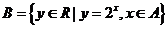 ,则
,则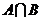 =( )
=( )
A.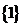 B.
B.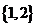 C.
C.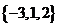 D.
D.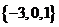
2. 设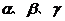 为平面,
为平面, 为直线,则
为直线,则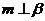 的一个充分条件为 ( )
的一个充分条件为 ( )
A.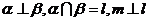 B.
B.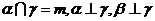
C.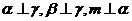 D.
D.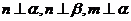
 3.将函数
3.将函数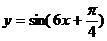 的图象上各点的横坐标伸长到原来的
的图象上各点的横坐标伸长到原来的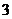 倍,再向右平移
倍,再向右平移 个单位,得到的函数的一个对称中心是
( )
个单位,得到的函数的一个对称中心是
( )
A. B.
B. C.
C.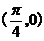 D.
D.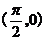
4.根据右边程序框图,若输出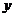 的值是4,则输入的实数
的值是4,则输入的实数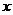 的
的
值为 ( )
(A) (B)
(B)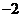 (C)
(C)  或
或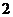 (D)
(D)  或
或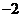
5.已知抛物线 的焦点为F,准线与x轴的交点为M,N为抛物线上的一点,且
的焦点为F,准线与x轴的交点为M,N为抛物线上的一点,且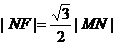 ,则
,则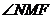 =( )
=( )
A. 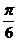 B.
B.
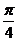 C.
C.
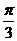 D.
D.
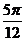
6.设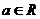 ,若函数
,若函数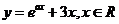 有大于零的极值点,则( )
有大于零的极值点,则( )
A.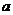 >-3
B.
>-3
B.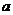 <
<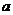 >
>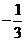 D.
D.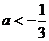
7.等差数列 的前n项和为
的前n项和为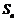 ,若
,若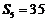 ,点A(3,
,点A(3,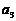 )与B(5,
)与B(5,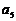 )都在斜率为-2的直线
)都在斜率为-2的直线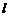 上,则直线
上,则直线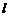 在第一象限内所有整点(横、纵坐标都是整数的点)的纵坐标的和为
(
)
在第一象限内所有整点(横、纵坐标都是整数的点)的纵坐标的和为
(
)
 A.16
B.
A.16
B.
8.已知如图,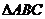 的外接圆的圆心为
的外接圆的圆心为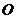 ,
, ,
,
则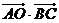 等于( )
等于( )
A.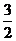 B.
B. C.
C.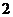 D.
D.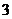
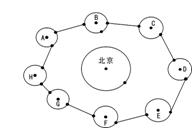 9.如图所示,北京城市的周边供外国人旅游的景点有8个,为了
9.如图所示,北京城市的周边供外国人旅游的景点有8个,为了
防止奥运期间景点过于拥挤,规定每个外国人一次只能游玩4个景
点,而且一次游玩景点中至多有两个相邻(如:选择A、B、E、F四
个景点也是允许的),那么外国人 现在要分两次把8个景点游
现在要分两次把8个景点游
玩好,不同的选择方法共有( )种.
A.60 B.42 C.30 D.14
10.定义在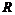 上的函数
上的函数 的图象关于点
的图象关于点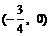 成中心对称,对任意实数
成中心对称,对任意实数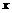 都有
都有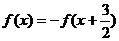 ,且
,且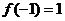 ,
, ,则
,则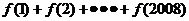 的值为
的值为
( )
A.-2 B.-1 C.0 D.1
二、填空题(每题4分,满分28分)
11.定义: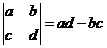 .若复数
.若复数 满足
满足 ,则
,则 等于
.
等于
.
12.若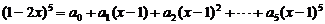 ,则
,则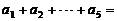 ____.
____.
(用数字作答)
13.已知函数 的
的
值范围为 .
14.在△ABC中,已知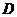 是
是 边上一点,若
边上一点,若 ,则
,则 的值为____ _ .
的值为____ _ .
15.已知圆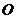 的方程为
的方程为 是圆
是圆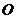 上的一个动点,若
上的一个动点,若 的垂直平分线总是被平面区域
的垂直平分线总是被平面区域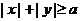 覆盖,则实数
覆盖,则实数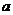 的取值范围是___ __.
的取值范围是___ __.
16.已知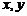 满足
满足 且目标函数
且目标函数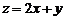 的最大值为7,最小值为1,
的最大值为7,最小值为1,
则 .
.
17.在棱长为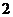 的正方体
的正方体 中,
中,
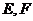 分别为棱
分别为棱 和
和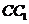 的中点,则线段
的中点,则线段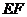 被正方体的内切球球面截在球内的线段长为_______________.
被正方体的内切球球面截在球内的线段长为_______________.
三、解答题(共72分)
18.在△ 中,角
中,角 所对边分别为
所对边分别为 ,且
,且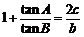 .
.
(Ⅰ)求角A;
(Ⅱ)若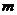
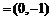 ,
,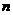
 ,试求|
,试求| |的最小值.
|的最小值.
19.已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球.现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为黑球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
(Ⅲ)设 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 的分布列和数学期望.
的分布列和数学期望.
(Ⅰ)求证: ;
;
(Ⅱ)试在棱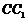 (不包含端点
(不包含端点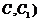 上确定一点
上确定一点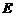 的位置,
的位置,
使得 (要求说明理由).
(要求说明理由).
(Ⅲ)在(Ⅱ)的条件下,若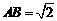 ,求二面角
,求二面角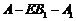 的平面角的正切值.
的平面角的正切值.
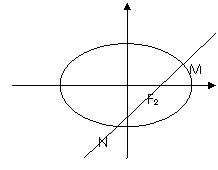 21.设椭圆
21.设椭圆 的一个顶点与抛物线
的一个顶点与抛物线 的焦点重合,
的焦点重合, ,
,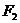 分别是椭圆的左、右焦点,离心率
分别是椭圆的左、右焦点,离心率 =,过椭圆右焦点
=,过椭圆右焦点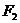 的直线
的直线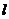 与椭圆
与椭圆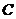 交于
交于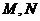 两点.
两点.
(Ⅰ)求椭圆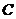 的方程;
的方程;
(Ⅱ)是否存在直线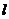 ,使得以线段
,使得以线段 为直径的圆过原点,若存在,求出直线
为直径的圆过原点,若存在,求出直线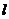 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(Ⅲ)若AB是椭圆C经过原点O的弦,MN∥AB,
求证:为定值.
22.已知函数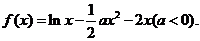
(Ⅰ)若函数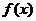 存在单调递减区间,求
存在单调递减区间,求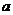 的取值范围;
的取值范围;
(Ⅱ)若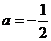 且关于x的方程
且关于x的方程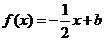 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;
(Ⅲ)设各项为正的数列 满足:
满足: 求证:
求证: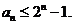
杭州学军中学高三理科数学第十次月考
数学参考评分标准(理科)
一. 选择题 : (本大题共10小题, 每小题5分, 共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
D
D
D
A
B
C
B
C
D
二.填空题: 本大题有 7小题, 每小题4分, 共28分. 把答案填在答题卷的相应位置上.
11. 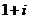 12.
-242
.
12.
-242
.
13 . ( )
14.
)
14.
 .
.
15. 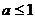 16.
-2
16.
-2
17. 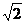 .
.
三. 解答题: 本大题有5小题, 共72分. 解答应写出文字说明, 证明过程或演算步骤.
18. (本小题满分14分)
答案:(1)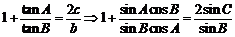 ,
,
即 ,
,
∴ ,∴
,∴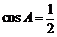 .
.
∵ ,∴
,∴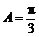 .(7分)
.(7分)
(2)m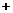 n
n  ,
,
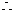 |m
|m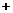 n|
n|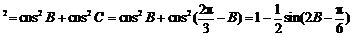 .
.
∵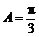 ,∴
,∴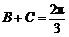 ,∴
,∴ .
.
从而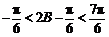 .
.
∴当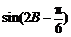 =1,即
=1,即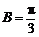 时,|m
时,|m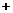 n|
n| 取得最小值
取得最小值 .
.
所以,|m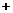 n|
n| .(7分)
.(7分)
19. (本小题满分14分)
(Ⅰ)解:设“从甲盒内取出的2个球均为黑球”为事件 ,“从乙盒内取出的2个球均为黑球”为事件
,“从乙盒内取出的2个球均为黑球”为事件 .由于事件
.由于事件 相互独立,且
相互独立,且 ,
,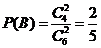 .
.
故取出的4个球均为黑球的概率为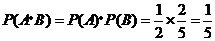 .(4分)
.(4分)
(Ⅱ)解:设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件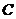 ,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件
,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件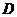 .由于事件
.由于事件 互斥,
互斥,
且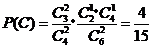 ,
,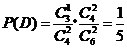 .
.
故取出的4个球中恰有1个红球的概率为 .(5分)
.(5分)
(Ⅲ)解: 可能的取值为
可能的取值为 .由(Ⅰ),(Ⅱ)得
.由(Ⅰ),(Ⅱ)得 ,
,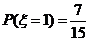 ,
,
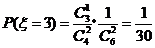 .从而
.从而 .
.
 的分布列为
的分布列为

0
1
2
3
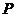

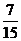


 的数学期望
的数学期望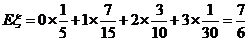 .(5分)
.(5分)
20.(本小题满分14分)
证(Ⅰ)因为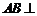 侧面
侧面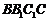 ,故
,故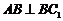
在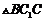 中,
中,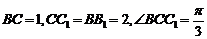 由余弦定理有
由余弦定理有
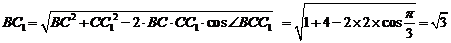
故有 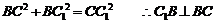
而  且
且 平面
平面
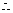
 ……………… 4分
……………… 4分
(Ⅱ)由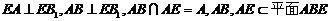
从而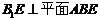 且
且 故
故
不妨设 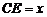 ,则
,则 ,则
,则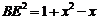
又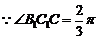 则
则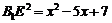
在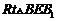 中有
中有
 从而
从而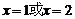 (舍去)
(舍去)
故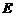 为
为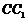 的中点时,
的中点时, ……………… 5分
……………… 5分
(Ⅲ)取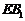 的中点
的中点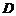 ,
, 的中点
的中点 ,
,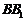 的中点
的中点 ,
, 的中点
的中点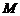
连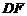 则
则 ,连
,连 则
则 ,连
,连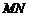 则
则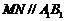
连 则
则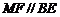 ,且
,且 为矩形,
为矩形,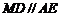
又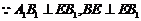 故
故 为所求二面角的平面角……………… 10分
为所求二面角的平面角……………… 10分
在 中,
中,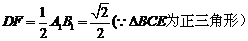

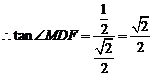 ……………… 5分
……………… 5分
21 . (本小题满分15分)
解:椭圆的顶点为(0,),即b=,
e==,所以a=2,2分
∴椭圆的标准方程为+=1 4分
(2) 不存在 .5分
(3)设M(x1,y1),N(x2,y2),A(x3,y3),B(x4,y4)
由(2)可得:|MN|=|x1-x2|=
==.
由消去y,并整理得x2=,
|AB|=|x3-x4|=4,11分
∴==4为定值. 5分
22.(本小题满分15分)
解:(1)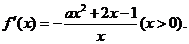 依题意
依题意 在
在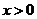 时有解:即
时有解:即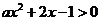 在
在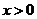 有解.则
有解.则 且方程
且方程 至少有一个正根.
至少有一个正根.
此时, …………………………………………………………4分
…………………………………………………………4分
(2)
设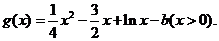 则
则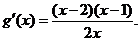 列表:
列表:
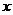
(0,1)
1
(1,2)
2
(2,4)
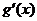
+
0

0
+
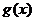
极大值
极小值
 -----6分
-----6分
 方程
方程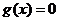 在[1,4]上恰有两个不相等的实数根.
在[1,4]上恰有两个不相等的实数根.
则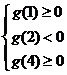 解得:
解得: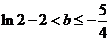 ……………………………………………5分
……………………………………………5分
(3)设 ,则
,则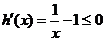
 在
在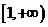 为减函数,且
为减函数,且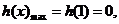 故当
故当 时有
时有 .
.
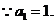 假设
假设 则
则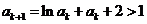 ,故
,故
从而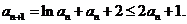
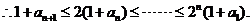
即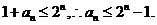 ……………………………………………5分
……………………………………………5分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com