|
试题详情
C. D. D.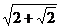 试题详情
试题详情
A. B. B.
 C. C.
 D. D.
 第Ⅱ卷(非选择题共90分) 本卷分必考题和选考题两部分。第13题~第21题为必考题,每个试题考生都必须做答。第22题~第24题为选考题,考生根据要求做答。 试题详情
二、填空题:本大题共4小题,每小题5分,共20分。 13.某地球仪上北纬30°纬线的长度为18 cm,则该地球仪的表面积是 cm2. cm,则该地球仪的表面积是 cm2. 试题详情
14.“渐升数”是指每个数字比它左边的数字大的正整数(如1458),若把四位“渐升数”按从小到大的顺序排列,则第30个数为 . 试题详情
试题详情
16.函数 上是减函数,则a的取值范围是 . 上是减函数,则a的取值范围是 . 试题详情
三、解答题:本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。
试题详情
 右图为中央电视台经济频道购物街栏目中的“幸运大转轮”.转轮被均匀分成20份,分别标有5~100的得分(得分都是5的倍数).每名游戏者至多可以选择转两次,两次得分相加之和若不超过100则为游戏者得分;若超过100则称“爆掉”,得0分. 右图为中央电视台经济频道购物街栏目中的“幸运大转轮”.转轮被均匀分成20份,分别标有5~100的得分(得分都是5的倍数).每名游戏者至多可以选择转两次,两次得分相加之和若不超过100则为游戏者得分;若超过100则称“爆掉”,得0分.
(Ⅰ) 若游戏者一定转两次,求出他“爆掉”的概率; 试题详情
(Ⅱ) 若一游戏者第一次转轮得分50,然后进行第二次转轮,写出他得分 的分布列,并求出得分的期望 的分布列,并求出得分的期望 ; ; 试题详情
 18.(本小题满分12分) 18.(本小题满分12分)
试题详情
试题详情
(Ⅰ)若输入 ,请写出由程序框图产生的数列 ,请写出由程序框图产生的数列 的所有项; 的所有项; (Ⅱ)若要程序框图产生一个无穷的常数列,试求出应输入的所有的初始数据x的值; 试题详情
(Ⅲ)输入初始数据x时,产生的无穷数列 满足:对任意正整数n,均有 满足:对任意正整数n,均有 ,求初始数据x的取值范围. ,求初始数据x的取值范围. 试题详情
19.(本小题满分12分) 下图是一几何体的直观图、主视图、俯视图、左视图. 试题详情
试题详情
(Ⅱ)证明: ∥面 ∥面 ; ; 试题详情
(Ⅲ)求面 与面 与面 所成的二面角(锐角)的余弦值. 所成的二面角(锐角)的余弦值. 试题详情
试题详情
试题详情
已知点 和点 和点 ,过点B的直线l和过点C的直线m相交于点A,且直线l和m的斜率之积为 ,过点B的直线l和过点C的直线m相交于点A,且直线l和m的斜率之积为 ,点A的轨迹(含点B、C)为曲线M. ,点A的轨迹(含点B、C)为曲线M. (Ⅰ)求曲线M的方程; (Ⅱ)曲线M的切线交x轴于点(a,0),求a的取值范围,及其切线方程. 试题详情
试题详情
试对实数 的不同取值,讨论关于x的方程 的不同取值,讨论关于x的方程 ,在 ,在 上的不同实数根的个数. 上的不同实数根的个数. 试题详情
请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分。做答时,用2B铅笔在答题卡上把所选题目对应的题号涂黑。 试题详情
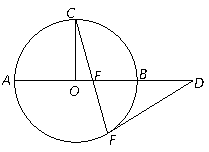 23.(本小题满分10分)选修4-1:几何证明选讲. 23.(本小题满分10分)选修4-1:几何证明选讲.
如图,AB是⊙O的直径,C,F是⊙O上的点,OC垂直于直径AB,过F点作⊙O的切线交AB的延长线于D.连结CF交AB于E点. 试题详情
(Ⅰ)求证: ; ; 试题详情
(Ⅱ)若⊙O的半径为 ,OB= ,OB= OE,求EF的长. OE,求EF的长. 试题详情
23.(本小题满分10分)选修4-4:坐标系与参数方程. 试题详情
(Ⅰ)已知点C极坐标为 ,求出以C为圆心,半径r=2的圆的极坐标方程(写出解题过程); ,求出以C为圆心,半径r=2的圆的极坐标方程(写出解题过程); 试题详情
试题详情
24.(本小题满分10分)选修4-5:不等式选讲. 试题详情
试题详情
(Ⅰ)求实数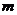 的取值范围: 的取值范围: 试题详情
(Ⅱ)在(Ⅰ)的条件下,当实数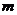 取得最大值时,试判断 取得最大值时,试判断 是否成立?并证明你的结论。 是否成立?并证明你的结论。 鞍山市2009年高三毕业班第一次质量调查考试 试题详情
一、选择题:每小题5分,满分60分. 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 D A A C D B A C C A D B 二、填空题:每小题4分,满分16分. 13.  14. 1359 15.  16. 三、解答题 17.解:(Ⅰ) 0.525 ……… 4分 (Ⅱ) 
0 55 60 65 70 75 80 85 90 95 100 P 










 ………12分 ………12分
18.解:(Ⅰ)由 ,得 ,得 , , ; ; 所以数列 只有三项: 只有三项: , , , , ……… 3分 ……… 3分 (Ⅱ)由题设 ,解得 ,解得 或 或 即当 或 或 时得到无穷的常数列 时得到无穷的常数列 或 或 ;……… 6分 ;……… 6分 (Ⅲ)解不等式 ,得 ,得 或 或 ……… 9分 ……… 9分 当 时, 时, , ,  ,与 ,与 矛盾; 矛盾; 当 时, 时, ,依此类推,可得 ,依此类推,可得 综上, ………12分 ………12分 19.解:(Ⅰ)由几何体的三视图可知,底面 是边长为 是边长为 的正方形, 的正方形, 面 面 , ,  ∥ ∥ , , . . 为 为 的中点 的中点 , , 又   面 面 ……… 4分 ……… 4分 (Ⅱ)取 的中点 的中点 , , 与 与 的交点为 的交点为 , , ∥ ∥ , ,  ∥ ∥ ,故BEMN为平行四边形 ,故BEMN为平行四边形  ∥ ∥  ∥面 ∥面 ……… 8分 ……… 8分 (Ⅲ)分别以 为 为 轴建立坐标系, 轴建立坐标系, 则 , , , ,  为 为 的中点, 的中点,
 面 面  为面 为面 的法向量, 的法向量, , , 设平面 的法向量为 的法向量为 , , 则  , , 与 与 的夹角为 的夹角为 ………11分 ………11分  面 面 与面 与面 所成的二面角(锐角)的余弦值为 所成的二面角(锐角)的余弦值为 ………12分 ………12分
20.解:(Ⅰ)设 ,由题设得 ,由题设得 ,整理得 ,整理得 其中 其中 , , 故点A的轨迹(含点B、C)M方程为 . ……… 4分 . ……… 4分 (Ⅱ)过点 ,与 ,与 轴平行的切线存在,此时 轴平行的切线存在,此时 , ……… 6分 , ……… 6分 设过点 ,斜率为 ,斜率为 的切线方程为 的切线方程为 ,于是 ,于是 整理得  此方程有重根 此方程有重根  即 即
即 解得 解得 且 且 ………10分 ………10分 所求切线方程为
 ………12分 ………12分 21.解:由 ,得 ,得 , , 于是 ……… 3分 ……… 3分 考察函数 ,可知 ,可知 ……… 6分 ……… 6分 在 上, 上,  和 和 变化情况如下表: 变化情况如下表: x 0 









0 - - 0 + + 0 - 0 + 
0 ↓ ↓ 1 ↑ ↑ 0 ↓ 
↑ ……… 9分 从而,可得圆方程不同实数根的个数如下: 当 或 或 或 或 时,有2个;当 时,有2个;当 时,有3个; 时,有3个; 当 时,有4个;当 时,有4个;当 时,有0个; 时,有0个; 当 时,有1个. ………12分 时,有1个. ………12分 22解:(Ⅰ)连结OF.∵DF切⊙O于F,∴∠OFD=90°.∴∠OFC+∠CFD=90°. ∵OC=OF,∴∠OCF=∠OFC.∵CO⊥AB于O,∴∠OCF+∠CEO=90°. ∴∠CFD=∠CEO=∠DEF,∴DF=DE. ∵DF是⊙O的切线,∴DF2=DB?DA.∴DE2=DB?DA. ……… 5分 (Ⅱ) ,CO= ,CO= , ,  . . ∵CE?EF= AE?EB= ( +2)( +2)( -2)=8,∴EF=2. ………10分 -2)=8,∴EF=2. ………10分 23解:(Ⅰ)设M为圆上一点,坐标为 ,则∠ ,则∠ 或 或 , , 由余弦定理得 ∴极坐标方程为 ∴极坐标方程为 ……… 5分 ……… 5分 (Ⅱ) 的普通方程为 的普通方程为 ,圆心 ,圆心 ,半径 ,半径 . .  的普通方程为 的普通方程为 . .
因为圆心 到直线 到直线 的距离为 的距离为 , , 所以 与 与 只有一个公共点. ………10分 只有一个公共点. ………10分 24.解:(Ⅰ)由绝对值不等式性质知:  对 对 恒成立 恒成立
故 的解集为 的解集为 ,只须 ,只须 既可 既可   的取值范围是 的取值范围是 ……… 5分 ……… 5分
(Ⅱ)由(Ⅰ)知实数 的最大值为3,当 的最大值为3,当 时, 时, 成立 成立 证明如下:(利用分析法)要使 成立 成立 只须 等价于 等价于  等价于  等价于 等价于 ,而 ,而 显然成立, 显然成立, 以上每一步均可逆推,故所证明不等式成立。 ………10
| 

 (
( 是虚数单位)相等的是
是虚数单位)相等的是 B.
B. C.
C. D.
D.
 ,设
,设 ,则集合
,则集合 的真子集个数为
的真子集个数为 B.
B. C.
C.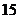 D.
D.
 的图像,只需要将
的图像,只需要将 的图象
的图象 个单位 B.向右平移
个单位 B.向右平移 个单位
个单位 个单位 D.向左平移
个单位 D.向左平移 个单位
个单位 ,那么△ABC一定是
,那么△ABC一定是 表示的平面区域面积是9,则
表示的平面区域面积是9,则
 B.―
B.― C.―5 D.1
C.―5 D.1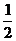 C.3 D.
C.3 D.
 则
则 的最小值是
的最小值是

 上的一点
上的一点 作圆
作圆 的两条切线
的两条切线 为切点,当直线
为切点,当直线 关于直线
关于直线 对称时,则
对称时,则
 10.如图所示,墙上挂有一边长为a的正方形木板,上面画有抛物线型的图案(阴影部分),某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是
10.如图所示,墙上挂有一边长为a的正方形木板,上面画有抛物线型的图案(阴影部分),某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是 A.
A. B.
B. C.
C. D.与a的取值有关
D.与a的取值有关