
广东省珠海市2009年高三第二次调研考试
数学(文科)试题
一.选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.函数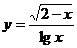 的定义域是
的定义域是
A.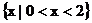 B.
B.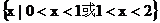
C.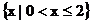 D.
D.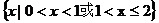
2.若复数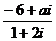 是纯虚数(i是虚数单位),则实数a的值为
是纯虚数(i是虚数单位),则实数a的值为
A.6 B.-6 C.3 D.-3
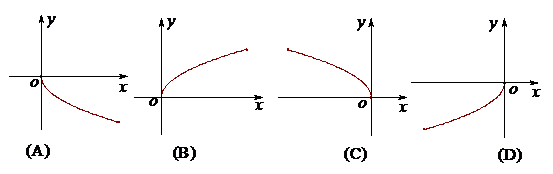
3.函数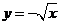 的大致形状是
的大致形状是
4.已知等差数列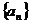 中,
中,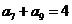 则数列
则数列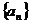 的前15项和是
的前15项和是
A.28 B.30 C.32 D.35
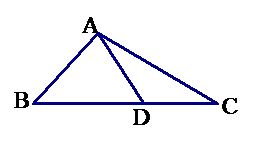 5.如图,在
5.如图,在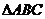 中,已知
中,已知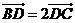 ,则
,则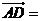
A.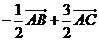 B.
B.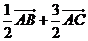
C.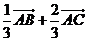 D.
D.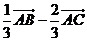
6.如果实数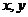 满足:
满足: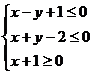 ,则目标函数
,则目标函数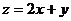 的最大值为
的最大值为
A.2 B.3 C.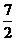 D.4
D.4
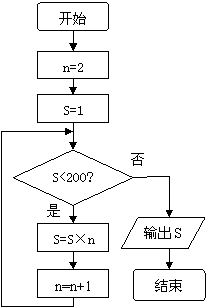 7.右边流程图中, 语句“
7.右边流程图中, 语句“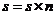 ”将被执行的次数是
”将被执行的次数是
A.4 B.5
C.6 D.7
8.将函数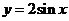 图象上的所有点的横坐标缩小到原来的
图象上的所有点的横坐标缩小到原来的 (纵坐标不变),得到图象
(纵坐标不变),得到图象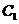 ,再将图象
,再将图象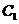 沿
沿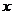 轴向左平移
轴向左平移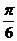 个单位,得到图象
个单位,得到图象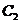 ,则图象
,则图象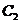 的解析式可以是B
的解析式可以是B
A.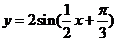 B.
B.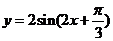
C. 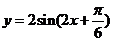 D.
D.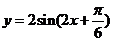
9.点P在圆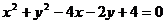 上,则点P到直线
上,则点P到直线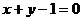 的最短距离是
的最短距离是
A.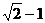 B.
B.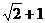 C.
C.
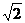 D.0
D.0
10.下列四种说法中,错误的个数是
①.命题“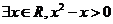 ”的否定是“
”的否定是“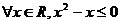 ” ;
” ;
②.“命题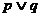 为真”是“命题
为真”是“命题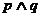 为真”的必要不充分条件;
为真”的必要不充分条件;
③.“若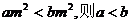 ”的逆命题为真;
”的逆命题为真;
④.若实数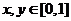 ,则满足:
,则满足: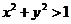 的概率为
的概率为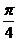 .
.
A.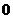 B.1
C.2 D.3
B.1
C.2 D.3
二.填空题:本大题共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.
11.以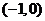 为顶点且离心率为
为顶点且离心率为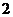 的双曲线的标准方程是
的双曲线的标准方程是
12.宏景居民小区由A.B.C.D四个片组成,其中A片有340人,B片有620人,C片有460人,D片有500人.现准备对居民进行问卷调查,采用分层抽样的方法,从四个片区中随机抽取若干名进行调查.现知从A片抽取的人数为17人,则从C片抽取的人数应为____________.
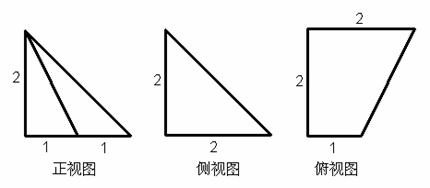
13.一个五面体的三视图如下,正视图与侧视图是等腰直角三角形,俯视图为直角梯形,部分边长如图所示,则此五面体的体积为
14.(几何证明选讲选做题)
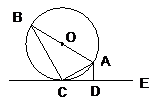 如下图,AB是圆O的直径,直线CE和圆O相切于点C,
如下图,AB是圆O的直径,直线CE和圆O相切于点C,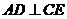 于D,若AD=1,
于D,若AD=1,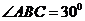 ,则圆O的面积是
.
,则圆O的面积是
.
15.(坐标系与参数方程选做题)
在极坐标系中,点A和点B的极坐标分别为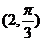 和
和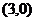 ,O为极点,则三角形OAB的面积=_____.
,O为极点,则三角形OAB的面积=_____.
三.解答题:本大题共6小题,满分80分.解答须写出文字说明.证明过程和演算步骤.
16.(本小题满分12分)
已知直角坐标平面上四点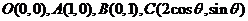 ,满足
,满足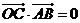 .
.
(1)求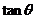 的值;(2)求
的值;(2)求 的值.
的值.
17.(本小题满分12分)
一个袋子中有蓝色球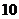 个,红.白两种颜色的球若干个,这些球除颜色外其余完全相同.
个,红.白两种颜色的球若干个,这些球除颜色外其余完全相同.
(1)甲从袋子中随机取出1个球,取到红球的概率是
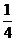 ,放回后乙取出一个球,取到白球的概率是
,放回后乙取出一个球,取到白球的概率是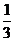 ,求红球的个数;
,求红球的个数;
(2)从袋子中取出4个红球,分别编号为1号.2号.3号.4号.将这四个球装入一个盒子中,甲和乙从盒子中各取一个球(甲先取,取出的球不放回),求两球的编号之和不大于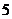 的概率.
的概率.

18.(本小题满分14分)
(立体几何题目选)如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,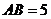
AA1=4,点D是AB的中点.
(1)求证:AC⊥BC1;
(2)求证:AC 1//平面CDB1;
(3)求多面体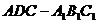 的体积.
的体积.
19.(本小题满分14分)
已知椭圆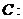
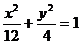 ,
,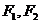 是其左右焦点.
是其左右焦点.
(1)若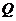 为椭圆上动点,求
为椭圆上动点,求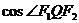 的最小值;
的最小值;
(2)若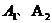 分别是椭圆长轴的左右端点,
分别是椭圆长轴的左右端点,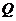 为椭圆上动点,设直线
为椭圆上动点,设直线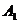
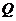 斜率为
斜率为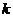 ,且
,且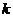
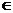
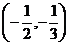 ,求直线
,求直线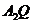 斜率的取值范围.
斜率的取值范围.
20.(本小题满分14分)
已知正数数列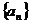 满足:
满足: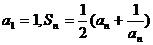 ,其中
,其中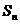 为数列
为数列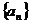 的前
的前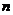 项和.
项和.
(1)求数列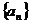 的通项
的通项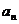 ;
;
(2)求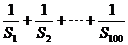 的整数部分.
的整数部分.
21.(本小题满分14分)
设函数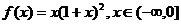 ,
,
(1)求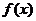 的极值点;
的极值点;
(2)对任意的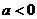 ,以
,以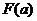 记
记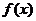 在
在 上的最小值,求
上的最小值,求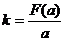 的最小值.
的最小值.
DCABC CBBAC
11
12 23
13 2
14 4π
15

16解 (1)




 1分
1分





 2分
2分
由已知有



 4分
4分





 6分
6分
(2)



 10分
10分
= 




 11分
11分
= 



 12分
12分
17解:(1)设红球有 个,白球
个,白球 个,依题意得
个,依题意得 



 1分
1分
 ,
,




 3分
3分
解得
故红球有6个.




 5分
5分
(2)记“甲取出的球的编号大”为事件A,
所有的基本事件有:(1,2),(l,3),(1,4),
(2,1),(2,3),(2,4),
(3,1),(3,2),(3,4),
(4,1),(4,2),(4,3),
共12个基本事件 



 8分
8分
事件A包含的基本事件有:(1,2),(1,3),(1,4)(2,1),
(2,3),(3,1),(3,2)(4,1),
共8个基本事件




 11分
11分
所以,. 




 12分
12分
18解:(1)底面三边长AC=3,BC=4,AB=5,
∠ACB=90°,∴ AC⊥BC, (2分)
又在直三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC 底面ABC,∴CC1⊥AC,(3分)
底面ABC,∴CC1⊥AC,(3分)
BC.CC1 平面BCC1,且BC 与CC1相交
平面BCC1,且BC 与CC1相交
∴ AC⊥平面BCC1; (5分)
而BC1 平面BCC1
平面BCC1
∴ AC⊥BC1 (6分)
(2)设CB1与C1B的交点为E,连结DE,∵ D是AB的中点,E是BC1的中点,
∴ DE//AC1, (8分)
∵ DE 平面CDB1,AC1
平面CDB1,AC1 平面CDB1,
平面CDB1,
∴ AC1//平面CDB1;(10分)
(3) (11分)
(11分)
= -
- (13分)
(13分)
=20 (14分)
19解:(1)设椭圆的半长轴长.半短轴长.半焦距分别为a,b,c,则有
 ,
,
由椭圆定义,有 ………1分
………1分
 =
= ……………………………2分
……………………………2分
= ……………………3分
……………………3分
≥ …………………………………………5分
…………………………………………5分
= =
= ……………………………………………6分
……………………………………………6分
∴ 的最小值为
的最小值为 。
。
(当且仅当 时,即
时,即 取椭圆上下顶点时,
取椭圆上下顶点时, 取得最小值 )………………………………………7分
取得最小值 )………………………………………7分
(2)设 的斜率为
的斜率为 ,
,
则 ,
…………………………………………8分
,
…………………………………………8分
 …………………………………………9分
…………………………………………9分
∴ =
= 及
及 …………………………………………10分
…………………………………………10分
则 =
= =
= 又
又 …………………………………………12分
…………………………………………12分
∴ …………………………………………13分
…………………………………………13分
故 斜率的取值范围为(
斜率的取值范围为( ) …………………………………………14分
) …………………………………………14分
20解:(1)

 ,……………………1分
,……………………1分
即 ,
,
即 ,
, ,
…………………………………………2分
,
…………………………………………2分
∴ 为等差数列,
…………………………………………3分
为等差数列,
…………………………………………3分
又 ,
…………………………………………4分
,
…………………………………………4分
∴ ,
…………………………………………5分
,
…………………………………………5分
∴ …………………………………………7分
…………………………………………7分
(2) …………………………………………8分
…………………………………………8分
当 时,
时,

…………………………………………11分

 ,
,
…………………………………………13分
 的整数部分为18。
…………………………………………14分
的整数部分为18。
…………………………………………14分
21解:(1) ………(1分)
………(1分)
由 解得:
解得: ………(2分)
………(2分)
当 或
或 时,
时, ………(3分)
………(3分)
当 时,
时, ………(4分)
………(4分)
所以,有两个极值点:
 是极大值点,
是极大值点, ;
………(5分)
;
………(5分)
 是极小值点,
是极小值点, 。 ………(6分)
。 ………(6分)
(2) 过点 做直线
做直线 ,与
,与 的图象的另一个交点为A
的图象的另一个交点为A ,则
,则 ,即
,即 ………(8分)
………(8分)
已知有解 ,则
,则

解得 ………(10分)
………(10分)
当 时,
时, ;
; ………(11分)
………(11分)
当 时,
时, ,
, ,
,
其中当 时,
时, ;………(12分)
;………(12分)
当 时,
时, ……(13分)
……(13分)
所以,对任意的 ,
, 的最小值为
的最小值为 (其中当
(其中当 时,
时, ).……(14分)
).……(14分)
(以上答案和评分标准仅供参考,其它答案,请参照给分)lf
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com