
题目列表(包括答案和解析)
| π |
| 4 |
| fn(θ) | fn(θ)的 单调性 |
fn(θ)的最小值及取得最小值时θ的取值 | fn(θ)的最大值及取得最大值时θ的取值 |
| n=1 | |||
| n=2 | |||
| n=3 | |||
| n=4 | |||
| n=5 | |||
| n=6 |
心脏每跳动一次,就完成一次收缩和舒张.心脏跳动时,血压在增大或减小,并呈周期性变化.血压的最大值、最小值分别称为收缩压和舒张压,血压计上的读数就是收缩压和舒张压.健康成年人的收缩压和舒张压一般为120~140![]() 和60~90
和60~90![]() . 设某成年人的血压满足函数式
. 设某成年人的血压满足函数式![]() ,其中
,其中![]() 为血压
为血压![]() ,
,![]() 为时间
为时间![]() ,
,![]() .试回答下列问题:
.试回答下列问题:
(Ⅰ)求函数![]() 的周期;
的周期;
(Ⅱ)求此人每分钟心跳的次数;
(Ⅲ)求出此人的血压在血压计上的读数,并说明此人的血压是否正常.
(Ⅳ)在某些时间段内,此人的血压是持续升高的.试写出所有这样的时间段.
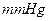 和60~90
和60~90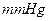 . 设某成年人的血压满足函数式
. 设某成年人的血压满足函数式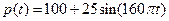 ,其中
,其中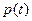 为血压
为血压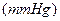 ,
,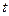 为时间
为时间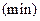 ,
,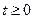 .试回答下列问题:
.试回答下列问题: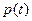 的周期;
的周期;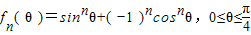 ,其中n为正整数.
,其中n为正整数.| fn(θ) | fn(θ)的 单调性 | fn(θ)的最小值及取得最小值时θ的取值 | fn(θ)的最大值及取得最大值时θ的取值 |
| n=1 | |||
| n=2 | |||
| n=3 | |||
| n=4 | |||
| n=5 | |||
| n=6 |
我们用min{S1,S2,…,Sn}和max{S1,S2,…,Sn}分别表示实数S1,S2,…,Sn中的最小者和最大者.
(1)设f(x)=min{sinx,cosx},g(x)=max{sinx,cosx},x∈[0,2π],函数f(x)的值域为A,函数g(x)的值域为B,求A∩B;
(2)数学课上老师提出了下面的问题:设a1,a2,an为实数,x∈R,求函数![]() (x1<x2<xn∈R=的最小值或最大值.为了方便探究,遵循从特殊到一般的原则,老师让学生先解决两个特例:求函数
(x1<x2<xn∈R=的最小值或最大值.为了方便探究,遵循从特殊到一般的原则,老师让学生先解决两个特例:求函数![]() 和
和![]() 的最值.学生甲得出的结论是:[f(x)]min=min{f(-2),f(-1),f(1)},且f(x)无最大值.学生乙得出的结论是:[g(x)]max=max{g(-1),g(1),g(2)},且g(x)无最小值.请选择两个学生得出的结论中的一个,说明其成立的理由;
的最值.学生甲得出的结论是:[f(x)]min=min{f(-2),f(-1),f(1)},且f(x)无最大值.学生乙得出的结论是:[g(x)]max=max{g(-1),g(1),g(2)},且g(x)无最小值.请选择两个学生得出的结论中的一个,说明其成立的理由;
(3)试对老师提出的问题进行研究,写出你所得到的结论并加以证明(如果结论是分类的,请选择一种情况加以证明).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com