
题目列表(包括答案和解析)
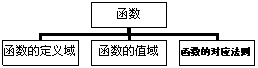
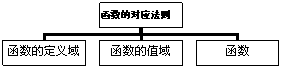
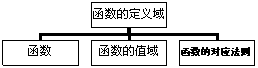
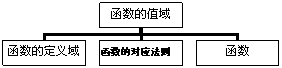
4.下列关于函数、函数的定义域、函数的值域、函数的对应法则的结构图正确的是( )

2.两个变量y与x的回归模型中,分别选择了4个不同的模型,它们的相关指数R2如下,其中拟和效果最好的模型是( )
A.模型1的相关指数R2为0.25 B.模型2的相关指数R2为0.80
C.模型3的相关指数R2为0.50 D.模型4的相关指数R2为0.98
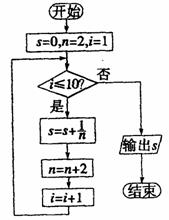 3.如图所示的程序框图所进行的求和运算是( )
3.如图所示的程序框图所进行的求和运算是( )
A.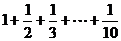
B.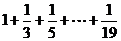
C.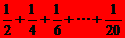
D.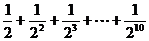
1.双曲线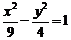 的渐近线方程是
( )
的渐近线方程是
( )
A.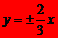 B.
B.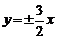 C.
C.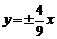 D.
D.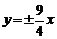
22.(本小题满分10分)
已知函数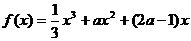 .
.
(1)若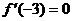 ,求
,求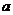 的值;
的值;
(2)若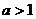 ,求函数
,求函数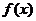 的单调区间与极值点;
的单调区间与极值点;
(3)设函数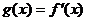 是偶函数,若过点
是偶函数,若过点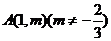 可作曲线
可作曲线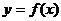 的三条切线,求实数
的三条切线,求实数 的取值范围.
的取值范围.
福建省霞浦一中09-10学年高二上学期期末测试
21.(本小题满分10分)
设椭圆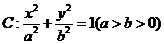 过点
过点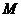 (
(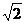 ,1),且左焦点为
,1),且左焦点为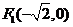 .
.
(1)求椭圆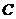 的方程;
的方程;
(2)判断是否存在经过定点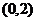 的直线
的直线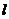 与椭圆
与椭圆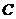 交于
交于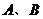 两点并且满足
两点并且满足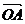 ·
·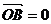 ,
,
若存在求出直线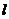 的方程,不存在说明理由。
的方程,不存在说明理由。
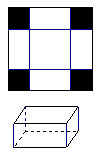
20.(本小题满分8分)
如图一边长为30cm的正方形铁皮,四角各截去一个大小相同的小正方形,然后折起来做成一个无盖的长方体盒子,小盒子的容积V(单位: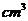 )是关于截去的小正方形的边长
)是关于截去的小正方形的边长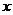 (单位:cm)的函数.写出V关于
(单位:cm)的函数.写出V关于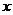 的函数式,
的函数式,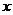 为多少时小盒子的容积最大?最大容积是多少?
为多少时小盒子的容积最大?最大容积是多少?
19.(本小题满分8分)
在平面直角坐标系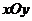 中,抛物线
中,抛物线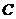 的顶点是坐标原点且经过点
的顶点是坐标原点且经过点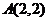 ,其焦点
,其焦点 在
在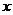 轴上。
轴上。
(1)求抛物线方程;(2)求过点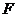 且与直线
且与直线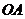 垂直的直线方程。
垂直的直线方程。
18.(本小题满分8分)
将一颗骰子先后抛掷2次,观察向上的点数,求:
(1)两数之和为6的概率;
(2)向上的点数不同的概率;
(3)以第一次向上点数为横坐标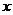 ,第二次向上的点数为纵坐标
,第二次向上的点数为纵坐标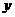 的点(
的点(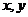 )在圆
)在圆
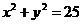 的内部的概率。
的内部的概率。
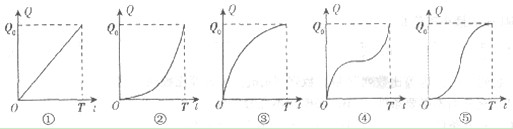
17.家电下乡政策是应对金融危机、积极扩大内需的重要举措.我省某家电制造集团为尽快实现
家电下乡提出五种运输方案,据预测,这五种方案均能在规定时间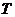 内完成预期的运输任务Q0,
内完成预期的运输任务Q0,
各种方案的运输总量Q与时间t 的函数关系如下图所示.在这五种方案中,运输效率(单位时间的
运输量)逐步提高的是_________.(填写所有正确的图象的编号)
16.过抛物线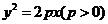 的焦点F作倾斜角为
的焦点F作倾斜角为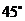 的直线交抛物线于A、B两点,若线段AB的长为8,则
的直线交抛物线于A、B两点,若线段AB的长为8,则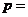 _____.
_____.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com