a)　　 写出所有符合条件的排列和组合:

例1：有甲、乙、丙、丁四队进行篮球单循环赛：

　　　　　　　　　　　　 i.　　　　　　　 写出所有冠、亚军的可能性.

　　　　　　　　　　　 ii.　　　　　　　 写出各场比赛的双方.

b)　　 含有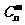或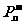的方程、不等式的证明或求解:

例2：(1)求证：.

(2)已知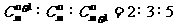：，求m、n.

c)　　 排列组合应用题：

例3：已知A={1，2，3，4，5，6}，问

(1)集合A有　　　　　　　　　　 个子集.

(2)集合A可以组成多少个含有元素2的子集。

(3)集合A中的六个数字可组成多少个含有两个以上的不同数字的数？

例4：从-2，-1，0，1，2，3，4这七个数字中任选3个不同数字分别作为a、b、

c的值，可组成多少个顶点在y轴左侧的二次函数f(x)=ax²+bx+c解解析式.

3.(选做)小李打算从10位朋友中邀请4位去旅游，这10位朋友中，有一对双胞胎，对这两位朋友，要么邀请，要么不邀请.求不同的邀请方案的种数.

2.书架上竖排着六本数，现将新购的3本书上架，要求不调乱书架上原有的书，那么不同的上架方式共有多少种？

1.①8人站成一排，不同的站法有　　　　　 种.

(A)10080　　 (B)13440　　 (C)20160　　 (D)40320.

②6人站成一排，甲不站头，乙不站尾，不同的站法有　　　　 种.

(A)504　　　 (B)480　　　 (C)360　　　 (D)240.

③5件不同礼品分送给4人，每人至少一件，而且礼品全部送出，那么送出礼品的方法数是　　　　　 .

(A)960　　 (B)480　　 (C)240　　　 (D)120.

④4个小组，分别从3个风景点中选一处进行观光旅游，不同的选择方案的种数是　　　　 .

(A)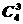　　　 (B)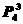　　　 (C)3⁴　　　 (D)4³

4. 含有条件的排列组合应用题：

例1：某班有男生25人，女生21人，现选男生3人，女生2人分别担任正、副班长、学委、体委、宣委，问有多少种不同的选举方法？

上题中，(1)如果由25名男生中选3人担任班长、学委、体委，女生中选2人担任副班长、宣委，问有多少种不同的选法？

(2)若25名男生中选3人，21名女生中选2人，分别担任正、副班长、学委、体委、宣委，若正班长必须由男生担任，问有多少种不同的选法？

例2：从1到9这9个数字中取5个数字排列，奇数只能排在个位、十位或百位，问这样的无重复的五位数有多少个？

例3： 4人分住两个房间，每个房间至少住进1人，求不同的安排方法数？

例4：圆周上有8个点，将圆周等分，那么以其中的3个点为顶点的直角三角形共有　　　　 个.

(A)12　　　 (B)16　　　 (C)24　　　 (D)48

课后练习与检测：

13、先后抛掷一枚骰子两次，将得到的点数分别记为，。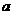

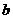(1)求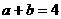的概率；

(2)求点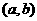在函数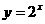图像上的概率；

(3)将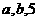的值分别作为三条线段的长，求这三条线段能围成等腰三角形的概率。

12、如图，在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形，现有均匀的粒子散落在正方形中，问粒子落在中间带形区域的概率是多少？

11、甲盒中有一个红色球，两个白色球，这3个球除颜色外完全相同，有放回地连续抽取2个，每次从中任意地取出1个球，用列表的方法列出所有可能结果，计算下列事件的概率。

(1)取出的2个球都是白球； (2)取出的2个球中至少有1个白球。

10、某小组有三名女生，两名男生，现从这个小组中任意选出一名组长，则其中一名女生小丽当选为组长的概率是___________。