37、如图所示，MN、PQ是相互交叉成60°角的光滑金属导轨，O是它们的交点且接触良好．两导轨处在同一水平面内，并置于有理想边界的匀强磁场中(图中经过O点的虚线即为磁场的左边界)．导体棒ab与导轨始终保持良好接触，并在弹簧S的作用下沿导轨以速度v₀向左匀速运动．已知在导体棒运动的过程中，弹簧始终处于弹性限度内．磁感应强度的大小为B，方向如图．当导体棒运动到O点时，弹簧恰好处于原长，导轨和导体棒单位长度的电阻均为r，导体棒ab的质量为m．求：

(1)导体棒ab第一次经过O点前，通过它的电流大小；

(2)弹簧的劲度系数k；

(3)从导体棒第一次经过O点开始直到它静止的过程中，导体棒ab中产生的热量．

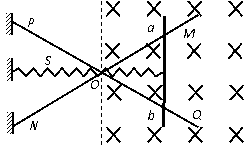
解：(1)设ab棒在导轨之间的长度为l，由欧姆定律得

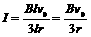　　　　　　　　　　　　　　　　　　　　　 (3分)

(2)设O点到ab棒距离为x，则ab棒的有效长度l' =2xtan30°=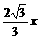　 (2分)

∵ab棒做匀速运动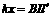，∴　　　　　　　　　　　　　　　　　　　 (2分)

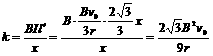∴ 　　　　　　　　　　　　　　　　　(1分)

(3)裸导线最终只能静止于O点，故其动能全部转化为焦耳热，即

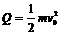　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (2分)

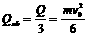则　　　　　　　　　　 　　　　　　　　　　　　　　　　(2分)

36、如图所示，导体棒ab、cd放在光滑水平导轨上，cd棒通过滑轮悬挂一质量为m的物块，整个装置处于磁感应强度大小为B、方向竖直向下的匀强磁场中．ab在外力作用下以速度v₁匀速向右运动时，cd棒由静止释放，设ab、cd的长度均为L，ab棒的电阻为r₁，cd棒的电阻为r₂，导轨足够长且电阻不计，求：

(1)cd棒开始运动的方向与ab棒匀速运动速度v₁取值的关系；

(2)稳定状态时，cd棒匀速运动的速度；

(3)稳定状态时，回路的电功率P_电和外力的功率P_外．

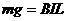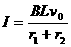(1)cd棒静止　 (1分) 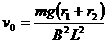　(1分) (1分)　

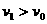　 ，cd棒开始向右运动； (1分)　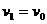 ，cd棒静止； (1分)

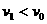，cd棒开始向左运动　 (1分)

(2)cd棒匀速运动可能有两种情况：匀速向右运动和匀速向左运动

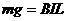
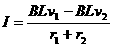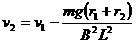cd棒匀速向右运动时　 　　　　(1分)　　 　(2分)

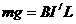
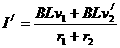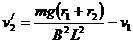cd棒匀速向左运动时　 　　　(1分)　 　　(2分)

(3)不论cd棒向左或向右匀速运动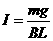

回路的电功率P电=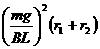　　　　　　　　　　　　　　 (2分)

　　 不论cd棒向左或向右匀速运动，外力的功率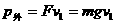　　 (2分)

35、如图所示，两足够长平行光滑的金属导轨MN、PQ相距为L，导轨平面与水平面夹角α＝30°，导轨上端跨接一定值电阻R，导轨电阻不计．整个装置处于方向竖直向上的匀强磁场中，长为L的金属棒cd垂直于MN、PQ放置在导轨上，且与导轨保持电接触良好，金属棒的质量为m、电阻为r，重力加速度为g，现将金属棒由静止释放，当金属棒沿导轨下滑距离为s时，速度达到最大值v_m．求：

(1)金属棒开始运动时的加速度大小；

(2)匀强磁场的磁感应强度大小；

(3)金属棒沿导轨下滑距离为s的过程中，电阻R上产生的电热．

(1)金属棒开始运动时的加速度大小为a，由牛顿第二定律有

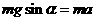　　　　　　　　　　　　　　　　　　　　　　 ①　　　　　　　　　　　 (2分)

解得　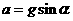 　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　 (2分)

(2)设匀强磁场的磁感应强度大小为B，则金属棒达到最大速度时

产生的电动势　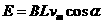 　　　　 ②　　　　　　　　　　　 (1分)

回路中产生的感应电流 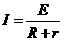　　 ③　　　　　　　　　　　 (1分)

金属棒棒所受安培力　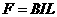 　　　　 ④　　　　　　　　　　　 (1分)

cd棒所受合外力为零时，下滑的速度达到最大，则

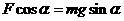　　　　　　　　　　　　　　　　 ⑤　　　 　　　　　　　　 (1分)

由②③④⑤式解得　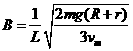 　　　　　　　　　　　　　　　　　　　　　　 (1分)

(3)设电阻R上产生的电热为Q，整个电路产生的电热为Q_总，则

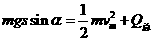　　　　　　　　　　　　 ⑥　　　　　　　　　　　 (3分)

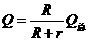　　　　　　　　　　　　　　　　　　　　　　 ⑦　　　　　　　　　　　 (1分)

由⑥⑦式解得　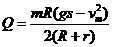 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (1分)

34、如图所示，光滑平行导轨MN、PQ固定于同一水平面内，导轨相距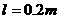，导轨左端接有“0.8V，0.8W”的小灯泡，磁感应强度B＝1T的匀强磁场垂直于导轨平面，导体棒ab与导轨良好接触。导体棒ab在水平拉力作用下沿高贵向右运动，此过程中小灯泡始终正常发光。已知导轨与导体棒每米长度的电阻r=0.5Ω，其余导线电阻不计，导体棒ab的质量m=0.1㎏，ab到左端MP的距离为x。求：

(1)导体棒的速度v与x的关系式；

(2)导体棒从x1=0.1m处运动到x2=0.3m处的过程中水平拉力所做的功。

33、如图所示，小灯泡的规格为“4V　4W”，接在两光滑水平导轨的左端，导轨间距L＝0.5m，电阻不计．金属棒ab垂直搁置在导轨上，电阻r =1Ω，整个装置处于垂直于纸面向里的匀强磁场中，磁感应强度B=1T．为使小灯泡正常发光，求：

(1)金属棒ab匀速滑行的速率；

(2)拉动金属棒ab的外力的功率．

(1)　　　 正常发光时I=P/U 　(1分)

(2)　　　 　I=1A (1分)　　　 灯泡电阻R=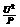 (1分)

　R=4Ω　 (1分)　 E=I(R+r) (1分)　　 E=5V　 (1分)

　 E=BLv　 (1分)　 　　v=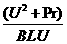 (2分)　　 v=10m/s　 (1分)

(2)由能量守恒可得：P=I²(R+r)　 (3分)　　 P=5w　 (1分)

32、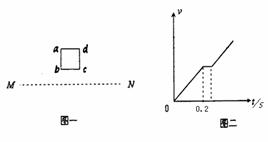如图一所示，abcd是位于竖直平面内的边长为10cm的正方形闭合金属线框，线框的质量为m=0.02Kg，电阻为R=0.1Ω. 在线框的下方有一匀强磁场区域，MN是匀强磁场区域的水平边界，并与线框的bc边平行，磁场方向与线框平面垂直. 现让线框由距MN的某一高度从静止开始下落，经0.2s开始进入磁场,图二是线框由静止开始下落的速度一时间图象。空气阻力不计， g取10m/s²求：

(1)金属框刚进入磁场时的速度；

(2)磁场的磁感应强度；

(1)金属框进入磁场前所做的运动是自由落体运动，

所以：v =gt=10×0.2m/s=2m/s　　　 (4分)

　 (2)在金属框进入磁场的过程中，金属框所受安培力等于重力

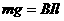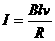　　　　 　　　　　　　　　　　　　　　　 (2分)

　　　　 　　　　　　　　　　　　　　　　 (2分)

　　　　 解得B=0.1T　　　　　　 (2分)

31、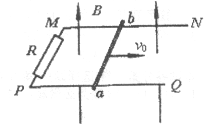如图所示， PQ 、MN 是固定的水平放置的足够长的 U 形金属导轨，导轨的宽度为 L ，整个导轨处于竖直向上、磁感应强度为 B 的匀强磁场中，导轨左端连接一阻值为 R 的电阻器，在导轨上放一质量为 m 的金属棒 ab ，导轨与金属棒电阻均不计，给 ab 一水平初速度 v₀ ，使其向右运动，最后 ab 静止在导轨上， ( 1 )求：当金属棒 ab 的速度为0.5v₀ 时，通过电阻 R 的电流强度．( 2 )针对导轨是光滑还是粗糙的两种情况，小明同学对安培力做功和整个回路中产生的热量进行了如下猜想，即：

猜想 1 ：两种情况下，安培力对金属棒所做的功相等，

猜想 2 ：两种情况下，整个回路产生的热量相等．

你认为以上两种猜想成立吗？请通用计算或相关物理原理解释你的判断．

①I=　　② 简答：不相等；相等。

30、如图(a)，面积S=0.2m²的线圈，匝数n=630匝，总电阻r=1.0Ω，线圈处在变化的磁场中，磁感应强度B随时间t按图(b)所示规律变化，方向垂直线圈平面。图(a)中传感器可看成一个纯电阻R，并标有“3V、0.9W”，滑动变阻器R₀上标有“10Ω、1A”，试回答下列问题：

　 (1)设磁场垂直纸面向外为正方向，试判断通过电流表的电流方向。

　 (2)为了保证电路的安全，求电路中允许通过的最大电流。

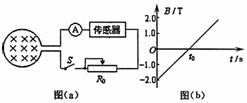　 　 (3)若滑动变阻器触头置于最左端，为了保证电路的安全，图(b)中的t₀最小值是多少？

解：(1)向右

　 (2)传感器正常工作时的电阻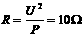

工作电流 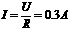　　　(2分)

由于滑动变阻器工作电流是1A，所以电路允许通过的最大电流为I=0.3A　 (1分)

(3)滑动变阻器触头位于最左端时外电路的电阻为R_外=20Ω，故电源电动势的最大值

E=I(R_外+r)=6.3V　 (2分)

由法拉第电磁感应定律

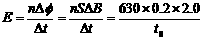　　 (2分)

解得t₀=40s

29、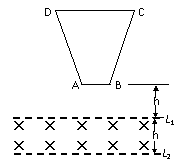如图所示,水平虚线L1、L2之间是匀强磁场,磁场方向水平向里，磁场高度为h。竖直平面内有一等腰梯形线框，底边水平，其上下边长之比为5:1，高为2h。现使线框AB边在磁场边界L1的上方h高处由静止自由下落，当AB边刚进入磁场时加速度恰好为0，在DC边刚进入磁场前的一段时间内，线框做匀速运动。求:

(1)DC边刚进入磁场时，线框的加速度

(2)从线框开始下落到DC边刚进入磁场的过程中，线框的机械能损失和重力做功之比

(1)设AB边刚进入磁场时速度为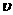₀,线框质量为m、电阻为R，AB=l ,则CD=5 l

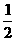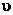则mgh= m₀²　　　　　　　　 (1分)

AB刚进入磁场时有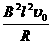， =mg　 (2分)

设线框匀速运动时速度为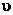₁

E感=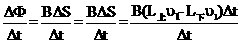=B(2l)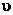₁　 (1分)

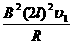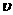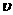线框匀速运动时有=mg；得出₁= ₀/4 (1分)

CD刚进入磁场瞬间，E'_感=B(3l)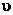₁　 (1分)

　　 F_I=9mg/4　　 (1分)

　a=5g/4　　　　　 (1分)

(2)从线框开始下落到CD边进入磁场前瞬间，根据能量守恒定律得：

　　 mg(3h)-Q= 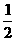m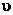₁²　　 (2分)

机械能损失△E=Q= 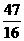mgh　 (1分)

所以，线框的机械能损失和重力做功之比△E：W_G = 47：48　 (1分)

28、如图所示，两根正对的平行金属直轨道MN、M´N´位于同一水平面上，两轨道之间的距离l=0.50m，轨道的MM´端之间接一阻值R=0.40Ω的定值电阻，NN´端与两条位于竖直面内的半圆形光滑金属轨道NP、N´P´平滑连接，两半圆轨道的半径均为R₀=0.50m．直轨道的右端处于竖直向下、磁感应强度B=0.64 T的匀强磁场中，磁场区域的宽度d=0.80m，且其右边界与NN´重合．现有一质量m=0.20kg、电阻r=0.10Ω的导体杆ab静止在距磁场的左边界s=2.0m处．在与杆垂直的水平恒力F=2.0N的作用下ab杆开始运动，当运动至磁场的左边界时撤去F，结果导体杆ab恰好能以最小速度通过半圆形轨道的最高点PP´．已知导体杆ab在运动过程中与轨道接触良好，且始终与轨道垂直，导体杆ab与直轨道之间的动摩擦因数μ=0.10，轨道的电阻可忽略不计，取g=10m/s²，求：

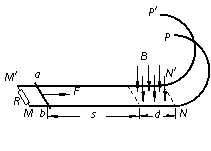(1)导体杆刚进入磁场时，通过导体杆上的电流大小和方向；

(2)导体杆穿过磁场的过程中通过电阻R上的电荷量；

(3)导体杆穿过磁场的过程中整个电路中产生的焦耳热

解：(1)设导体杆在F的作用下运动至磁场的左边界时的速度为v₁，根据动能定理则有　　　　　　

　(F-μmg)s=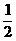mv₁²　 　　　　　　　　　　　　　　　　(2分)　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　

　导体杆刚进入磁场时产生的感应电动势E=Blv₁此时通过导体杆上的电流大小I=E/(R+r)=3.8A(或3.84A)　　　　　　　　　　 (1分)

根据右手定则可知，电流方向为由b向a　　　　　　　　 (1分)

(2)设导体杆在磁场中运动的时间为t，产生的感应电动势的平均值为E_平均，则由法拉第电磁感应定律有　 E_平均=△φ/t=Bld/t 　　　　　　(1分)

通过电阻R的感应电流的平均值 I_平均=E_平均/(R+r)　　　　　 (1分)　　　　

通过电阻R的电荷量 q=It=0.512C(或0.51C)　　　　　　　 (1分)

(3)设导体杆离开磁场时的速度大小为v₂，运动到圆轨道最高点的速度为v₃，因导体杆恰好能通过半圆形轨道的最高点，根据牛顿第二定律对导体杆在轨道最高点时有　　　　　　　　 mg=mv₃²/R₀ 　　　　　　　　(1分)

对于导体杆从NN′运动至PP′的过程，根据机械能守恒定律有

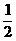mv₂²=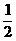mv₃²+mg2R₀ 　　　　　　　　　　　　　　　(2分)

解得v₂=5.0m/s 　　　　　　　　　　　　　　　　　　　(1分)

导体杆穿过磁场的过程中损失的机械能

△E=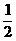mv₁²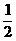_－mv₂²=1.1J 　　　　　　　　　　　　　　　(1分)

此过程中电路中产生的焦耳热为　　 Q=△E-μmgd=0.94J 　　　(2分)