
题目列表(包括答案和解析)
71、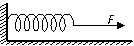 如图所示,一劲度系数为k的轻弹簧,一端固定在竖直的墙上,用手拉住弹簧另一端缓慢地向右拉.试证明在人手拉着弹簧的右端向右移动l距离的过程中,人手克服弹力做的功W=kl2/2.
如图所示,一劲度系数为k的轻弹簧,一端固定在竖直的墙上,用手拉住弹簧另一端缓慢地向右拉.试证明在人手拉着弹簧的右端向右移动l距离的过程中,人手克服弹力做的功W=kl2/2.
由于弹簧的弹力F与弹簧的形变量x成正比.即F=kx.本题中x就是人手向右移动的距离L,因此我们可以建立Fx关系图象( 2分),如图所示.
如果我们将L无限细分成很多相等的小段△x,当△x趋近于零时,则在这一段上的变力F就可以看做恒力.( 2分)
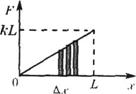 △x与图线所构成的图形为矩形,因此在这段位移△x上弹力所做的功kx·x就等于这个矩形的面积( 2分).
△x与图线所构成的图形为矩形,因此在这段位移△x上弹力所做的功kx·x就等于这个矩形的面积( 2分).
由于功是标量,所以弹力在L的位移内所做的总功就等于各个小段△x上的功(即矩形面积)的总和( 1分).故人手克服弹力所做的功为W=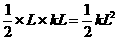 .( 1分)
.( 1分)
70、如图所示,某要乘雪橇从雪坡经A点滑到B点,接着沿水平路面滑至C点停止。人与雪橇的总质量为70kg。右表中记录了沿坡滑下过程中的有关数据,开始时人与雪橇距水平路面的高度h=20m,请根据右表中的数据解决下列问题:
(1)人与雪橇从A到B的过程中,损失的机械能为多少?
(2)设人与雪橇在BC段所受阻力恒定,求阻力的大小。
(3)人与雪橇从B运动到C的过程中所对应的距离。(取g=10m/s2)
|
位置 |
A |
B |
|
||
|
速度(m/s) |
2.0 |
12.0 |
0 |
||
|
时刻(s) |
0 |
4.0 |
10.0 |
解:(1)从A到B的过程中,人与雪橇损失的机械能为
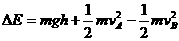 (2分)
(2分)
代入数据解得△E=9.1×103J (1分)
(2)人与雪橇在BC段做减速运动的加速度大小 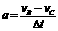 (1分)
(1分)
根据牛顿第二定律有 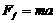 (1分)
(1分)
解得 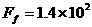 N (2分)
N (2分)
(3)由动能定得得 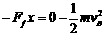 (2分)
(2分)
代入数据解得 x=36m (1分)
69、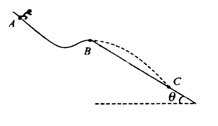 如图所示,质量m=60kg的高山滑雪运动员,从A点由静止开始沿滑雪道滑下,从B点水平飞出后又落在与水平面成倾角
如图所示,质量m=60kg的高山滑雪运动员,从A点由静止开始沿滑雪道滑下,从B点水平飞出后又落在与水平面成倾角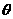 =
=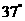 的斜坡上C点.已知AB两点间的高度差为h=25m,B、C两点间的距离为s=75m,已知sin370=0.6,取g=10m/s2,求:
的斜坡上C点.已知AB两点间的高度差为h=25m,B、C两点间的距离为s=75m,已知sin370=0.6,取g=10m/s2,求:
(1)运动员从B点水平飞出时的速度大小;
(2)运动员从A点到B点的过程中克服摩擦力做的功.
解:(1)由B到C平抛运动的时间为t
竖直方向:hBc=ssin37o=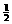 gt2 (1)
(3分)
gt2 (1)
(3分)
水平方向:scos370=vBt (2) (3分)
代得数据,解(1)(2)得vB=20m/s (3)(2分)
(2)A到B过程,由动能定理有
mghAB+wf=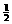 mvB2 (4)
(3分)
mvB2 (4)
(3分)
代人数据,解(3)(4)得 wf =-3000J (2分)
所以运动员克服摩擦力所做的功为3000J
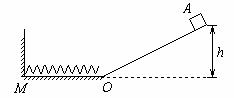
68、如图所示,光滑坡道顶端距水平面高度为h,质量为m的小物块A 从坡道顶端由静止滑下,进入水平面上的滑道,经过O点时无机械能损失,为使A制动,将轻弹簧的一端固定在竖直墙上的M点,另一端恰位于滑道的末端O点。已知在OM段,物块A与水平面间的动摩擦因数均为μ,其余各处的摩擦不计,重力加速度为g,求:
(1)物块滑到O点时的速度大小;
(2)弹簧为最大压缩量d时的弹性势能 (设弹簧处于原长时弹性势能为零)
(3)若物块A能够被弹回到坡道上,则它能够上升的最大高度是多少?
(1)由机械能守恒定律得 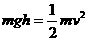 (2分)
(2分)
解得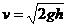 (1分)
(1分)
(2)在水平滑道上物块A克服摩擦力所做的功为
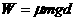 (1分)
(1分)
由能量守恒定律得 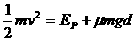 (2分)
(2分)
以上各式联立求解得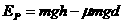 (1分)
(1分)
(3)物块A被弹回的过程中,克服摩擦力所做的功仍为
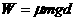 (1分)
(1分)
由能量守恒定律得 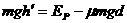 (1分)
(1分)
解得物块A能够上升的最大高度为: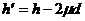 (1分)
(1分)
67、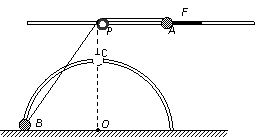 如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg小球A。半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B。用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来。杆和半圆形轨道在同一竖直面内,两小球均可看作质点,且不计滑轮大小的影响,g取10m/s2。现给小球A一个水平向右的恒力F=55N。求:
如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg小球A。半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B。用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来。杆和半圆形轨道在同一竖直面内,两小球均可看作质点,且不计滑轮大小的影响,g取10m/s2。现给小球A一个水平向右的恒力F=55N。求:
(1)把小球B从地面拉到P点正下方C点过程中,力F做的功;
(2)小球B运动到C处时的速度大小;
(3)小球B被拉到离地多高时与小球A速度大小相等。
(1)小球B运动到P点正下方过程中的位移为
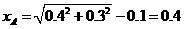 (m)(2分)
(m)(2分)
得:WF=FxA=22J(2分)
(2)由动能定理得
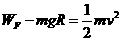
代入数据得:v=4m/s(4分)
⑶当绳与圆环相切时两球的速度相等。
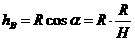 =0.225m(4分)
=0.225m(4分)
66、如图所示,竖直平面内放一直角杆AOB,杆的水平部分粗糙,动摩擦因数=0.20,杆的竖直部分光滑,两部分各套有质量分别为2.0kg和1.0kg的小球A和B,A、B间用细绳相连,初始位置OA=1.5m,OB=2.0m,g取10 m/s2,则
(1)若用水平拉力F1沿杆向右缓慢拉A,使之移动0.5m,该过程中A受到的摩擦力多大?拉力F1做功多少?
(2)若小球A、B都有一定的初速度,A在水平拉力F2的作用下,使B由初始位置以1.0m/s的速度匀速上升0.5m,此过程中拉力F2做功多少?
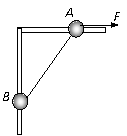

(1)A、B小球和细绳整体竖直方向处于平衡,A受到水平的弹力为:
N=(mA+mB)g (2分)
则A受到的摩擦力为Ff=(mA+mB)g
代入数字得:Ff=6N (2分)
由几何关系,sB=0.5m (2分)
由能量关系,拉力F1做功为:
W1=Ffs+mBgsB;
代入数字得:W1=20 J (2分)
(2)设细绳与竖直方向的夹角为,因细绳不可伸长,所以有
vBcos=vAsin (2分)
则: m/s
m/s
 m/s (2分)
m/s (2分)
设拉力F2做功为W2,对系统由能量关系得:
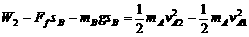 (2分)
(2分)
代入数字得W2=6.8 J (2分)
65、如图所示,电场极板AB间有电场强度 的匀强电场,一带电量
的匀强电场,一带电量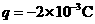 的小球开始时静止在电场中的
的小球开始时静止在电场中的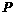 点,靠近电场极板B处有一挡板S,小球与挡板S的距离
点,靠近电场极板B处有一挡板S,小球与挡板S的距离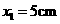 ,与
,与 板距离
板距离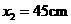 ,小球的重力不计.在电场力作用下小球向左运动,与挡板S相碰后电量减少到碰前的K倍,已知
,小球的重力不计.在电场力作用下小球向左运动,与挡板S相碰后电量减少到碰前的K倍,已知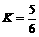 ,碰撞过程中小球的机械能没有损失.
,碰撞过程中小球的机械能没有损失.
(1)求小球第一次到达挡板S时的动能;
(2)求小球第一次与挡板S相碰后向右运动的距离;
(2)小球与挡板S经过多少次碰撞后,才能运动到 板?
板?
解:(1)小球第一次到达挡板时,由动能定理得
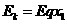 =0.02J
(3分)
=0.02J
(3分)
(2)设小球与挡板相碰后向右运动s,则
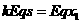 (2分)
(2分)
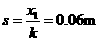 (1分)
(1分)
(3)分析题意可知,每次碰后向右运动的距离是前一次的1/k,
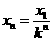
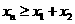 (4分)
(4分)
n=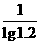 =13
(2分)
=13
(2分)
64、如图所示,一倾角为30°的光滑斜面底端有一与斜面垂直的固定挡板M,物块A、B之间用一与斜面平行轻质弹簧连结,现用力缓慢沿斜面向下推动物块B,当弹簧具有5J弹性势能时撤去推力释放物块B;已知A、B质量分别为mA=5kg、mB=2kg,弹簧的弹性势能表达式为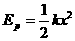 ,其中弹簧的劲度系数k=
,其中弹簧的劲度系数k= ,x为弹簧形变量,
,x为弹簧形变量,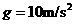 ,求:
,求:
(1)当弹簧恢复原长时,物块B的速度大小;
(2)物块A刚离开挡板时,物块B的动能.
解:(1)当Ep =5J时,弹簧压缩x1,由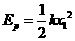 得x1=0.1m
(2分)
得x1=0.1m
(2分)
当弹簧恢复原长时,由机械能守恒可得
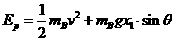 (2分)
(2分)
v=2m/s (1分)
(2)当物块A刚离开挡板时,弹簧伸长x2,
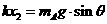 (1分)
(1分)
x2=0.025m (1分)
由系统机械能守恒得
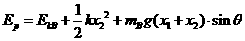 (2分)
(2分)
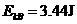 (1分)
(1分)
63、当空间探测器从行星旁绕过时,由于行星的引力作用,将“偷”取一部分行星的能量,可以使探测器的运动速率增大,这种现象被称之为“弹弓效应”。在航天技术中,“弹弓效应”是用来增大人造小天体运动速率的一种有效方法。1997年10月15日发射升空的卡西尼号宇宙飞船在到达土星前,就是这样“偷’’了两次金星、一次地球的引力使自己加速,直奔土星,当然中途经过巨大的木星更不会放过,照例再“偷”一次。右图就是“弹弓效应”示意图:质量为m的空间探测器以相对于太阳的速度v0飞向质量为M的行星,此时行星相对于太阳的速度u0,探测器绕过行星后相对于太阳的速度为v,,此时行星相对于太阳的速度为u,且m<M,v0、v、u0、u的方向均可视为相互平行。
(1)试写出探测器与行星构成的系统在上述过程中“动量守恒”及“始末状态总动能相等”的方程,并在m<M的条件下,用v0和u0来表示v;
(2)若上述行星是质量为M=5.67×l026kg的土星,其相对于太阳的轨道速率u0=9.6 km/s,而空间探测器的质量m=150 kg,相对于太阳迎向土星的速率v0=10.4 km/s,则由于 “弹弓效应”,该探测器绕过土星后沿与原来速度相反的方向离去,求它离开土星后相对太阳的速率增为多少?
(3)若此探测器飞向行星时其速度v0与土星的速度u0同方向,则是否仍能产生使探测器速率增大的“弹弓效应”,简要说明理由。
解:(1)动量守恒的方程为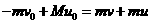 ①
①
始末状态总动能相等的方程为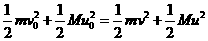 ②
②
解得: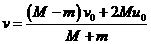 ,当
,当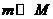 时,
时,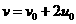 ③
③
(2)代入数据得: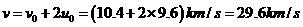
(3)不能。根据如下:
由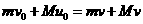 与
与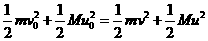 得
得
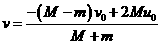 ,故当
,故当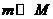 时,
时,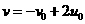 。而
。而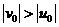 ,故
,故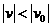 ,不能使探测器速度增大。
,不能使探测器速度增大。
评分标准:(1)(12分)写出①②③两式各得4分;(2)(5分)解出v=29.6km/s,得5分;(3)(5分)判断出不能使探测器速度增大并理由充分得5分,否则酌情扣分。
62、如图所示,挡板P固定在足够高的水平桌面上,小物块A和B大小可忽略,它们分别带有+QA和+QB的电荷量,质量分别为mA和mB.两物块由绝缘的轻弹簧相连,一不可伸长的轻绳跨过滑轮,一端与B连接,另一端连接一轻质小钩,整个装置处于方向水平向左的匀强电场中,电场强度为E.开始时A、B静止,已知弹簧的劲度系数为k,不计一切摩擦及A、B间的库仑力,A、B所带电荷量保持不变,B一直在水平面上运动且不会碰到滑轮.试求
(1) 开始A、B静止时,挡板P对物块A的作用力大小;
(2) 若在小钩上挂一质量为M的物块C并由静止释放,当物块C下落到最大距离时物块A对挡板P的压力刚好为零,试求物块C下落的最大距离;
(3) 若C的质量改为2M,则当A刚离开挡板P时,B的速度多大?

解析:(15分)(1)对系统AB:
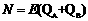 (4分)
(4分)
(2)开始时弹簧形变量为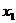 ,由平衡条件:
,由平衡条件: ①(2分)
①(2分)
设当A刚离开档板时弹簧的形变量为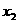 :由:
:由: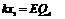 可得
可得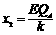 ②(2分)
②(2分)
故C下降的最大距离为: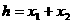 ③……………(1分)
③……………(1分)
由①-③式可解得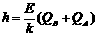 ④……………
(1分)
④……………
(1分)
(3)由能量守恒定律可知:C下落h过程中,C重力势能的的减少量等于B的电势能的增量和弹簧弹性势能的增量以及系统动能的增量之和
当C的质量为M时: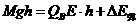 ⑤…(2分)
⑤…(2分)
当C的质量为2M时,设A刚离开挡板时B的速度为V
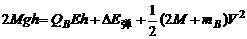 ⑥ …(2分)
⑥ …(2分)
由④-⑥式可解得A刚离开P时B的速度为:
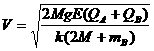 ⑦………………(1分)
⑦………………(1分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com