1．5×10^{－8 cm}　1.62×10^{－8 cm}　1.42×10^{－8 cm}

其平均值为：＝＝1.51×10^{－10 m}

这与公认值的数量相吻合，故本次估测数值符合数量级的要求．

答案：4×10^－3　8×10^－6　1.5×10^－8　1.62×10^－8　1.42×10^－8　1.51×10^{－10 m}　符合要求

4．在用油膜法估测分子的大小实验中，已知一滴溶液中油酸的体积为V_油酸，配制的油酸溶液中，纯油酸与溶液体积之比为1∶500,1 mL溶液滴250滴，那么1滴溶液的体积是________mL，所以一滴溶液中油酸体积为V_油酸＝________cm³.若实验中测得结果如下表所示，请根据所给数据填写出空白处的数值，并与公认的油酸分子长度值L₀＝1.12×10^{－10 m}作比较，并判断此实验是否符合数量级的要求.

解析：由题给条件得，1滴溶液的体积为V_溶液＝ mL＝4×10^－3 mL，因为＝，故1滴溶液中油酸体积为：

V_油酸＝V_溶液＝× cm³＝8×10^{－6 cm3}.

据此算得3次测得L的结果分别为：

3．用油膜法估测油酸分子的大小，实验器材有：浓度为0.05%(体积分数)的油酸酒精溶液、最小刻度为0.1 mL的量筒、盛有适量清水的45×50 cm²浅盘、痱子粉、橡皮头滴管、玻璃板、彩笔、坐标纸．

(1)下面是实验步骤，请填写所缺的步骤C

A．用滴管将浓度为0.05%油酸酒精溶液一滴一滴地滴入量筒中，记下滴入1 mL油酸酒精溶液时的滴数N.

B．将痱子粉均匀地撒在浅盘内水面上，用滴管吸取浓度为0.05%的油酸酒精溶液，从低处向水面中央一滴一滴地滴入，直到油酸薄膜有足够大的面积又不与器壁接触为止，记下滴入的滴数n.

C．________________________________________________________________________.

D．将画有油酸薄膜轮廓的玻璃板放在坐标纸上，以坐标纸上边长为1 cm的正方形为单位，计算轮廓内正方形的个数，算出油酸薄膜的面积S.

(2)用已给的和测得的物理量表示单个油酸分子的直径大小________(单位：cm)．

解析：(1)将玻璃板放在浅盘上，用彩笔将油酸薄膜的形状画在玻璃板上．

(2)1滴油酸溶液中含有的油酸体积为 mL，向浅盘中共滴入油酸的体积V＝ cm³，所以单个油酸分子的直径为d＝＝ cm.

答案：(1)将玻璃板放在浅盘上，用彩笔将油酸薄膜的形状画在玻璃板上　(2) cm

2．在用油膜法估算分子大小的实验中：

(1)下面是一些实验步骤及注意事项：

A．在准备实验时，油酸酒精溶液要提前一天配制，以免因溶液不均匀产生误差；

B．一定要仔细清洗浅盘，充分洗去油污、粉尘，以免给实验带来误差；

C．用注射器(或滴管)将V＝1 毫升油酸酒精溶液一滴一滴的滴入量筒中，并记下滴数n，计算出每滴油酸酒精溶液的平均体积V₀＝；

D．向浅盘里注入适量的水，并将痱子粉(或石膏粉)从盘的中央加入，使粉扩散至均匀，再用注射器(或滴管)从适当高处将一滴油酸酒精溶液滴在水面上；

E．等待油酸薄膜的形状稳定后，用数格子法测算出面积S；

F．根据一滴油酸酒精溶液的体积V₀和膜的面积S计算出油酸薄膜的厚度L＝；

G．重复实验测几次油酸薄膜的厚度并求出平均值，即可认为就是油酸分子的直径．

其中错误的是：__________；不必要的是：__________(只填前面的字母)．

(2)这个实验中产生误差的主要原因有：_

_______________________________________________________________________

________________________________________________________________________.

答案：(1)F　A

(2)计算一滴油酸酒精溶液中含纯油酸的体积时，由于一滴油酸酒精溶液的体积和浓度测不准产生误差；用数格子法求油酸薄膜的面积本身就是一种估算方法

1．把V₁ mL的油酸倒入适量的酒精中，稀释成V₂ mL的油酸酒精溶液，测出1 mL油酸酒精溶液共有N滴．取一滴溶液滴入水中，最终在水中形成S cm²的单分子油膜．则该油酸分子的直径大约为(　)

A. m　 　　B. m　 　　C. cm　 　　D. cm

答案：D

6．

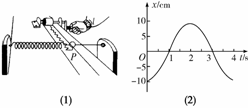
图1－1－18

　 简谐运动的振动图线可用下述方法画出：如图1－1－18(1)所示，在弹簧振子的小球上安装一枝绘图笔P，让一条纸带在与小球振动方向垂直的方向上匀速运动，笔P在纸带上画出的就是小球的振动图象．取振子水平向右的方向为振子离开平衡位置的位移正方向，纸带运动的距离代表时间，得到的振动图线如图1－1－18(2)所示．

(1)为什么必须匀速拖动纸带？

(2)刚开始计时时，振子处在什么位置？t＝17 s时振子相对平衡位置的位移是多少？

(3)若纸带运动的速度为2 cm/s，振动图线上1、3两点间的距离是多少？

(4)振子在______ s末负方向速度最大；在______ s末正方向加速度最大；2.5 s时振子正在向______方向运动．

(5)写出振子的振动方程．

解析：(1)纸带匀速运动时，由x＝vt知，位移与时间成正比，因此在匀速条件下，可以用纸带通过的位移表示时间．

(2)由图(2)可知t＝0时，振子在平衡位置左侧最大位移处；周期T＝4 s，t＝17 s时位移为零．

(3)由x＝vt，所以1、3间距x＝2 cm/s×2 s＝4 cm.

(4)3 s末负方向速度最大；加速度方向总是指向平衡位置，所以t＝0或t＝4 s时正方向加速度最大；t＝2.5 s时，向－x方向运动．

(5)x＝10sin cm

答案：(1)在匀速条件下，可以用纸带通过的位移表示时间

(2)左侧最大位移　零　(3)4 cm　(4)3　0或4　－x　(5)x＝10sin cm

5.

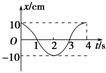
图1－1－17

　 根据如图1－1－17所示的振动图象：

(1)算出下列时刻振子对平衡位置的位移．

①t₁＝0.5 s；②t₂＝1.5 s

(2)将位移随时间的变化规律写成x＝Asin(ωt+φ)的形式并指出振动的初相位是多少？

解析：(1)由图象可知A＝10 cm，T＝4 s

故位移：x＝Acos ωt＝10cos t＝10cos t cm

①当t₁＝0.5 s时，x₁＝5 cm

②当t₂＝1.5 s时，x₂＝－5 cm

(2)振子的位移表达式为：x＝10cos t＝10sincm，初相位为：φ＝.

答案：(1)①5 cm　②－5 cm　(2)x＝10sincm　

4.

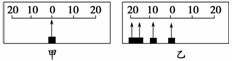
图1－1－16

　 (2010·朝阳区模拟)如图1－1－16所示为用频闪照相的方法拍到的一个水平放置的弹簧振子振动情况．甲图是振子静止在平衡位置的照片，乙图是振子被拉伸到左侧距平衡位置20 mm处，放手后向右运动周期内的频闪照片．已知频闪的频率为10 Hz.求：

(1)相邻两次闪光的时间间隔t₀、振动的周期T₀.

(2)若振子的质量为20 g，弹簧的劲度系数为50 N/m，则振子的最大加速度是多少？

解析：(1)T＝＝0.1 s，即相邻两次闪光的时间间隔为t₀＝0.1 s．振子从最大位移处运动到平衡位置经历时间为0.3 s，故振子振动周期T₀＝1.2 s.

(2)a_m＝＝＝50 m/s²

答案：(1)0.1 s　1.2 s　(2)50 m/s²

3.　

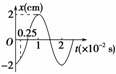
图1－1－15

　 一质点做简谐运动，其位移和时间关系如图1－1－15所示．

(1)求t＝0.25×10^－2 s时的位移；

(2)在t＝1.5×10^－2 s到2×10^－2 s的振动过程中，质点的位移、回复力、速度、动能、势能如何变化？

(3)在t＝0至8.5×10^－2 s时间内，质点的路程、位移各多大？

解析：(1)由图可知A＝2 cm，T＝2×10^－2 s，

振动方程为x＝Asin＝－Acos ωt＝－2cos t cm＝－2cos(10²πt) cm

当t＝0.25×10^－2 s时x＝－2cos cm＝－ cm.

(2)由图可知在1.5×10^－2 s-2×10^－2 s内，质点的位移变大，回复力变大，速度变小，动能变小，势能变大．

(3)从t＝0至8.5×10^－2 s的时间内质点的路程为s＝17A＝34 cm，位移为2 cm.

答案：(1)－ cm　(2)位移变大，回复力变大，速度变小，动能变小，势能变大　(3)34 cm　2 cm

2．

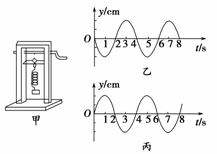
图1－1－14

　 一砝码和一轻弹簧构成弹簧振子，如图1－1－14甲所示，该装置可用于研究弹簧振子的受迫振动．匀速转动把手时，曲杆给弹簧振子驱动力，使振子做受迫振动．把手匀速转动的周期就是驱动力的周期，改变把手匀速转动的速度就可以改变驱动力的周期．若保持把手不动，给砝码一向下的初速度，砝码便做简谐运动，振动图线如图1－1－14乙所示．当把手以某一速度匀速转动，受迫振动达到稳定时，砝码的振动图象如图1－1－14丙所示．若用T₀表示弹簧振子的固有周期，T表示驱动力的周期，Y表示受迫振动达到稳定后砝码振动的振幅，则

(1)稳定后，物体振动的频率f＝________ Hz.

(2)欲使物体的振动能量最大，需满足什么条件？

答：________________________________________________________________________.

(3)利用上述所涉及的知识，请分析某同学所提问题的物理道理．

“某同学考虑，我国火车第六次大提速时，需尽可能的增加铁轨单节长度，或者是铁轨无结头”．

答：________________________________________________________________________.

解析：(1)由丙图可知，f＝＝ Hz＝0.25 Hz.

(2)物体振动能量最大时，即振幅最大，故应发生共振，所以应有T＝T₀＝4 s.

(3)若单节车轨非常长，或无结头，则驱动力周期非常大，从而远离火车的固有周期，即火车的振幅较小．以便来提高火车的车速．

答案：(1)0.25　(2)T＝T₀＝4 s

(3)远离火车的固有周期，以便于提高火车的车速