
题目列表(包括答案和解析)
5. 假如一个做匀速圆周运动的人造地球卫星的轨道半径增大到原来的2倍,仍做匀速圆周运动,则( )
A. 根据公式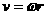 ,可知卫星的线速度增大到原来的2倍
,可知卫星的线速度增大到原来的2倍
B. 根据公式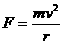 ,可知卫星所需的向心力减小到原来的
,可知卫星所需的向心力减小到原来的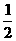
C. 根据公式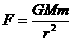 ,可知地球提供的向心力将减小到原来的
,可知地球提供的向心力将减小到原来的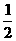
D. 根据上述B和A给出的公式,可知卫星的线速度将减小到原来的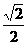
4. 设行星绕恒星运动轨道为圆形,则由开普勒第三定律可知它运动的周期平方与轨道半径的三次方之比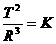 为常数,此常数的大小( )
为常数,此常数的大小( )
A. 只与恒星质量有关
B. 与恒星质量和行星质量均有关
C. 只与行星质量有关
D. 与恒星质量和行星质量均无关
3. 设想人类开发月球,不断把月球上的矿藏搬运到地球上,假定经过长时间开采后,地球仍可当作均匀球体,月球仍旧沿开采前的圆周轨道运动,则与开采前相比( )
A. 地球与月球间的万有引力将不变
B. 地球与月球间的万有引力将变大
C. 月球绕地球运动的周期将变大
D. 月球绕地球运动的周期将变短
2. 下列关于万有引力的说法,正确的有( )
A. 物体落在地面上,说明地球对物体有引力,物体对地球没有引力
B. 万有引力定律是牛顿看到苹果落地而想到的
C. 地面上自由下落的苹果和天空中运行的月亮,受到的都是地球的万有引力
D. 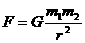 中的G是一个比例常数,是没有单位的
中的G是一个比例常数,是没有单位的
当卫星进入轨道前加速的过程中,卫星上的物体(包括卫星本身)处于超重状态,此情景与“升降机”中物体的超重相同。当卫星进入轨道后正常运转时,卫星上的物体处于完全“失重”状态(因为重力刚好提供向心力),因此,在卫星上的仪器,凡是制造原理与重力有关的均不能正常使用。
[例12] 某一物体在地球表面时,由弹簧测力计测得重160N,把此物体放在航天器中,若航天器以加速度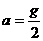 (
(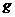 为地球表面的重力加速度)垂直地面上升,这时再用同一弹簧测力计测得物体的重力为90N,忽略地球自转的影响,已知地球半径R,求此航天器距地面的高度。
为地球表面的重力加速度)垂直地面上升,这时再用同一弹簧测力计测得物体的重力为90N,忽略地球自转的影响,已知地球半径R,求此航天器距地面的高度。
解析:物体在地球表面时,重力为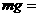 160N ①
160N ①
根据万有引力定律,在地面附近有
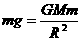 ②
②
在距地面某一高度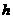 时,由牛顿定律得
时,由牛顿定律得
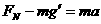 ③
③
根据万有引力定律,得
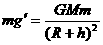 ④
④
由①②③④式并代入数据解得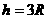 。
。
点评:人造卫星在轨道上运行时,处于完全失重状态;人造卫星发射、回收时,加速度均向上,处于超重状态。
[模拟试题]
1. 16世纪,哥白尼根据天文观测的大量资料,经过40多年的天文观测和潜心研究,提出“日心说”的如下四个基本论点,这四个论点目前看不存在缺陷的是( )
A. 宇宙的中心是太阳,所有行星都在绕太阳做匀速圆周运动
B. 地球是绕太阳做匀速圆周运动的行星,月球是绕地球做匀速圆周运动的卫星,它绕地球运转的同时还跟地球一起绕太阳运动
C. 天穹不转动,因为地球每天自西向东自转一周,造成天体每天东升西落的现象
D. 与日地距离相比,恒星离地球都十分遥远,比日地间的距离大得多
相对地面静止的卫星为地球同步卫星,又称通讯卫星。同步卫星的周期为地球自转的周期,即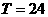 小时,其轨道一定在赤道平面内,高度
小时,其轨道一定在赤道平面内,高度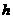 一定,
一定,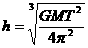
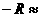
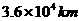 。所以同步卫星都位于同一轨道的不同位置上。
。所以同步卫星都位于同一轨道的不同位置上。
[例11] 用 表示地球通讯卫星(同步卫星)的质量,
表示地球通讯卫星(同步卫星)的质量,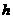 表示它离地面的高度,
表示它离地面的高度,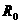 表示地球的半径,
表示地球的半径,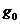 表示地球表面处的重力加速度,
表示地球表面处的重力加速度,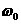 表示地球自转角速度,则通讯卫星所受的地球对它的万有引力的大小为( )
表示地球自转角速度,则通讯卫星所受的地球对它的万有引力的大小为( )
A. 等于零 B.
等于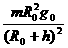
C. 等于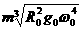 D.
以上结果都不对
D.
以上结果都不对
解析:通讯卫星所受万有引力的大小为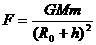
地球表面物体的重力可以认为等于万有引力,即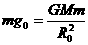 ,故
,故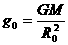
由上两式解得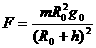 。显然B是正确的。
。显然B是正确的。
由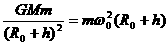 ,即
,即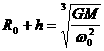
可得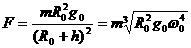 ,
,
即C也正确。故本题正确的答案是BC。
点评:利用万有引力提供向心力和地球表面物体的重力约等于万有引力这两个基本思路,是解决天体问题的关键。
卫星绕地球稳定运行时,万有引力提供了卫星做圆周运动的向心力,由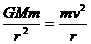 ,得
,得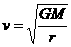 ,由此可知,轨道半径
,由此可知,轨道半径 越大,卫星的线速度
越大,卫星的线速度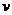 越小,当卫星由于某种原因速度
越小,当卫星由于某种原因速度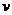 发生改变时,受到的万有引力
发生改变时,受到的万有引力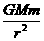 和需要的向心力
和需要的向心力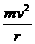 不再相等,卫星将偏离原轨道运动。当
不再相等,卫星将偏离原轨道运动。当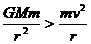 时,卫星做近心运动,其轨道半径
时,卫星做近心运动,其轨道半径 减小,由于万有引力做功,因而速度
减小,由于万有引力做功,因而速度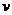 越来越大。反之,当
越来越大。反之,当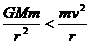 时,卫星做离心运动,其轨道半径
时,卫星做离心运动,其轨道半径 增加,速度
增加,速度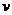 越来越小。
越来越小。
[例9] 在半径为 的轨道上做匀速圆周运动的卫星,它所具有的机械能为E,动能为
的轨道上做匀速圆周运动的卫星,它所具有的机械能为E,动能为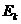 ,由于一种原因使它的速度突然增大,则当它重新稳定下来做匀速圆周运动时,有( )
,由于一种原因使它的速度突然增大,则当它重新稳定下来做匀速圆周运动时,有( )
A.  增大,E增大,
增大,E增大,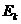 增大
增大
B.  增大,E增大,
增大,E增大,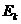 减小
减小
C.  减小,E增大,
减小,E增大,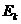 减小
减小
D.  减小,E减小,
减小,E减小,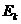 增大
增大
解析: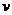 增大时,说明外界对其做正功,故它的机械能E增大,卫星将表现离心现象,轨道半径将增大,万有引力做负功,动能减小,势能增大,故应选B。
增大时,说明外界对其做正功,故它的机械能E增大,卫星将表现离心现象,轨道半径将增大,万有引力做负功,动能减小,势能增大,故应选B。
点评:卫星的运动分为稳定和不稳定运行,当其所受的万有引力不刚好提供向心力时,其速度和半径就要发生变化,引力要做功,这为不稳定运行;而当所受的引力刚好提供向心力时,它运行的速度、轨道半径确定不变而做匀速圆周运动,这种状态称为稳定运行。对于稳定运行,应从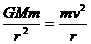 入手,应用匀速圆周运动知识分析;对于不稳定运行的卫星问题(变轨问题)应从做功、能量转化的角度去分析处理。
入手,应用匀速圆周运动知识分析;对于不稳定运行的卫星问题(变轨问题)应从做功、能量转化的角度去分析处理。
由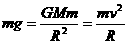 ,得近地人造卫星的环绕速度
,得近地人造卫星的环绕速度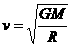
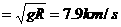 。通常称为第一宇宙速度,也是人造卫星的最小发射速度。
。通常称为第一宇宙速度,也是人造卫星的最小发射速度。
由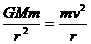 ,得不同高度处的人造卫星的环绕速度
,得不同高度处的人造卫星的环绕速度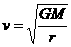 ,其大小随半径的增大而减小。但是,由于在人造地球卫星发射过程中火箭要克服地球引力做功,所以将卫星发射到离地球越远的轨道,在地面上所需的发射速度就越大。
,其大小随半径的增大而减小。但是,由于在人造地球卫星发射过程中火箭要克服地球引力做功,所以将卫星发射到离地球越远的轨道,在地面上所需的发射速度就越大。
3. 由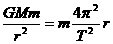 ,得
,得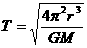
故 越大,T越大。
越大,T越大。
[例8] 火星有两颗卫星,分别为火卫一和火卫二,它们的轨道近似为圆,已知火卫一的周期为7小时39分,火卫二的周期为30小时18分,则两颗卫星( )
A. 火卫一距火星表面较近
B. 火卫二的角速度较大
C. 火卫一的运动速度较大
D. 火卫二的向心加速度较大
解析:由万有引力提供向心力得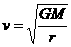 ,
,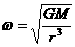 ,
,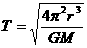 ,
,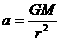 。可见
。可见 越大,
越大,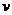 越小,
越小, 越小,T越大,即转得越慢,因火卫二相对转得较慢,周期大,故线速度小、角速度小、向心加速度小,所以选A和C。
越小,T越大,即转得越慢,因火卫二相对转得较慢,周期大,故线速度小、角速度小、向心加速度小,所以选A和C。
点评:本题关键是从万有引力提供卫星做匀速圆周运动的向心力入手,明确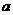 、
、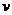 、
、 、T与轨道半径
、T与轨道半径 的关系,再由周期大小,判断该题的正确答案。
的关系,再由周期大小,判断该题的正确答案。
2. 由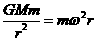 ,得
,得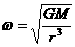
故 越大,
越大, 越小;
越小;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com