
题目列表(包括答案和解析)
1. 重力势能是物体和地球这一系统共同所有,单独一个物体谈不上具有势能。即:如果没有地球,物体谈不上有重力势能,平时说物体具有多少重力势能,是一种习惯上的简称。
4. 关于动能与动量的比较
(1)动能与动量都是由质量和速度共同决定的物理量;
(2)动能和动量都是用于描述物体机械运动的状态量;
(3)动能是标量,动量是矢量;
(4)动能决定了物体克服一定阻力能运动多远,动量则决定着物体克服一定阻力能运动多长时间;
(5)动能是从能量观点出发描述机械运动的,动量是从机械运动本身出发描述机械运动状态的。
例3:总质量为M的列车,沿水平直线轨道匀速前进,其末节车厢质量为m,中途脱钩,司机发觉时,机车已行驶了L距离,于是立即关闭油门撤去牵引力。设运动的阻力与质量成正比,比例系数为k,机车的牵引力恒定,当列车的两部分都停止时,它们的距离是多少?
析与解:设牵引力为F,脱钩前列车的速度为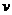 ,脱钩后两部分的位移分别为
,脱钩后两部分的位移分别为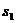 、
、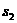 。对列车脱钩到静止的全过程,由动能定理:
。对列车脱钩到静止的全过程,由动能定理: ,对末节车厢,脱钩后运动的全过程,由动能定理:
,对末节车厢,脱钩后运动的全过程,由动能定理: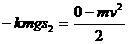 ,由脱钩前列车匀速运动得:
,由脱钩前列车匀速运动得: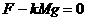 ,解得:
,解得: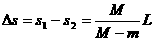 。
。
本题也可用补偿法进行分析。若末节车厢脱钩时司机关闭油门,则两部分运动情况完全相同,停止时它们的距离为0,脱钩后牵引力做了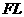 的功,才使两部分拉开距离,这部分功补偿机车多行驶距离中克服阻力所做的功。
的功,才使两部分拉开距离,这部分功补偿机车多行驶距离中克服阻力所做的功。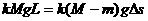 ,所以
,所以 。
。
点评:本题还可以用运动学知识与牛顿第二定律求解,但较繁杂,显然,用补偿法求解则简单快捷,所以平时做题要注意进行解题方法总结。
3. 应用动能定理的注意点:
(1)明确研究对象、研究过程,找出初、末状态的速度情况。
(2)要对物体进行正确的受力分析(包括重力),明确各力做功的大小及正负情况。
(3)若物体运动过程中包含几个不同物理过程,解题时,可以分段考虑,也可视为一整体过程,列出动能定理求解。
2. 外力对物体做功与物体动能的关系:
外力对物体做正功,物体的动能增加,这一外力有助于物体的运动,是动力;外力对物体做负功,物体的动能减小,这一外力是阻碍物体的运动,是阻力,外力对物体做负功往往又称物体克服阻力做功。功是能量转化的量度,外力对物体做了多少功;就有多少动能与其他形式的能发生了转化。所以外力对物体所做的功就等于物体动能的变化量,即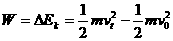 。这就是动能定理。
。这就是动能定理。
1. 动能是一个状态量,它与物体的运动状态对应。动能也是标量,它只有大小,没有方向,而且物体的动能总是大于等于零,不会出现负值。
动能具有相对性,它与参照物的选取有关。如:在行驶中汽车上的物体,对汽车上的乘客,物体动能为零;但对路边的行人,物体的动能不为零。
3. 机车的两种启动
(1)机车以恒定功率启动,牵引力随速度的增大而减小,机车做加速度逐渐减小的变加速运动。当加速度减小到零时速度最大,以后机车做匀速运动(牵引力等于阻力)。如图3所示机车以恒定功率启动的P-t图和v-t图。(机车在水平面运动,阻力视为恒定)
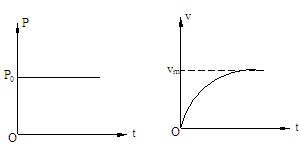
图3
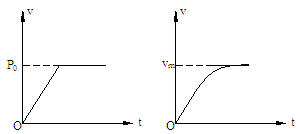
图4
(2)机车匀加速启动,机车先做初速为零的匀加速运动。功率随时间正比例增大,当增大到额定功率时,开始做一段变加速运动,牵引力减小到等于阻力时,机车的速度增大到最大速度。如图4为机车以匀变速启动的P-t和v-t图。
例2:汽车发动机的额定牵引功率为60kW,汽车质量为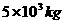 ,汽车在水平路面上行驶时,阻力是车重的
,汽车在水平路面上行驶时,阻力是车重的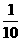 倍,试问(取
倍,试问(取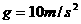 ):
):
(1)汽车保持以额定功率从静止起动后能达到的最大速度是多少?
(2)若汽车从静止开始,保持以 的加速度做匀加速直线运动,这一过程能维持多长时间?
的加速度做匀加速直线运动,这一过程能维持多长时间?
析与解:
(1)汽车一开始就保持额定功率,牵引力随速度的增大而减小,汽车做加速度逐渐减小的变加速运动,当加速度减小到零时速度最大。
此时,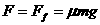 ,
,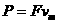
所以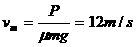
(2)汽车以恒定加速度起动,先做初速为零的匀加速运动,功率随时间正比例增大,当增大到额定功率时,开始做变加速运动。设保持匀加速运动的时间为t,匀加速运动能达到的最大速度为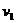 ,则:
,则:
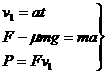 ,所以
,所以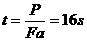
2. 对力的功率的认识
由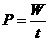 、
、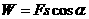 可得:
可得: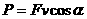 ,此式中
,此式中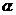 为力F与速度
为力F与速度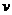 之间的夹角。把
之间的夹角。把 当作整体来看是物体在力的方向上的分速度,即:作用在物体上的力与物体在力的方向上分速度的乘积叫做力的功率。
当作整体来看是物体在力的方向上的分速度,即:作用在物体上的力与物体在力的方向上分速度的乘积叫做力的功率。
对一个动力机械,当功率P一定时,由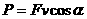 可知:降低运动速度可以增大牵引力;反过来,若阻力很小,可以加快运动速度。这一点在各种机械设备中有着广泛的应用。
可知:降低运动速度可以增大牵引力;反过来,若阻力很小,可以加快运动速度。这一点在各种机械设备中有着广泛的应用。
任何机械都有一个铭牌,铭牌上所注功率为这部机械的额定功率。它是提供人们对机械进行选择、配置的一个重要参数,它反映了机械的做功能力或机械所能承担的“任务”。机械运行过程中的功率是实际功率。机械的实际功率可以小于其额定功率(俗称机械没吃饱),可以等于其额定功率(称满负荷运行),还可以在短时间内略大于其额定功率(称超负荷运行)。机械不能长时间超负荷运行,那样会损坏机械设备,缩短其使用寿命。
1. 功率是描述做功快慢的物理量
由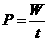 可知,功率的大小只与其“比值”有直接联系,与做功多少和时间长短无直接关联,比较功率的大小就要比较功与完成这些功的所用时间之“比值”。“比值”大,功率就大,做功就快,“比值”小,功率就小,做功就慢。
可知,功率的大小只与其“比值”有直接联系,与做功多少和时间长短无直接关联,比较功率的大小就要比较功与完成这些功的所用时间之“比值”。“比值”大,功率就大,做功就快,“比值”小,功率就小,做功就慢。
物体做功功率是描述物体做功的一个状态;做功的多少是一个过程,所以不能说功率大,做功就多。物体做功多少是做功物体在做功过程中的一个积累,随着做功过程的积累时间越长,这个物体做功就越多,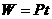 就是一个积累的意思。即P在时间t上的积累就是物体做功的多少。
就是一个积累的意思。即P在时间t上的积累就是物体做功的多少。
4. 对功的物理含义的理解
关于功我们不仅要从定义式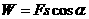 进行理解和计算,还应理解它的物理含义。功是能量转化的量度,即:做功的过程是能量的一个转化过程,这个过程做了多少功,就是多少能量发生了转化。对物体做正功,物体的能量增加。对物体做了多少正功,物体的能量就增加了多少;对物体做负功,也称物体克服阻力做功,物体的能量减少,做了多少负功,物体的能量就减少了多少。因此功的正、负表示能的转化情况,表示物体是输入了能量还是输出了能量。
进行理解和计算,还应理解它的物理含义。功是能量转化的量度,即:做功的过程是能量的一个转化过程,这个过程做了多少功,就是多少能量发生了转化。对物体做正功,物体的能量增加。对物体做了多少正功,物体的能量就增加了多少;对物体做负功,也称物体克服阻力做功,物体的能量减少,做了多少负功,物体的能量就减少了多少。因此功的正、负表示能的转化情况,表示物体是输入了能量还是输出了能量。
[例1] 如图1所示,质量为m的物体静止于倾角为 ,质量为M的斜面体上,现对该斜面体施一水平向左的推力F,使物体随斜面体一起沿水平方向向左匀速运动,位移为s,求在此过程中物体所受重力、支持力、摩擦力各对物体做了多少功?
,质量为M的斜面体上,现对该斜面体施一水平向左的推力F,使物体随斜面体一起沿水平方向向左匀速运动,位移为s,求在此过程中物体所受重力、支持力、摩擦力各对物体做了多少功?

图1
析与解:物体的受力情况如图2所示,由于物体处于匀速运动状态,可由共点力的平衡条件得,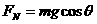 ,
, ,且
,且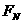 与s间的夹角为
与s间的夹角为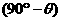 ,
,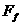 与s间的夹角为
与s间的夹角为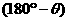 ,所以:
,所以: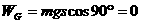


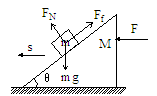
图2
说明:若力和位移不在一条直线,求力对物体做功时,可将力正交分解,使其一个分力与位移在一条直线上,另一个分力与位移垂直,也可以将位移按类似的方法正交分解。
3. 做功快慢的描述问题
做功的快慢程度用功率来描述,功率的定义式是: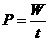
功率的导出式是: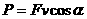
前者用于计算某段时间内的平均功率,后者则用于计算某个时刻瞬时功率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com