
题目列表(包括答案和解析)
高中阶段,万有引力定律主要应用于分析天体运动和人造卫星问题。处理此类问题的基本方法:(1)将天体运动和人造卫星的运动近似看成匀速圆周运动,其所需向心力由万有引力提供,即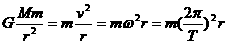 ,应用时根据实际情况选择不同的关系式。(2)物体在任何天体表面受到的重力近似等于万有引力,即
,应用时根据实际情况选择不同的关系式。(2)物体在任何天体表面受到的重力近似等于万有引力,即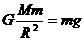 ,其中R是天体半径。在实际应用中,形形色色的问题又可以演化为下面三个模型。
,其中R是天体半径。在实际应用中,形形色色的问题又可以演化为下面三个模型。
1. “点”绕“点”的问题。
此类问题中做圆周运动的天体及提供向心力的天体,当两者间距远大于各自形体大小时,均视为质点。
有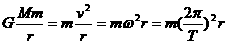
此时轨道半径r等于两天体间距离。
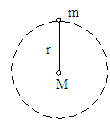
例1:已知地球绕太阳的公转轨道半径为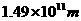 ,公转周期为
,公转周期为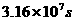 ,万有引力恒量
,万有引力恒量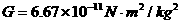 。试估算太阳的质量是多少?
。试估算太阳的质量是多少?
解析:设太阳质量为M,地球质量为m,地球到太阳的距离为r,公转周期为T。
由万有引力提供向心力,对地球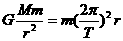
解得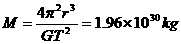
6. 加速度问题
经天文学家观察,太阳在绕着银河系中心圆形轨道上运行,轨道半径约为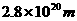 ,转动一周的时间约为
,转动一周的时间约为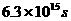 。太阳做圆周运动的向心力是来自它轨道内侧的大量星体的引力,可以把这些星体的全部质量看作集中在银河系中心来处理问题。求:(1)从给出的数据来计算太阳轨道内侧这些星体的总质量M。(2)太阳在圆周运动轨道上的加速度a。
。太阳做圆周运动的向心力是来自它轨道内侧的大量星体的引力,可以把这些星体的全部质量看作集中在银河系中心来处理问题。求:(1)从给出的数据来计算太阳轨道内侧这些星体的总质量M。(2)太阳在圆周运动轨道上的加速度a。
解析:
(1)设太阳质量为m,轨道半径为R,周期为T,由牛顿第二定律有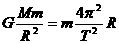
所以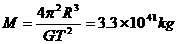
(2)太阳在圆周运动轨道上的加速度就是太阳的向心加速度,所以有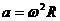
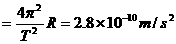 。
。
通过以上分析可见,这五种题型表面上看各不相同,每种类型都是一个独立的个体,但在解法上都用了牛顿第二定律知识,即万有引力提供向心力,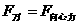 。
。
5. 速度问题
俄罗斯“和平号”空间站在人类航天史上写下了辉煌的篇章,因不能保障其继续运行,于2001年3月20号坠入太平洋,坠落时地面指挥系统使空间站在极短的时间内向前喷出部分高速气体,使其速度瞬间变小,在万有引力的作用下坠落。设该空间站在离地面高度为h的轨道上绕地球做匀速圆周运动,地球表面的重力加速度为g,地球半径为R。求该空间站做圆周运动时的速度?
解析:空间站绕地球做匀速圆周运动,万有引力提供向心力,根据万有引力定律和牛顿第二定律有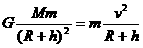 ①
①
又在地面表面附近质量为 物体有
物体有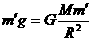 ②
②
①②联立解得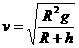
4. 密度问题
中子星是恒星演化过程中一种可能结果,它的密度很大。现有一中子星,观察到它的自转周期为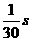 。问该中子星的最小密度应为多少才能维持该星体的稳定,不致因自转而瓦解。计算时星体可视为均匀球体。(引力常数
。问该中子星的最小密度应为多少才能维持该星体的稳定,不致因自转而瓦解。计算时星体可视为均匀球体。(引力常数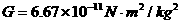 )
)
解析:考虑中子星赤道一小块物质,只有当它受到的万有引力大于或等于它随星体一起旋转所需的向心力时,中子星才不会瓦解。设中子星的密度为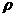 ,质量为M,半径为r,周期为T,位于赤道处的小块物质质量为m,则有
,质量为M,半径为r,周期为T,位于赤道处的小块物质质量为m,则有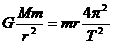 ,又因为
,又因为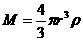 ,由以上各式解得
,由以上各式解得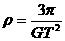
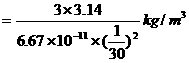
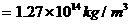
3. 质量问题
为了研究太阳演化进程,需知道目前太阳的质量M,已知地球半径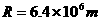 ,地球质量
,地球质量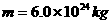 ,日地中心的距离
,日地中心的距离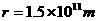 ,地球表面处的重力加速度
,地球表面处的重力加速度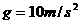 ,1年约为
,1年约为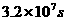 ,试估算目前太阳的质量M。
,试估算目前太阳的质量M。
解析:地球绕太阳做圆周运动,万有引力提供向心力,根据万有引力定律和牛顿第二定律有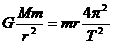 ①
①
对地球表面处质量为 物体有
物体有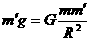 ②
②
①②联立解得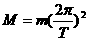
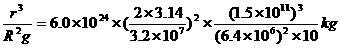
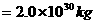
2. 周期问题
组成星球的物质是靠引力吸引在一起的,这样的星球有一个最大的自转速率,如果超过了该速率,星球的万有引力将不足以维持其赤道附近的物体做圆周运动,由此能得到半径为r,密度为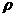 ,质量为M且均匀分布的星球的最小自转周期T,下列表达式中正确的是:
,质量为M且均匀分布的星球的最小自转周期T,下列表达式中正确的是:
A. 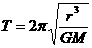 B.
B. 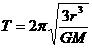 C.
C. 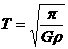 D.
D. 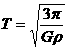
解析:万有引力提供向心力,根据万有引力定律和牛顿第二定律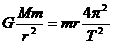
解得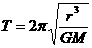
又质量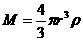 ,代入上式得
,代入上式得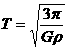
所以正确选项为A、D
1. 距离问题
已知地球半径约为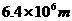 ,又知月球绕地球的运动可近似看作匀速圆周运动,则可估算出月球到地心的距离约为 m。(结果保留一位有效数字)
,又知月球绕地球的运动可近似看作匀速圆周运动,则可估算出月球到地心的距离约为 m。(结果保留一位有效数字)
解:月球绕地球运转一周的时间约为30天,合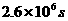 。万有引力提供向心力,根据万有引力定律和牛顿第二定律
。万有引力提供向心力,根据万有引力定律和牛顿第二定律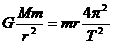 ①
①
对地球上质量为 的物体有
的物体有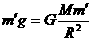 ②
②
①②联立解得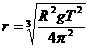
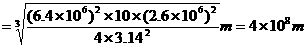
8. 宇宙飞船上的科研人员在探索某星球时,完成了下面两个实验:① 当飞船停留在距该星球一定的距离时,正对着该星球发出一个激光脉冲,经时间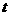 后收到反射回来的信号,此时该星球直径与观察者的眼睛所对的角度为
后收到反射回来的信号,此时该星球直径与观察者的眼睛所对的角度为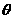 (如图2所示)。② 当飞船在该星球着陆后,科研人员在距星球表面
(如图2所示)。② 当飞船在该星球着陆后,科研人员在距星球表面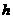 高处以初速度
高处以初速度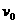 水平抛出一小球,测出落地点到抛出点的水平距离为
水平抛出一小球,测出落地点到抛出点的水平距离为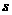 。
。
又已知万有引力常量为G,光速为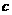 ,星球的自转以及大气对物体的阻力均可不计。试根据以上信息,求:
,星球的自转以及大气对物体的阻力均可不计。试根据以上信息,求:
(1)星球的半径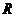 ;
;
(2)星球的质量M;
(3)星球的第一宇宙速度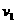 。
。
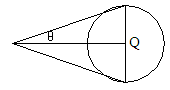
图2
7. 当两个物体不能视作质点时,两物体之间的万有引力不能用公式直接计算,但可以用下述方法计算:将两个物体各分成很多质点,一个物体的每个质点与另外一个物体的每个质点之间都存在万有引力,这些质点之间的万有引力可用公式计算,所有质点间万有引力的合力就是这两个物体间的万有引力,现设想把一个质量为 的小球(可看作质点)放到地球的中心,则此小球与地球之间的万有引力为 (已知地球质量M,半径为R)。
的小球(可看作质点)放到地球的中心,则此小球与地球之间的万有引力为 (已知地球质量M,半径为R)。
6. 如图1所示,有A、B两颗行星绕同一恒星O做圆周运动,旋转方向相同,A行星的周期为T1,B行星的周期为T2,在某一时刻两行星第一次相遇(即两颗行星相距最近),则经过时间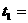 时两行星第二次相遇,经过时间
时两行星第二次相遇,经过时间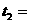 时两行星第一次相距最远。
时两行星第一次相距最远。
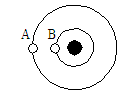
图1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com