
题目列表(包括答案和解析)
1.C 2.B 3.B 4.A 5.C 6.C 7.B 8.D 9.D 10.C 11.B 12.D 13.B 14.C 15.C 16.C 17.C 18.C 19.C 20.D 21.D 22.D 23.D 24.B 25.C 26.C 27.A 28.D 239.C 30.B 31.C 32.B 33.A 34.C 35.B 36.A 37.D 38.C 39.B 40.C 41.B 42.C 43.A 44.B 45.C 46.C 47.A 48.B
31. (2008新疆乌鲁木齐市)宝宝和贝贝是一对双胞胎,他们参加奥运志愿者选拔并与甲、乙、丙三人都进入了前5名.现从这5名入选者中确定2名作为志愿者.试用画树形图或列表的方法求出:
(1)宝宝和贝贝同时入选的概率;
(2)宝宝和贝贝至少有一人入选的概率.
概率答案
30. (2008宁夏)张红和王伟为了争取到一张观看奥运知识竞赛的入场券,他们各自设计了一个方案:
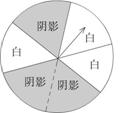
张红的方案是:转动如图所示的转盘,如果指针停在阴影区域,则张红得到入场券;如果指针停在白色区域,则王伟得到入场券(转盘被等分成6个扇形.若指针停在边界处,则重新转动转盘).
王伟的方案是:从一副扑克牌中取出方块1、2、3,将它们背面朝上重新洗牌后,从中摸出一张,记录下牌面数字后放回,洗匀后再摸出一张.若摸出两张牌面数字之和为奇数,则张红得到入场劵;若摸出两张牌面数字之和为偶数,则王伟得到入场券.
(1)计算张红获得入场券的概率,并说明张红的方案是否公平?
(2)用树状图(或列表法)列举王伟设计方案的所有情况,
计算王伟获得入场券的概率,并说明王伟的方案是否公平?
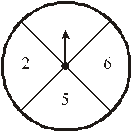
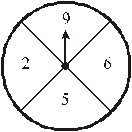
29.(2008云南省)如图,一个被等分成4个扇形的圆形转盘,其中3个扇形分别标有数字2,5,6,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动转盘).
(1)求当转动这个转盘,转盘自由停止后,指针指向没有标数字的扇形的概率;
(2)请在4,7,8,9这4个数字中选出一个数字填写在没有标数字的扇形内,使得分别转动转盘2次,转盘自由停止后指针所指扇形的数字和分别为奇数与为偶数的概率相等,并说明理由.
28.(2008年四川省南充市)桌面上放有质地均匀、反面相同的3张卡片,正面分别标有数字1,2,3,这些卡片反面朝上洗匀后放在桌面上,甲从中任意抽出1张,记下卡片上的数字后仍反面朝上放回洗匀,乙再从中任意抽出1张,记下卡片上的数字,然后将这两数相加.
(1)请用列表或画树形图的方法求两数和为4的概率;
(2)若甲与乙按上述方式做游戏,当两数之和为4时,甲胜,反之则乙胜;若甲胜一次得6分,那么乙胜一次得多少分,这个游戏才对双方公平?
27.(2008年湖南省邵阳市)已知分式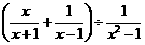 ,及一组数据:
,及一组数据: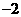 ,
,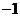 ,1,2.
,1,2.
(1)从已知数据中随机选取一个数代替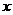 ,能使已知分式有意义的概率是多少?
,能使已知分式有意义的概率是多少?
(2)先将已知分式化简,再从已知数据中选取一个你喜欢的,且使已知分式有意义的数代替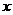 求值.
求值.
26.(2008福建省泉州市)小王制定一个玩飞行棋的游戏规则为:抛掷两枚均匀的正四面体骰子(四面依次标上数字1、2、3、4)掷得点数p之为5时才“可以起飞 ”,请你根据规则计算“可以起飞”的概率。(要求用树状图或列表法求解。
25.(2008年山东省青岛市)实际问题:某学校共有18个教学班,每班的学生数都是40人.为了解学生课余时间上网情况,学校打算做一次抽样调查,如果要确保全校抽取出来的学生中至少有10人在同一班级,那么全校最少需抽取多少名学生?
建立模型:为解决上面的“实际问题”,我们先建立并研究下面从口袋中摸球的数学模型:
在不透明的口袋中装有红、黄、白三种颜色的小球各20个(除颜色外完全相同),现要确保从口袋中随机摸出的小球至少有10个是同色的,则最少需摸出多少个小球?
为了找到解决问题的办法,我们可把上述问题简单化:
(1)我们首先考虑最简单的情况:即要确保从口袋中摸出的小球至少有2个是同色的,则最少需摸出多少个小球?
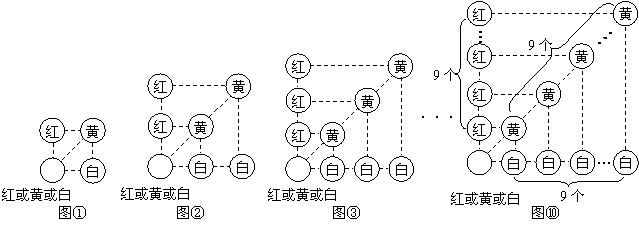
假若从袋中随机摸出3个小球,它们的颜色可能会出现多种情况,其中最不利的情况就是它们的颜色各不相同,那么只需再从袋中摸出1个小球就可确保至少有2个小球同色,即最少需摸出小球的个数是:1+3=4(如图①);
(2)若要确保从口袋中摸出的小球至少有3个是同色的呢?
我们只需在(1)的基础上,再从袋中摸出3个小球,就可确保至少有3个小球同色,即最少需摸出小球的个数是:1+3×2=7(如图②)
(3)若要确保从口袋中摸出的小球至少有4个是同色的呢?
我们只需在(2)的基础上,再从袋中摸出3个小球,就可确保至少有4个小球同色,即最少需摸出小球的个数是:1+3×3=10(如图③):

(10)若要确保从口袋中摸出的小球至少有10个是同色的呢?
我们只需在(9)的基础上,再从袋中摸出3个小球,就可确保至少有10个小球同色,即最少需摸出小球的个数是:1+3×(10-1)=28(如图⑩)

模型拓展一:在不透明的口袋中装有红、黄、白、蓝、绿五种颜色的小球各20个(除颜色外完全相同),现从袋中随机摸球:
(1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是 ;
(2)若要确保摸出的小球至少有10个同色,则最少需摸出小球的个数是 ;
(3)若要确保摸出的小球至少有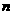 个同色(
个同色(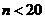 ),则最少需摸出小球的个数是 .
),则最少需摸出小球的个数是 .
模型拓展二:在不透明口袋中装有 种颜色的小球各20个(除颜色外完全相同),现从袋中随机摸球:
种颜色的小球各20个(除颜色外完全相同),现从袋中随机摸球:
(1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是 .
(2)若要确保摸出的小球至少有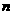 个同色(
个同色(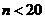 ),则最少需摸出小球的个数是 .
),则最少需摸出小球的个数是 .
问题解决:(1)请把本题中的“实际问题”转化为一个从口袋中摸球的数学模型;
(2)根据(1)中建立的数学模型,求出全校最少需抽取多少名学生.
24.(2008年吉林省长春市)汉字是世界上最古老的文字之一,字形结
构体现人类追求均衡对称、和谐稳定的天性.如图,三个汉字可以看成是轴对称图形.

(1)请在方框中再写出2个类似轴对称图形的汉字;
(2)小敏和小慧利用“土”、“口”、“木”三个汉字设计一个游戏,规则如下:将这三个汉字分别写在背面都相同的三张卡片上,背面朝上洗匀后抽出一张,放回洗匀后再抽出一张,若两次抽出的汉字能构成上下结构的汉字(如“土”“土”构成“圭”)小敏获胜,否则小慧获胜.你认为这个游戏对谁有利?请用列表或画树状图的方法进行分析并写出构成的汉字进行说明.
23.(2008年江苏省连云港市)甲、乙两人玩“锤子、石头、剪子、布”游戏,他们在不透明的袋子中放入形状、大小均相同的15张卡片,其中写有“锤子”、“石头”、“剪子”、“布”的卡片张数分别为2,3,4,6.两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“锤子”胜“石头”和“剪子”,“石头”胜“剪子”,“剪子”胜“布”,“布”胜“锤子”和“石头”,同种卡片不分胜负.
(1)若甲先摸,则他摸出“石头”的概率是多少?
(2)若甲先摸出了“石头”,则乙获胜的概率是多少?
(3)若甲先摸,则他先摸出哪种卡片获胜的可能性最大?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com