4．今年5月1日是星期三，你能否推算出今年10月1日是星期几？

3．运用加、减、乘、除四种运算，如何由四个数2，7，10，4(每个数只能用一次)得到24，你能想出几个算式？写出来。

2．银行计算利息是存入的钱数(本金)与存入的时间数(期数)及每期的利率的积。某人将1万元按一年定期储蓄存入银行，月利率是1.88‰(读作千分之一点八八)，到期后交利息税20%，问此人最后可得利息为多少元？

1．小华买了60分和80分的邮票共10枚，花了7元2角，那么60分和80分的邮票各买了几枚？

5．观察前两个三角形里的各四个数，按此规律在第三个三角形的“？”处填上适当的数．

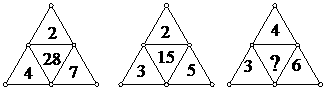
这一章我们一起初步接触了一些数学，并且也初步尝试了简单地“做数学”．数学是动脑筋的学科，要想学好数学，就要多想，多做，还要认真读书，认真听老师的讲解，也要多和同学讨论，多向老师请教．才能学好数学．

4．观察前两个方框里的各四个数，找出规律，在后两个方框中的“？”处填上适当的数．

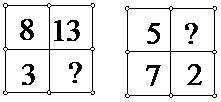
3．有一堆桃子，第一只猴子拿走一半加半个，第二只猴子又拿走剩下的一半加半个，第三、第四、第五只猴子依照这种方式拿走桃子，最后还剩下一只桃子．原来这堆桃子共有多少只？

2．有一堆棋子，把它四等分后剩一枚，取走三份和这一枚；剩下的再四等分又剩一枚，再取走三份和这一枚；剩下的再四等分又剩一枚，原来至少有多少枚棋子？

1．找规律，在(　 )内填上适当的数：

(1)1，3，6，10，(　　　　 )，21，(　　　　　　　 )，(　　　　　　　 )；

(2)1，3，7，15，(　　　　 )；63，(　　　　　　　 )；

(3)，，(　　　　 )，，；

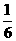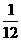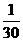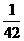(4)，，，，(　　　　　　　 )；

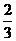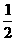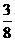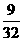(5)，，，(　 )，，(　　　　　　 )， ．

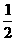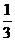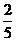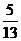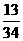4．高斯小时候能够很快地算出：1+2+3+……+99+100=5050，想必同学们都知道他是如何思考和计算的，你能计算2+4+6+……+98+100吗？你能用几种方法算这个题？

§1.2让我们来做数学

我国著名数学家苏步青先生曾说过：学数学的最好方法，就是做数学．当然，“做数学”先要从做数学习题开始．同学们先学着做一些数学习题，通过正确地解答数学习题，学会和掌握解决数学问题的方法．

例1 找规律，在(　　　 )内填上适当的数：

(1)2，4，8，16，(　　　　 )；

(2)1，4，9，16，(　　　　 )；

(3)，，，，(　　　　 )．

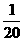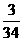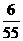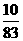解：(1)由前四个数看出，从第二个数起，后一个数是前面一个数的2倍，括号内应填32；

(2)前四个数正好是1，2，3，4的平方，故括号内应填5的平方25；本题也可以这样看，第二个数是第一个数加3，第三个数是第二个数加5，第四个数是第三个数加7，那么该填的数应是第四个数加9为25；

(3)我们分别看分子和分母，第二个分子是第一个分子加2，第三个分子是第二个分子加3，第四个分子是第三个分子加4，那么该填的分子应是第四个分子加5为15；第二个分母是第一个分母加14即2×7，第三个分母是第二个分母加21即3×7，第四个分母是第三个分母加28即4×7，那么该填的分母应是第四个分母加5×7为118；故括号内应填分数为．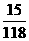

说明：找规律是解决数学问题的一个重要方法，找规律时要整体地看问题，才能准确、快速地找出规律，上述问题都是比较简单的，以后我们还会学习较为复杂的找规律的问题．

例2 李明从图书馆借来一批书给同学们看，先给了甲5本和剩下的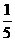；又给了乙4本和剩下的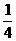；然后又给了丙3本和剩下的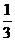；再给了丁2本和剩下的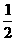，最后还剩下2本．求李明从图书馆共借来多少本书．

分析 由于每次给一个人的书数都不能确定多少，而和剩下的书数有关，我们可以从最后剩下的两本书开始向前推算．

解 在给了丁2本书和剩下的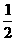后，还剩两本书，也就是说给丁剩下的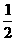是2本书，即给丁书之前，还有6本书，这6本书是给丙3本书后剩下的书的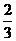，即给丙书之前，还剩12本书，这12本书又是给乙4本书后剩下的书的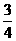，即给乙书之前，应有20本书，这20本书是给甲5本书之后剩下的书的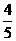，即甲拿到5本书之后还剩25本书，即李明从图书馆共借来30本书．

说明 当正面解决问题不很方便时，可采用这种逆推法．

例3 计算1+3，1+3+5，1+3+5+7，找出规律，猜测1+3+5+7+……+99的结果．

解1+3=4=2²，1+3+5=9=3²，1+3+5+7=16=4²，这三个算式都是从1开始的连续奇数的和，它们的结果都等于连续奇数的个数的平方，而

1+3+5+7+……+99是从1开始的50个连续奇数的和，于是

1+3+5+7+……+99=50²=2500．

说明 学习数学要学会合理的猜测，猜测是基于认真地观察，找出条件给出的规律，作出猜测．学习数学还要有严格的推理，以说明猜测的正确性．这个例题只给出了猜测的结果，我们以后还要学会推理．这也是中学数学比小学数学更深一层的地方．

习题1.2