
题目列表(包括答案和解析)
1.课本第42页习题8.1的第1、2题。
课后练习:
(1)x是负数;_________________ (2)x是非负数;________________
(3)x的一半小于-1。_______________ (4)x与4的和大于0.5。____________
例2、x=2是不等式x-1<2的解吗?x=3?x=4?(格式)
例3列不等式: (1)一个数的绝对值不小于0。________
(2)两数积的2倍不大于这两数的平方和。_________。
问题1:我们只用120元买了30张票,我们是不是就买30张票?请大家讨论。 _______________________-
问题2:买30张票比买27张票付的款还要少,这是不是说多买票反而花钱少?如果你一个人去参观,是不是也买30张呢?
请你计算10人、20人、21人、22人、23人、24人、25人、26人……去的时候,分别要付多少钱?
|
人数 |
10 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
|
所付钱数 |
|
|
|
|
|
|
|
|
|
问题3:至少要有多少人去参观,多买票反而便宜?能否用数学知识来解决?
引导学生分析。 设有x人要去公园参观。
(1)如果x≥30,则按实际人数买票,每张票只要付_______元。
(2)如果x<30,那么:按实际人数买票x张,要付款______元;买30张票要付款4×30=120元。
如果买30张票合算,则120<5x。
问题4:x取哪些数值时,上式成立?
(1)你能否结合前面学的解方程的知识,尝试解这个不等式。
(2)列表计算。
|
X |
5X |
比较120与5X的大小 |
120< 5X成立吗? |
|
21 |
|
|
|
|
22 |
|
|
|
|
23 |
|
|
|
|
24 |
|
|
|
|
25 |
|
|
|
|
26 |
|
|
|
|
27 |
… |
… |
… |
|
28 |
|
|
|
|
29 |
|
|
|
|
30 |
|
|
|
问题5:由上表可知,当x=______________时,也就是说,至少要有25人进公园时,买30张合算。即当x>24时,5x,120。
例1 用不等式表示:
(1)x是负数;_________________ (2)x是非负数;________________
(3)x的一半小于-1。_______________ (4)x与4的和大于0.5。____________
2.概括总结。
(1)像上面出现的135>120,27<30,5x>20,x<30那样用不等号“<”或“>”表示不等关系的式子,叫做不等式。
不等号有:<、>、≠、≤、≥。
(2)不等式120<5x中含有未知x。能使不等式成立的未知数的值,叫做不等式的解。
不等式的解可以有无数个。
如上例中,x=25,26,27,…等都是120<5x的解,x=24,23,22,21则都不是不等式的解。
公园(或本地区的某个旅游景点)的票价是每人5元。团体参观旅游优惠,一次购票满30张,每张票可少收1元。某班有27名学生去公园进行参观活动,假如要你去买票,请问你打算买多少张?
1)买27张票,要付款:_______元。
2)买30张票,要付款:________元。
27张<30张,135元>120元。
3)引导学生:你说是买30张票花钱少还是买27张票花钱少?
2、学校将若干间宿舍分配给七年级一班的女生住宿,已知该班女生少于35人,若每个房间住5人,则剩下5人没处住;若每个房间住8人,则空一间房,并且还有一间房也不满。有多少间宿舍,多少名女生?
1、若方程组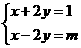 的解
的解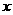 、
、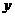 的值都不大于1,求
的值都不大于1,求 的取值范围。
的取值范围。
2、小华家距离学校2.4千米.某一天小华从家中去上学恰好行走到一半的路程时,发现离到校时间只有12分钟了.如果小华能按时赶到学校,那么他行走剩下的一半路程的平均速度至少要达到多少?
解:设 ,依题意得:
1、某次知识竞赛共有20道选择题.对于每一道题,若答对了,则得10分;若答错了或不答,则扣3分.请问至少要答对几道题,总得分才不少于70分?
解:设 ,依题意得:
(1)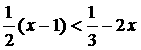 (2)
(2)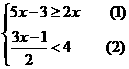
(3)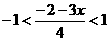 (4)
(4)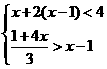
5、已知不等式组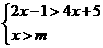 无解,则
无解,则 的取值范围是
的取值范围是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com