8．计算：7.6×199.8+4.3×199.8-1.9×199.8．

7．如果x²-ax+5有一个因式是(x+1)，求a的值，并求另一个因式．

6．如果2x²+mx-2可因式分解为(2x+1)(x-2)，那么m的值是(　 )

　 　A．-1　　 B．1　　　 C．-3　　　 D．3

5．把下列各式分解因式：

(1)y²-16；　　　　　　　　　　　　 (2)25m²-n²；

(3)x²+14x+49；　　　　　　　　　　 (4)4-4x+x²．

提高训练　　　　　　　　　　　　　　　　　　　　　　　　　

4．在下列各式中等号右边的括号前填入适当的单项式或正负号，使等式左右两边相等．

　　 (1)-a+b=______(a-b)；　　　　 (2)-2x-2y=_______(x+y)；

　　 (3)(a+b)(a-b)=______(a+b)(a-b)；(4)(a-b)²=______(b-a)²；

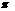　　 (5)2R-2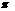r=______(R-r)；　 (6)-8a²b-2ab+6b²=________(4a²+a-3b)．

3．下列各式因式分解错误的是(　 )

　　 A．8x²y-24xy²=8xy(x-3y);　　 　　　　　B．ax+bx+ay+by=x(a+b)+y(a+b)

　　 C．12x²y+14x²y²-2xy=2xy(6x+7xy-1);　　 D．x³-8=(x-2)(x²+2x+4)

2．下列各式从左到右的变形中，是因式分解的是(　 )

　　 A．(a+3)(a-3)=a²-9;　　 B．a³+b³=(a+b)(a²-ab+b²)

　　 C．a²-4a-5=(a-2)²-9;　 　D．a²-4a-5=a(a-4)-5

1．下列由左到右的变形哪些是因式分解，哪些不是(是的打“∨”，不是的打“×”)：

　　 (1)(x+3)(x-3)=x²-9； (　 );　 (2)x²+2x+2=(x+1)²+1；(　 )

　　 (3)x²-x-12=(x+3)(x-4)；(　 );　 (4)x²+3xy+2y²=(x+2y)(x+y)；(　 )

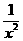　　 (5)1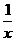-=(1+)(1-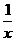)；(　 );(6)m²+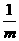+2=(m+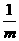)²；(　 )

　　 (7)a³-b³=(a-b)(a²+ab+b²)．(　 )

3．因式分解的结果必须是几个整式的积的形式，而不是几个整式的积与某项的和差形式．

范例积累　　　　　　　　　　　　　　　　　　　　　　　　　 　

　　 [例1]　 判断下列各式从左到右的变形是否是因式分解，用“∨”表示是，用“×”表示不是．

　　 (1)(a+b)(a-b)=a²-b²；(　 )　　 (2)3x³-6x²-3x=3x(x²-2x-1)；(　 )

　　 (3)m³-m²-m=m(m²-m)；(　 )　　　 (4)x²+2x-3=x(x+2)-3．(　 )

　　 [分析]　 应用因式分解的定义和整式乘法的计算进行判断．

　　 [解]　 (1)×．本题是整式乘法运算．

　　 (2)∨．本题是把多项式化成乘积形式，用单项式乘以多项式法则计算等式右边结果与左边相等，所以是因式分解．

　　 (3)×．经计算等式不成立．

　　 (4)×．等式右边不是因式乘积形式．

　　 [注意]　 运用定义进行判断、计算是解题的最常见的方法．要注意因式分解是恒等变形，是整式乘法的相反形式??砸?榛畹卦擞贸朔ǚ峙渎桑？

　　 [例2]　 下列各因式分解正确的是(　 )

　　 　A．x²y+y-3xy=y(x²-3x);　　　　 　　B．-a²-ab+ac=-a(a-b+c)

　　 　C．12x²y+14x²y²-2xy=2xy(6x+7xy-1);D．a²-4+3a=(a+1)(a-4)

　　 [分析]　 由于因式分解与整式乘法是互逆变形，利用这种关系，我们可以从整式乘法来判断因式分解的结果．

　　 [解]　 A、B、D通过整式乘法计算后，等式左右两边都不相等，C等式左右两边相等，故选C．

　　 [例3]　 (1)当a=102，b=98时，求a²-b²的值；

　　 (2)计算：2004²-2004×2003．

　　 [解]　 (1)因为a²-b²=(a+b)(a-b)，把a=102，b=98代入上式得a²-b²=(a+b)(a-b)=(102+98)(102-98)=200×4=800；

　　 (2)2004²-2004×2003=2004×(2004-2003)=2004×1=2004．

　　 [注意]　 在解题过程中，通过因式分解，有时可使计算简便．

基础训练

2．因式分解是多项式的一种变形，就是把多项式转化为乘积的形式，它与整式乘法正好是相反的变形．