
题目列表(包括答案和解析)
20.7 反比例函数的图象、性质和应用练习
第1题. 如果正比例函数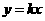 与反比例函数
与反比例函数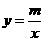 图象的一个交点为
图象的一个交点为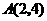 ,那么
,那么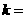 ,
,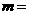 .
.
答案:2,8
第2题. 已知点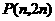 是第一象限的点,下面四个命题:
是第一象限的点,下面四个命题:
①点 关于
关于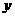 轴对称的点
轴对称的点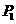 的坐标是
的坐标是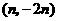 ②点
②点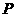 到原点
到原点 的距离是
的距离是 ③直线
③直线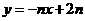 不经过第三象限④对于函数
不经过第三象限④对于函数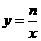 ,当
,当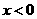 时,
时,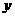 随
随 的增大而减小
的增大而减小
其中命题不正确的是 (填上所有命题的序号).
答案:①②
第3题. 已知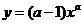 是反比例函数,则它的图象在( )
是反比例函数,则它的图象在( )
A.第一,三象限 B.第二,四象限
C.第一,二象限 D.第三,四象限
答案:B
第4题. 若点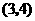 是反比例函数
是反比例函数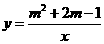 图象上一点,则函数图象必经过点( )
图象上一点,则函数图象必经过点( )
A.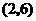 B.
B.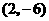 C.
C.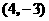 D.
D.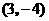
答案:A
第5题. 如图,一次函数的图象与 轴,
轴,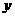 轴分别交于
轴分别交于 ,
,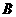 两点,与反比例函数的图象交于
两点,与反比例函数的图象交于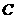 ,
,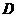 两点.如果
两点.如果 点的坐标为
点的坐标为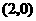 ,点
,点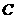 ,
,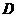 分别在第一,三象限,且
分别在第一,三象限,且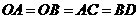 .试求一次函数和反比例函数的解析式.
.试求一次函数和反比例函数的解析式.
答案:设一次函数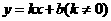 ,由
,由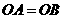 ,
,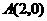
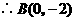 ,而
,而 ,
,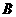 在一次函数图象上,
在一次函数图象上,
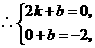 解得
解得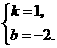
 一次函数解析式为
一次函数解析式为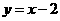 .
.
过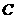 点作
点作 垂直于
垂直于 轴,垂足为
轴,垂足为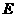 .
.
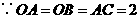 ,
,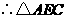 为等腰直角三角形.
为等腰直角三角形.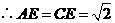 .
.
点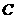 的坐标为
的坐标为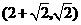
设反比例函数解析式为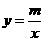 ,
,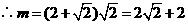 .
.
故反比例函数解析式为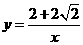 .
.
第6题. 如图,已知点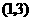 在函数
在函数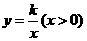 的图象上,矩形
的图象上,矩形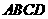 的边
的边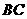 在
在 轴上,
轴上,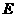 是对角线
是对角线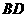 的中点.函数
的中点.函数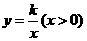 的图象经过
的图象经过 ,
,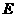 两点,点
两点,点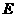 的横坐标为
的横坐标为 .
.
(1)求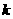 的值;
的值;
(2)求点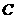 的横坐标(用
的横坐标(用 表示);
表示);
(3)当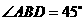 ,求
,求 的值.
的值.
答案:(1)把点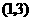 代入
代入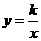 中,求出
中,求出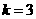 .
.
(2)当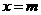 时,
时,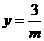 ,当
,当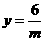 时,
时,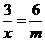 ,
,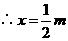 ,即
,即 点横坐标为
点横坐标为 ,那么
,那么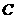 点横坐标为
点横坐标为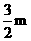 .
.
(3)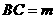 ,当
,当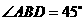 时,
时,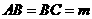 ,
, 点坐标为
点坐标为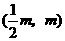 代入
代入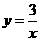 中,得
中,得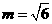 .
.
第7题. 如图,已知一次函数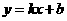 的图象与反比例函数
的图象与反比例函数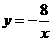 的图象交于
的图象交于 ,
,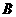 两点,且点
两点,且点 的横坐标和
的横坐标和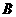 点的纵坐标都是
点的纵坐标都是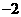 .求:
.求:
 (1)一次函数解析式;
(1)一次函数解析式;
(2)求 的面积.
的面积.
答案:(1)先求 点坐标为
点坐标为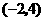 ,
,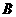 点坐标为
点坐标为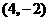 ,
,
把 ,
,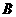 两点坐标代入
两点坐标代入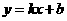 中,得
中,得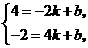
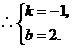
 一次函数解析式为
一次函数解析式为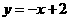 .
.
(2)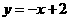 与
与 轴交点坐标
轴交点坐标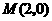 ,即
,即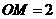 ,
,
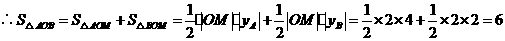
第8题. 已知反比例函数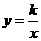 的图象经过点
的图象经过点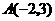 .
.
(1)求反比例函数的解析式;
(2)经过点 的正比例函数
的正比例函数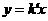 的图象与反比例函数
的图象与反比例函数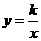 的图象还有其他交点吗?若有,求出交点坐标;若没有,请说明理由.
的图象还有其他交点吗?若有,求出交点坐标;若没有,请说明理由.
答案:(1)把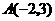 代入
代入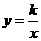 中,求出
中,求出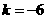 ,
, 反比例函数解析式为
反比例函数解析式为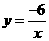 .
.
(2)有. 正,反比例函数的图象关于原点对称,且点
正,反比例函数的图象关于原点对称,且点 在它们的图象上,
在它们的图象上,
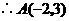 关于原点的对称点
关于原点的对称点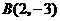 也在它们的图象上,它们相交的另一个交点坐标为
也在它们的图象上,它们相交的另一个交点坐标为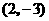 .
.
第9题. 如图,过反比例函数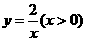 的图象上任意两点
的图象上任意两点 ,
, 分别作
分别作 轴的垂线,垂足为
轴的垂线,垂足为 ,
, ,连接
,连接 ,
,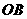 ,设
,设 与
与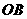 的交点为
的交点为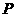 ,
, 与梯形
与梯形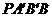 的面积分别为
的面积分别为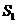 ,
,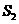 ,比较它们的大小,可有( )
,比较它们的大小,可有( )
 A.
A.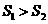 B.
B.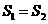 C.
C.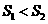 D.大小关系不能确定
D.大小关系不能确定
答案:B
第10题. 已知函数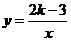 ,当
,当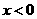 时,
时,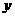 随
随 的增大而减小,那么
的增大而减小,那么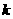 的取值范围是 .
的取值范围是 .
答案: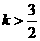
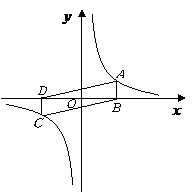
第11题. 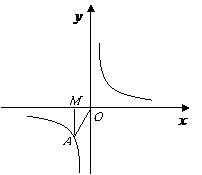 一个反比例函数在第三象限的图象如图所示,若
一个反比例函数在第三象限的图象如图所示,若 是图象上任意一点,
是图象上任意一点,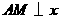 轴于
轴于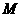 ,
, 是原点,如果
是原点,如果 的面积是3,那么这个反比例函数的解析式是 .
的面积是3,那么这个反比例函数的解析式是 .
答案: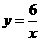
第12题. 若点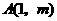 在函数
在函数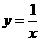 的图象上,则点
的图象上,则点 关于
关于 轴的对称点坐标是 .
轴的对称点坐标是 .
答案: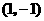
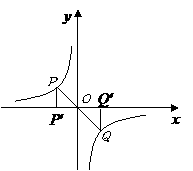
第13题. 如图,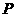 ,
,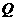 为反比例函数
为反比例函数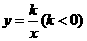 的图象上任意两点,
的图象上任意两点,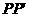 ,
, 分别垂直
分别垂直 轴于
轴于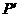 ,
,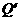 ,则
,则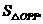 与
与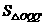 面积的大小关系是 .
面积的大小关系是 .
答案: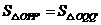
第14题. 如图,函数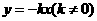 与
与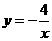 的图象交于
的图象交于 ,
, 两点,过
两点,过 点作
点作 垂直于
垂直于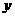 轴,垂足为点
轴,垂足为点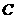 ,则
,则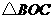 的面积为 .
的面积为 .
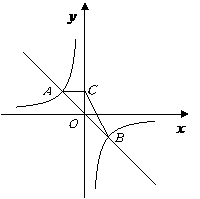
答案:2
第15题. 如图,点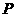 是
是 轴正半轴上的一个动点,过点
轴正半轴上的一个动点,过点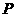 作
作 轴的垂线,交双曲线
轴的垂线,交双曲线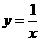 于点
于点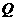 ,连结
,连结 ,当点
,当点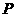 沿
沿 轴的正方向运动时,
轴的正方向运动时, 的面积( )
的面积( )
A.逐渐增大 B.逐渐减小 C.保持不变 D.无法确定
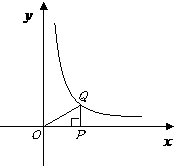
答案:C
第16题. 若点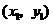 ,
,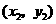 ,
,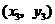 都是
都是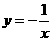 的图象上的点,且
的图象上的点,且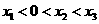 ,则下列各式中正确的是( )
,则下列各式中正确的是( )
A.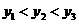 B.
B.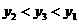 C.
C.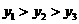 D.
D.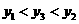
答案:B
第17题. 如图, ,
,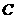 是函数
是函数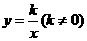 的图象上关于原点对称的任意两点,
的图象上关于原点对称的任意两点,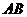 ,
,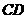 垂直于
垂直于 轴,垂足分别为
轴,垂足分别为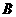 ,
,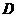 ,那么四边形
,那么四边形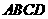 的面积
的面积 是( )
是( )
 A.
A.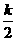 B.
B.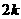 C.
C.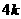 D.
D.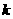
答案:B
第18题. 已知反比例函数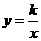 和一次函数
和一次函数 的图象的一个交点是
的图象的一个交点是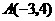 ,且一次函数的图象与
,且一次函数的图象与 轴的交点到原点的距离为5,分别确定反比例函数和一次函数的解析式.
轴的交点到原点的距离为5,分别确定反比例函数和一次函数的解析式.
答案:先把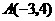 代入
代入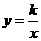 中,求出
中,求出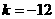 .
. 反比例函数
反比例函数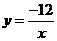 .
.
又 与
与 轴交点为
轴交点为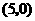 或
或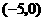
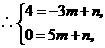
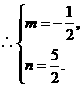 或
或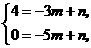
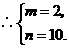
故一次函数解析式为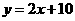 或
或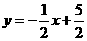 .
.
第19题. 已知正比例函数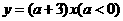 与反比例函数
与反比例函数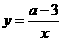 的图象有两个公共点,其中一个公共点的纵坐标为4.
的图象有两个公共点,其中一个公共点的纵坐标为4.
(1)求这两个函数的解析式;
(2)在坐标系中画出它们的图象(可不列表).
答案:(1)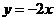 和
和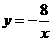
(2)图略
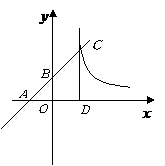
第20题. 如图,已知一次函数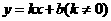 的图象与
的图象与 轴,
轴,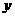 轴分别交于
轴分别交于 ,
,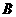 两点,且与反比例函数
两点,且与反比例函数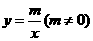 的图象在第一象限交于
的图象在第一象限交于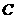 点,
点,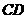 垂直
垂直 轴,垂足为
轴,垂足为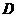 .若
.若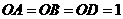 .
.
(1)求点 ,
, ,
, 的坐标;
的坐标;
(2)求一次函数和反比例函数的解析式.
答案:(1)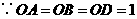 ,
, 点
点 ,
,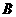 ,
,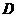 的坐标分别为
的坐标分别为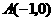 ,
,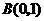 ,
,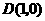 .
.
(2) 点
点 ,
,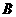 在一次函数
在一次函数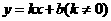 上,
上,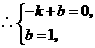 解得
解得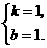
 一次函数解析式为
一次函数解析式为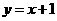 .
.
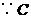 在一次函数
在一次函数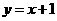 的图象上且
的图象上且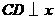 轴.
轴.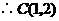 .
.
又点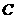 在
在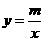 上,
上,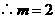 .故反比例函数解析式为
.故反比例函数解析式为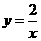 .
.
第21题. 在同一坐标系中画出函数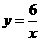 和
和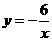 的图象.
的图象.
答案: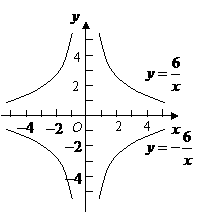
第22题. 下列各函数中,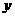 随
随 增大而增大的是( )
增大而增大的是( )
A.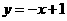 . B.
. B.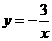 . C.
. C.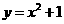 . D.
. D.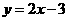 .
.
答案:D
第23题. 已知反比例函数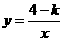 ,分别根据下列条件求出字母
,分别根据下列条件求出字母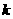 的取值范围:(1)函数图象位于第一、三象限;(2)在每一象限内,
的取值范围:(1)函数图象位于第一、三象限;(2)在每一象限内,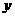 随
随 的增大而增大.
的增大而增大.
答案:(1)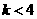 (2)
(2)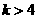
第24题. 已知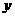 与
与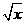 成反比例,且点
成反比例,且点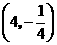 在它的图象上,求
在它的图象上,求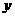 与
与 间的函数关系式.
间的函数关系式.
答案:解:设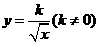 ,
,
把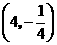 代入上式,得
代入上式,得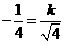 ,解得
,解得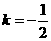 .
.
 反比例函数解析式为
反比例函数解析式为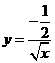 ,即
,即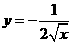 .
.
第25题. 反比例函数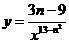 的图象所在象限内,
的图象所在象限内,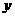 随
随 的增大而增大,求
的增大而增大,求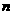 的值.
的值.
答案: 反比例函数必须满足
反比例函数必须满足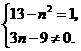 又
又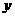 随
随 的增大而增大,
的增大而增大,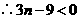 .
.
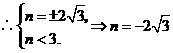 .
.
注意: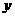 随
随 增大而增大
增大而增大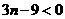 就已考虑到
就已考虑到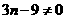 ,故
,故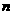 满足
满足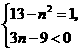 即可.
即可.
第26题. 已知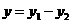 ,
,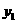 与
与 成反比例,
成反比例,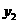 与
与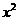 成正比例,且当
成正比例,且当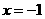 时,
时,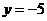 ;
;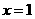 时,
时,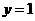 ,求
,求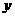 与
与 之间的函数关系式.
之间的函数关系式.
答案:解:
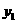 与
与 成反比例,
成反比例,
 设
设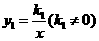 .
.
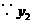 与
与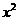 成正比例,
成正比例,
 设
设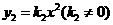 .
.
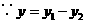 ,
,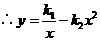 . ①
. ①
把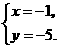 和
和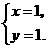 分别代入①,得
分别代入①,得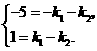
解得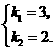
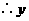 与
与 的函数解析式为
的函数解析式为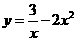 .
.
第27题. 已知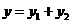 ,
,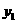 与
与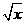 成正比例,
成正比例,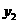 与
与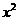 成反比例,当
成反比例,当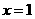 时,
时,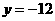 ,当
,当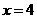 时,
时,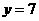 .
.
(1)求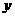 与
与 的函数关系式和
的函数关系式和 的取值范围;(2)当
的取值范围;(2)当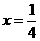 时,求
时,求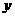 的值.
的值.
答案:①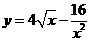 (
(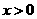 )②
)②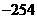
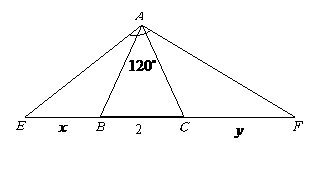
第28题. 如图,已知△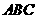 是边长为2的等边三角形,点
是边长为2的等边三角形,点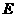 ,
,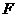 分别在
分别在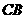 和
和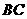 的延长线上,且
的延长线上,且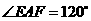 ,设
,设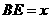 ,
,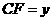 ,求
,求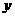 与
与 的函数关系,并画出这个函数图象(如图).
的函数关系,并画出这个函数图象(如图).
答案: △
△ △
△ ,函数式
,函数式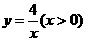 .
.
图象如图.
第29题. 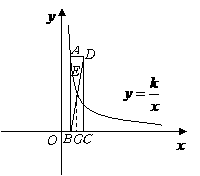 如图所示,已知点
如图所示,已知点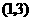 在函数
在函数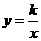
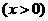 的图象上,矩形
的图象上,矩形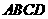 的边
的边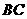 在
在 轴上,
轴上,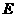 为对角线
为对角线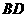 的中点,函数
的中点,函数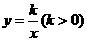 的图象又经过
的图象又经过 ,
,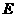 两点.点
两点.点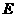 的横坐标为
的横坐标为 ,解答下列问题:
,解答下列问题:
(1)求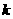 的值;
的值;
(2)求点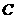 的横坐标(用
的横坐标(用 表示);
表示);
(3)当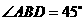 时,求
时,求 的值.
的值.
答案:解:(1) 函数
函数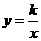 的图象过点
的图象过点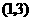 ,
,
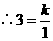 ,
,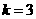 .
.
(2) 当
当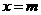 时,
时,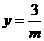 .
.

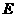 点的坐标为
点的坐标为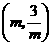 .
.
作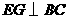 ,
,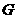 为垂足.
为垂足.
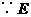 是
是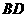 的中点,
的中点,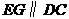 ,
,

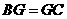 .
.
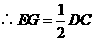 .
.
 点
点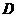 的纵坐标为
的纵坐标为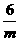 .
.
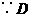 ,
, 两点纵坐标相等,
两点纵坐标相等,
 点
点 的纵坐标为
的纵坐标为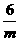 .
.
又 点
点 在双曲线
在双曲线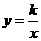 上,即在
上,即在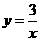 上.
上.
当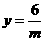 时,有
时,有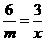 .
.
解得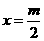 .
.
 点
点 的坐标为
的坐标为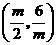 .
.
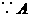 ,
,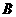 两点的横坐标相等.
两点的横坐标相等.
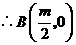 .
.
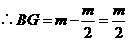 .
.
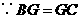 ,
,
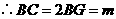 .
.
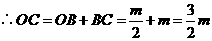 .
.
 点
点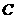 的横坐标为
的横坐标为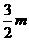 .
.
(3)当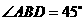 时,
时,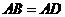 ,
,
则有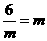 ,即
,即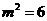 .
.
解得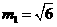 .
.
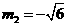 (不合题意,舍去).
(不合题意,舍去).
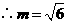 .
.
第30题. 已知直线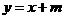 和双曲线
和双曲线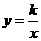 的一个交点为
的一个交点为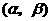 .其中
.其中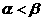 ,并且
,并且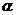 ,
,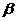 是方程
是方程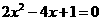 的两个实数根,求这两图象的解析式.
的两个实数根,求这两图象的解析式.
答案:此题通过求交点坐标解题较繁,用根与系数关系比较简单,把交点坐标(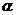 ,
,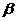 )代入两解析式,并变形,得
)代入两解析式,并变形,得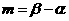 ,
,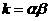 ,
,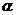 ,
,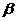 是方程
是方程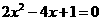 的根,不难算出
的根,不难算出 ,
, 的值.
的值.
结果是: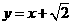 ;
;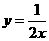 .
.
第31题. 如图所示,直线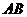 过点
过点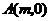 ,
,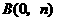 ,
,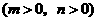 ,反比例函数为
,反比例函数为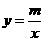 的图象与
的图象与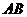 交于
交于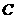 ,
,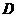 两点,
两点,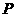 为双曲线
为双曲线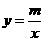 上任意一点,过
上任意一点,过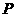 作
作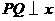 轴于
轴于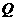 ,
,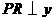 轴于
轴于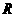 ,请分别按(1)、(2)、(3)的要求解答问题.
,请分别按(1)、(2)、(3)的要求解答问题.
(1)若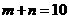 ,
,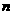 为何值时△
为何值时△ 的面积最大?最大值是多少?
的面积最大?最大值是多少?
(2)若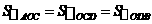 ,求
,求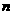 的值;
的值;
(3)在(2)的条件下,过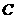 ,
, ,
,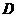 三点作抛物线,当该抛物线的对称轴为
三点作抛物线,当该抛物线的对称轴为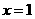 时,矩形
时,矩形 的面积是多少?
的面积是多少?
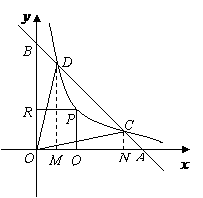
答案:解:(1)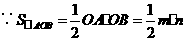 ,
,
又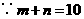 ,
,
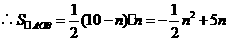

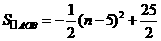 .
.
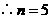 时,△
时,△ 面积最大,最大值为
面积最大,最大值为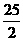 .
.
(2)分别过 ,
,试题详情
观察下列单项式:-x,2x2,-3x3,4x4,…,-19x19,20x20,…,你能写出第n个单项式吗?并写出第2001个单项式。
为了解决这个问题,我们不妨从系数和次数两个方面入手进行探索,从中发现规律,经过归纳,猜想出结论.
(1) 系数的规律有两条:①系数的符号规律是_____________.②系数的绝对值规律是______.
(2) 次数的规律是______________.
(3)根据上面的归纳,可以猜想出第n个单项式是________.
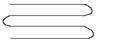
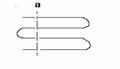
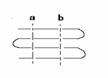
4. 一根绳子弯曲成如图(1)所示的形状,当用剪刀像如图(2)所示那样沿虚线a把绳子剪断时,绳子被剪为5段;当用剪刀像如图(3)所示那样沿虚线b(b∥a)把绳子再剪一次时,绳子就被剪为9段.若用剪刀在虚线a、b之间把绳子再剪(n-2)次(剪刀的方向与a平行),这样一共剪n次时绳子的段数是多少?
.
3.小红和父母三人准备参加旅行团外出旅游,甲旅行社告示知:“父母全票,女儿按5折优惠”;乙旅行社告知:“家庭旅游可按团体票计价,即每人均按全价的8折收费”.若这两家旅行社每人的原票价相同,服务质量也相同,你认为他们应该选哪家旅行社才使票价较为便宜?并请你说明理由.
2.已知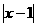 +(y+2)2=0,求
+(y+2)2=0,求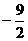 x3y2-
x3y2-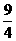 xy+
xy+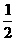 x3y2-
x3y2-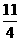 xy-x3y-5的值.
xy-x3y-5的值.
1.当x=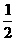 时,求-5+x2-5x-x2+3x+4的值.
时,求-5+x2-5x-x2+3x+4的值.
8.若a<0,ab<0,则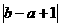 +
+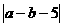 的值是_______.
的值是_______.
7. 下列式子2a+3,4a+6,8a+12,16a+24……后面将出现哪一个式子_________
6.如果A=x3-2x2+1,B=2x2-3x-1,则B+A=_________.
5.已知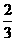 x3m-1y3
与
x3m-1y3
与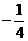 x5y2n-1是同类项,则5m+3n=________.
x5y2n-1是同类项,则5m+3n=________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com