
题目列表(包括答案和解析)
5.化简x-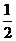 (x-1)的结果是( )
(x-1)的结果是( )
A.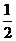 x+
x+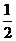 B.
B.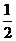 x-
x-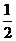 C.
C.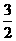 x-1 D.
x-1 D.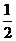 x+1
x+1
4.单项式4x5y与2x2(-y)3z的积是( )
A.8x10y3z B.8x7(-y)4z C.-8x7y4z D.-8x10y3z
3.已知-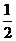 a2b·mab2=-3a3b3,则m等于( )
a2b·mab2=-3a3b3,则m等于( )
A.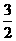 B.6 C.-
B.6 C.-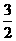 D.-6
D.-6
2.下面的计算对不对?如果不对,应怎样改正?
(1)3a2·4a3=7a5; (2)2x3·3x4=5x12; (3)3m2·(-5m2)=-15m2.
1.(1)2x5·5x2=_________; (2)2ab2·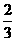 a3=________;
a3=________;
(3)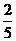 x2y3·
x2y3·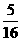 xyz=_________;
(4)3x2y(-4xy2)·(x3)2=_________.
xyz=_________;
(4)3x2y(-4xy2)·(x3)2=_________.
2.单项式与多项式相乘,类似乘法分配律.
范例积累
[例1]计算:
(1)3b3·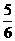 b2; (2)(-6ay3)(-a2);
b2; (2)(-6ay3)(-a2);
(3)(-3x)3·(5x2y); (4)(2×104)(6×103)·107.
[解](1)3b3·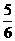 b2=(3×
b2=(3×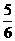 )(b3·b2)=
)(b3·b2)=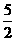 b5;
b5;
(2)(-6ay3)(-a2)=[(-6)×(-1)]×(a·a2)·y3=6a3y3;
(3)(-3x)3·(5x2y)=(-27x3)·(5x2y)=-135x5y;
(4)(2×104)(6×103)·107=(2×6)(104×103×107)=1.2×1015.
[注意](1)单项式的乘法应遵循“符号优先”,先确定符号,再把它们的绝对值相乘.
(2)单项式与单项式相乘,若它们的系数为带分数,应化为假分数,再相乘,且最后结果的系数若是带分数应化为假分数.
[例2]计算:
(1)2a2b(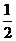 ab-3ab2); (2)(
ab-3ab2); (2)(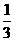 x-
x- xy)·(-12y).
xy)·(-12y).
[解](1)2a2b(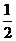 ab-3ab2)
ab-3ab2)
=2a2b·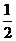 ab+2a2b·(-3ab2)
ab+2a2b·(-3ab2)
=a3b2-6a3b3;
(2)(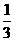 x-
x- xy)·(-12y)
xy)·(-12y)
=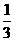 x·(-12y)+(-
x·(-12y)+(- xy)·(-12y)
xy)·(-12y)
=-4xy+9xy2.
[注意](1)单项式与多项式相乘时,注意要漏乘多项式中的常数项.
(2)相乘时,注意符号.
基础训练
1.几个单项式相乘时,积的符号由负因式的个数决定:偶正、奇负.
2.掌握单项式与多项式的相乘法则.
[学法指导]
1.掌握单项式的乘法法则.
5.2 单项式的乘法 同步练习
[知识提要]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com