4.下列由四舍五入得到的数各精确到哪一位?各有哪几个有效数字?

(1)54.9；　　 (2)0.070 8；　　 (3)6.80万；　　 (4)1.70×10⁶

思路解析：(1)6.80万不能说精确到百分位，因为6.80万后有个万字.(2)1.70×10⁶也不能说精确到百分位.应先把1.70×10⁶=1 700 000，再看7后的0所在的数位，即精确到万位.

答案：(1)54.9精确到十分位(即精确到0.1)，有三个有效数字：5，4，9；

(2)0.070 8精确到万分位(即精确到0.0001)，有三个有效数字：7，0，8；

(3)6.80万精确到百位，有三个有效数字：6，8，0；

(4)1.70×10⁶精确到万位，有三个有效数字：1，7，0.

3.用四舍五入法取近似值，396.7精确到十位的近似数是________；保留两个有效数字的近似数是_______.

思路解析：本题中，精确到十位以上或保留两个有效数字应用科学记数法.

答案：4.0×10²　 4.0×10²

2.用四舍五入法得到的近似值0.380精确到________位，48.68万精确到_______位.

思路解析：看最后一位数字在哪一数值上即为精确到该值.

答案：千分　 百

1.用四舍五入法取近似值，0.012 49精确到0.001的近似数是______，保留三个有效数字的近似数是______.

思路解析：注意，精确到0.001实际就是精确到千分位，也就是把万分位上的数字用“四舍五入”的方法，去掉千分位以后的数字.保留有效数字时注意计算有效数字是从左边第一个不是零的数字起，到最后一位数字止的.

答案：0.012　 0.0125.

3.判断下列各题中哪些是精确数，哪些是近似数.

(1)某班有32人；

(2)半径为10 cm的圆的面积约为314 cm²；

(3)张明的身高约为1.62米；

(4)取π为3.14.

思路解析：完全准确的数是精确数.如某班有32人，5枝铅笔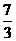，等都是准确数.在解决实际问题时，往往只能用近似数.有时搞的完全准确没有必要；有时测得准确很困难.

答案：(1)32人是精确数.(2)(3)(4)都是近似数.

10分钟训练(强化类训练，可用于课中)

2.填空

(1)一般地，一个近似数，四舍五入到哪一位，就说这个近似数_______到哪一位；

(2)一个近似数，从左边第一个不是0的数字起，到末位数字止，所有的数字都叫做这个数的_________；

(3)除了四舍五入法，常用的近似数的取法还有两种，_______和_______.

思路解析：利用近似数完成问题.

答案：(1)精确

(2)有效数字

(3)进一法　 去尾法

1.(2010四川内江模拟)台湾是我国最大的岛屿，总面积为35 989.76平方千米.用科学记数法应表示为(保留三个有效数字)(　　 )

A.3.59×10⁶平方千米　　　 B.3.60×10⁶平方千米

C.3.59×10⁴平方千米　　　 D.3.60×10⁴平方千米

答案：D

1.5.3　 近似数和有效数字

5分钟训练(预习类训练，可用于课前)

15.某中学图书馆将图书分为自然科学、文学艺术、社会百科、数学四类．在“深圳读书月”活动期间，为了了解图书的借阅情况，图书管理员对本月各类图书的借阅量进行了统计，频率分布表和图22-2-21是图书管理员通过采集数据后，绘制的两幅不完整的频率分布表与频数分布直方图．请你根据图表中提供的信息，解答以下问题:

频率分布表

(1)补全频率分布表中的空格；

(2)在图22-2-21中，将表示“自然科学”的部分补充完整；

图22-2-21

(3)若该学校打算采购一万册图书，请你估算“数学”类图书应采购多少册较合适？

分析：可算出数据总数为400÷0.2＝2 000(册)，由频率之和为1，算得“数学”的频率为1－0.2－0.5－0.25＝0.05，所以“数学”的频数为2 000×0.05＝100．

解：(1)100　 0.05　 (2)如图　 (3)10 000×0.05＝500．

本章整合

知识建构

数学趣闻

统计结果的误用

　　 统计资料表明：大多数汽车事故出在中等速度行驶中，极少的事故是出在大于150千米／小时的行驶速度上的．这是否意味着高速行驶比较安全?绝对不是这样，统计关系往往不能表明因果关系.由于多数人是以中等速度开车，所以多数事故是出在中等速度的行驶中．统计资料还表明：在亚利桑那州死于肺结核的人比其他州的人多．这是否意味着亚利桑那州的气候易生肺结核病?正好相反，该州气候对患肺结核病的人有好处，所以他们纷纷前来，自然就使这个州死于肺结核的平均数升高了．

体验与收获

____________________________________________________________________________

____________________________________________________________________________

____________________________________________________________________________

____________________________________________________________________________

____________________________________________________________________________

____________________________________________________________________________

____________________________________________________________________________

14.为了了解某校九年级500名学生的视力情况，现从中随机抽测了若干名学生的视力作为样本进行数据处理，并绘出频率分布直方图(如图22-2-20)：

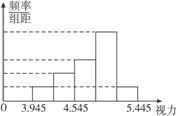
图22-2-20

已知学生的视力都大于3.95而小于5.40(均为3个有效数字)，图中从左到右五个小长方形的高的比为1∶2∶3∶5∶1．视力最好的一组的频数为5，请你回答以下问题：

(1)共抽测了多少名学生？

(2)若视力不低于4.85属视力正常，低于4.85属视力不正常，在抽测的学生当中，视力正常的占百分之几？

(3)根据抽样调查结果，请你估算该校九年级学生当中，大约有多少名学生视力不正常？

分析：频率分布直方图中小长方形的高的比为各组频率之比，也为各组频数之比，由最后一组频数为5，知每一份为5人．再由直方图可算出组距为0.3．

解：(1)5+2×5+3×5+5×5+5＝60(人)．(2)视力正常的应为第四、五组，人数为5×5+5＝30，所以视力正常的占30÷60＝50%．(3)500×50%＝250(人)．