6.由于看错了运算符号，“小马虎”把一个整式减去多项式2ab-3bc+4，误认为加上这个多项式，结果得出答案是2bc-1-2ab，问原题答案是多少？

　思路解析：因为把“减去”看成了“加上”，即所求整式加2ab-3bc+4等于2bc-1-2ab，用加减互逆运算，即可求出这个整式.

　解：由题意得所求整式为

　(2bc-1-2ab)-(2ab-3bc+4)＝2bc-1-2ab-2ab+3bc-4＝-4ab+5bc-5.

　∴正确答案是

　(-4ab+5bc-5)-(2ab-3bc+4)＝-4ab+5bc-5-2ab+3bc-4＝-6ab+8bc-9.

5.已知A＝x³-2x²+x-7，B＝6x²-8x+4，C＝x³-2x²-9，

　求：(1)A-2B+C；(2)4A-2B+3C.　

　思路解析：本题考查整式的运算，注意加括号.

　解：(1)A-2B+C＝(x³-2x²+x-7)-2(6x²-8x+4)+(x³-2x²-9)= 2x³-16x²+17x-24；

　(2)4A-2B+3C＝4(x³-2x²+x-7)-2(6x²-8x+4)+3(x³-2x²-9)=7x³-26x²+20x-63.

4.计算：

　(1) 2(x+1)-x；

　(2)-5(x²-3)-2(3x²+5).

　思路解析：在去括号时要注意符号，要把括号里的每一项都乘以前边的系数.

　答案：(1)x+2　(2)-11x²+5

综合·应用·创新

3.老师在课堂上出了一道题：当x＝34 689，y＝0.156 93时，求5x³-7x³y+3x²y+2x³+7x³y-3x²y-7x³的值.当很多同学拿出计算器计算时，有一位同学却很快算出了答案，他求出的值是________________.

　思路解析：代数式的求值要先化简，先进行整式的加减，得到的值为0，与x、y的值无关.

　答案：0

2.把下列各式分别填在相应的大括号内：-x,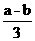，a²-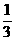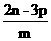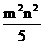，，，-7，9.

　单项式：{　　　　…}，

　多项式：{　　　　…}，

　整式：{　　　　…}.

　思路解析：根据定义分类填空.

　答案：单项式：{-x，-7，9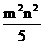，，…}，多项式：{a²-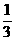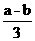，，…}，整式：{-x，-7，9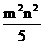，，a²-，，…}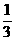

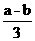1.如果M和N都是3次多项式，则M+N一定是(　)

　A.3次多项式

　B.6次多项式

　C.次数不低于3的多项式或单项式

　D.次数不高于3的多项式或单项式

　思路解析：多项式相加，实质是合并同类项，结果的次数不会增加，若系数互为相反数的同类项合并，这些项就为0.

　答案：D

6.桌上放着8只茶杯，全部杯口朝上，每次翻转其中4个，只要翻转两次，就可以把它们全都翻成杯口朝下.

如果将问题中的8只茶杯改为6只，每次仍然翻转其中的4只，能否经过若干次翻转把它们全部翻成杯口朝下?

请你动手试验一下.

提示：用+1表示杯口朝上，－1表示杯口朝下，请填出翻转次数及过程:

初始状态 +1，+1，+1，+1，+1，+1.

第一次翻转 －1，－1，－1，－1，______，__________

________　 ______________________________________

________　 ______________________________________

……

答案：答案不唯一?

6只茶杯：翻转三次可以全部翻成杯口朝下.

第一次翻转为-1，-1，-1，-1，+1，+1；

第二次翻转为-1，+1，+1，+1，-1，+1；

第三次翻转为-1，-1，-1，-1，-1，-1.

5.把下列各数填在相应的集合内：15，－6，+2，－0.9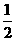，，0，0.23，－1，.

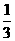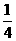正数集合{____________…}；

负数集合{____________…}；

正分数集合{____________…}；

负分数集合{____________…}?

思路解析：此题主要考查你对数的分类能力.正数包括正整数和正分数；负数包括负整数和负分数；正分数包括正分数本身外，还有正的小数；同样，负的小数也属于负分数；另外，填整数集合时，不要漏掉“0”.填集合时通常最后要加省略号.

答案：正数集合{15，+2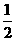，，0.23，，…}；

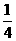负数集合{－6，－0.9，－1，…}；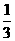

正分数集合{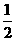，0.23，，…}；

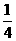负分数集合{－0.9，－1，…}?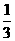

4.填空：

(1)如果零上3　 ℃记作+3　 ℃，那么－7　 ℃表示的意义是____________；

(2)某钢厂增产150吨钢记作+150吨，那么减产30吨记作____________；

(3)如果前进5千米记作+5千米，那么后退16千米记作_____________；

(4)支出100元记作－100元，那么+1 000元表示的意义是_____________.

思路解析：利用相反意义的量来解决实际问题.

答案：(1)零下7　 ℃　 (2)－30吨　 (3)－16千米　 (4)收入1 000元

3.用正数和负数表示下列具有相反意义的量.

(1)温度上升5　 ℃和温度下降7　 ℃；

(2)向东6米和向西10米；

(3)球赛时，如果胜一场得1分，败一场扣1分；

(4)海平面以上200米和海平面以下30米.

思路解析：习惯规定上升、向东、得分、高出等记作正.

答案：(1)+5　 ℃和－7　 ℃　 (2)+6米和－10米

(3)+1和－1　 (4)+200米和－30米