
题目列表(包括答案和解析)
1.去括号后括号内各项符号是否变号,关键是看括号前面的符号.若是“+”号,各项符号不变;若是“-”号,各项符号都要改变.
2.添括号的法则.
思维点击
1.去括号的法则.
3.5 去括号
知识平台
9.1《平行四边形的性质》同步练习
第1题. 如图,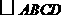 中,
中,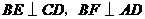 ,垂足分别为
,垂足分别为 ,
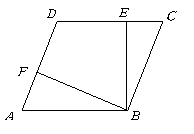
,
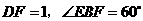 ,求
,求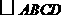 的面积.
的面积.
答案:解: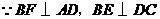 ,则
,则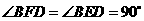 .
.
又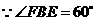 ,
,
且根据四边形的内角和为 ,可知
,可知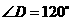 .
.
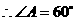 .
.
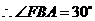 ,则
,则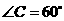 .
.
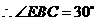 .
.
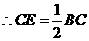 ,由于
,由于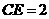 ,
,
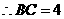 .
.
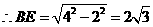 .
.
又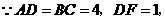
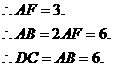
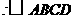 的面积为
的面积为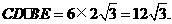
第2题. 如图,在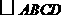 中,对角线
中,对角线 与
与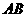 垂直,
垂直,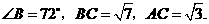
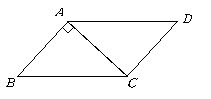 (1)求
(1)求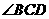 ,
,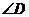 的度数.(2)求
的度数.(2)求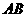 的长及
的长及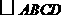 的周长.
的周长.
答案:解:(1) 在
在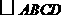 中,
中,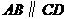 ,
,
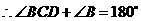 .
.
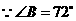 ,
,
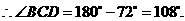
又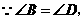
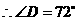 .
.
(2)在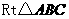 中,
中,
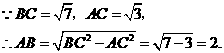
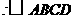 的周长为
的周长为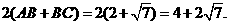
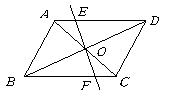
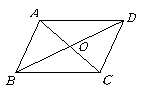
第3题. 如图所示,已知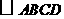 ,对角线
,对角线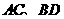 相交于点
相交于点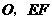 是过点
是过点 的任一直线,交
的任一直线,交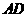 于点
于点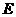 ,交
,交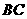 于
于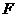 ,试说明
,试说明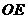 与
与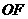 之间的关系,并说明理由.
之间的关系,并说明理由.
答案:解: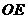 与
与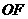 相等,理由如下:
相等,理由如下:
 四边形
四边形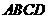 是平行四边形,
是平行四边形,
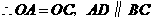 .
.
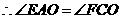 ,在
,在 与
与 中,
中,
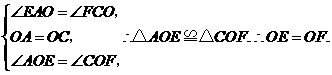
 第4题. 已知
第4题. 已知 的周长为24cm,
的周长为24cm, 相交于
相交于 ,且
,且 的周长比
的周长比 的周长小2.如图所示,求
的周长小2.如图所示,求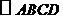 各边的长?
各边的长?
答案:解: 的周长
的周长 ,
,
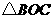 的周长
的周长 ,
,
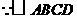 ,
,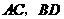 交于
交于 .
.
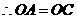 ,
,
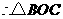 的周长-
的周长- 的周长=
的周长=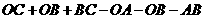
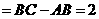 .
.
又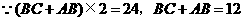 .
.
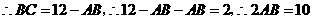 .
.
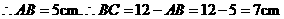 .
.
第5题. 已知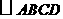 的一个内角
的一个内角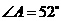 ,求
,求 的度数.
的度数.
答案:解: 四边形
四边形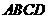 是平行四边形,且
是平行四边形,且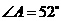 ,
,
则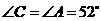 .
.
第6题.  如图所示,四边形
如图所示,四边形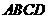 是平行四边形,
是平行四边形,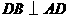 ,且
,且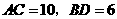 ,求四边形各边的长.
,求四边形各边的长.
答案:解: 四边形
四边形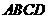 是平行四边形.
是平行四边形.
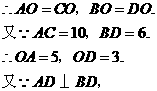
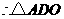 是
是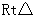 .
.
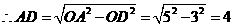 .
.
在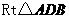 中,
中,
第7题. 若平行四边形 的对角线
的对角线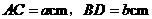 .且
.且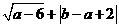
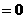 ,则下列哪个长度能作为平行四边形的一条边的长度( )
,则下列哪个长度能作为平行四边形的一条边的长度( )
A.1 B.5 C.3.5 D.7
答案:C
第8题. 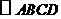 的对角线
的对角线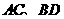 相交于
相交于 ,若
,若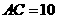 cm,则
cm,则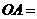 ( )
( )
A.3cm B.4cm C.5cm D.6cm
答案:C
第9题. 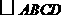 中,
中,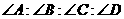 的值可以是( )
的值可以是( )
A.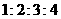 B.
B.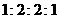 C.
C.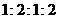 D.
D.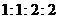
答案:C
第10题. 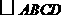 的周长为48cm,两邻边之差为8cm,且
的周长为48cm,两邻边之差为8cm,且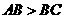 ,求得
,求得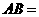 ,
,
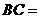 .
.
答案:16cm 8cm
第11题. 如图所示,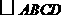 中,
中,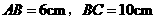 ,
,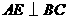 垂足为
垂足为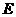 ,
,
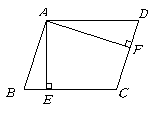
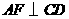 垂足为
垂足为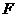 .已知:
.已知: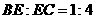 .求
.求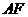 的长.
的长.
答案:解: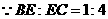 ,设
,设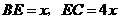 .
.
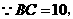
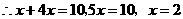 ,
,
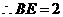 cm.
cm.
又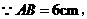
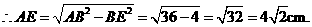

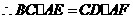
即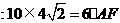 .
.
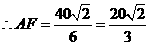 cm.
cm.
第12题. 如图所示,在 中,
中,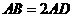 ,且
,且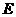 为
为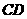 的中点,求
的中点,求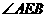 的度数.
的度数.
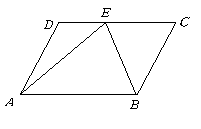
答案:解:四边形 是平行四边形,
是平行四边形,
 .
.
 ,
,
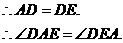
又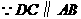 ,
,
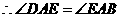 .
.
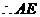 是
是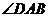 的角平分线,同理
的角平分线,同理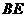 是
是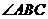 的角平分线.
的角平分线.
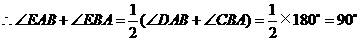 .
.
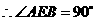 .
.
第13题.  为
为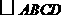 的对角线
的对角线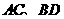 的交点,
的交点,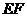 经过点
经过点 ,且与边
,且与边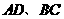 分别交于点
分别交于点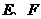 ,若
,若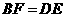 ,则图中的全等三角形最多有( )
,则图中的全等三角形最多有( )
A.2对 B.3对 C.5对 D6对.
答案:D
第14题. 如图,在 中,
中,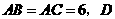 是
是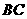 上的点,
上的点,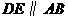 交
交 于点
于点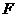 ,
,
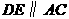 交
交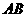 于
于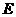 ,那么四边形
,那么四边形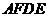 的周长为( )
的周长为( )
A.6 B.12 C.18 D.24

答案:B
第15题. 如图,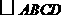 的周长为20cm,对角线
的周长为20cm,对角线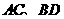 相交于点
相交于点 的周长比
的周长比 的周长大2cm,那么
的周长大2cm,那么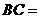 cm.
cm.
答案:6
第16题. 在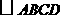 中,对角线
中,对角线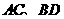 相交于点
相交于点 ,已知
,已知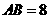 cm,
cm,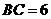 cm,
cm, 周长为18cm,那么
周长为18cm,那么 的周长为 cm.
的周长为 cm.
答案:16
第17题. 如果平行四边形的两条对角线长分别是8和12,那么它的边长不能是( )
A.10 B.8 C.7 D.6
答案:A
第18题. 以不在同一直线上的三点为顶点作平行四边形,最多能作( )
A.4个 B.3个 C.2个 D.1个
答案:B
第19题.  为等腰
为等腰 底边
底边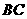 上一点,
上一点,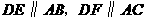 ,则四边形
,则四边形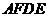 的周长是( )
的周长是( )
A.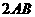 B.
B.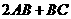 C.
C.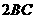 D.
D.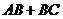
答案:A
第20题. 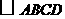 中,
中,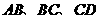 的长度分别为
的长度分别为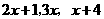 ,则
,则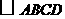 的周长是 .
的周长是 .
答案:32
第21题. 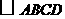 中,
中,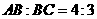 ,周长是28cm,则
,周长是28cm,则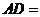 ,
,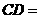 .
.
答案:6cm,8cm
第22题. 如下图如何在一个平行四边形内画一条线段,把这个平行四边形的面积二等分.(至少画出4种)

答案:经过对角线交点的任一条线段

第23题. 平行四边形两邻边上的高为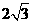 和
和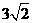 ,这两条高的夹角为
,这两条高的夹角为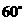 ,则这个平行四边形的周长是 .
,则这个平行四边形的周长是 .
答案: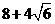
第24题. 如果一个平行四边形的一边长是8,一条对角线长为6,那么它的另一条对角线 的取值范围是 .
的取值范围是 .
答案: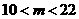
第25题. 如图,四边形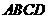 是平行四边形.对角线
是平行四边形.对角线 、
、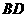 交于点
交于点 ,过点
,过点 画直线
画直线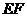 ,分别交
,分别交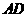 、
、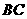 于点
于点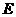 、
、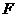 .
.
 求证:
求证: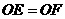 .
.
答案:证明: 四边形
四边形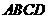 是平行四边形
是平行四边形
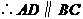 ,
,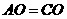
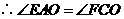
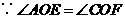
 △
△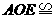 △
△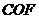
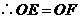
第26题. 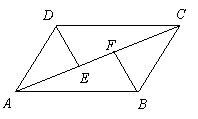 如图,
如图, 是
是 对角线
对角线 上两点,且
上两点,且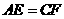 ,连结
,连结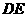 、
、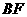 ,则图中共有全等三角形的对数是
,则图中共有全等三角形的对数是
A.1对 B.2对 C.3对 D.4对
答案:C
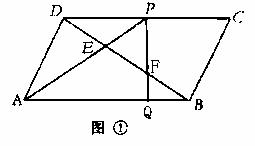
第27题. E、F为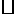 ABCD的对角线DB上三等分点,连AE并延长交DC于P,连PF并延长交AB于Q,如图①.
ABCD的对角线DB上三等分点,连AE并延长交DC于P,连PF并延长交AB于Q,如图①.
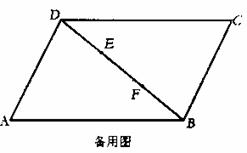
(1)在备用图中,画出满足上述条件的图形,记为图②.试用刻度尺在图①、②中量得AQ,BQ的长度,估计AQ,BQ间的关系,并填入下表.
长度单位:cm
|
|
AQ长度 |
BQ长度 |
AQ、BQ间的关系 |
|
图①中 |
|
|
|
|
图②中 |
|
|
|
由上表可猜测AQ、BQ间的关系是__________________.
(2)上述(1)中的猜测AQ,BQ间的关系成立吗?为什么?
(3)若将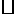 ABCD改为梯形(AB∥CD)其他条件不变,此时(1)中猜测AQ,BQ间的关系是否成立?(不必说明理由)
ABCD改为梯形(AB∥CD)其他条件不变,此时(1)中猜测AQ,BQ间的关系是否成立?(不必说明理由)
答案:
|
|
AQ长度 |
BQ长度 |
AQ、BQ间的关系 |
|
图①中 |
2.7 |
0.9 |
AQ=3BQ |
|
图②中 |
3.3 |
1.1 |
AQ=3BQ |
解:(1)
注:测量数据基本接近上表中的数据,均可得分.
猜测:AQ=3QB.
(2) 成立.
 四边形
四边形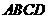 为平行四边形,
为平行四边形,
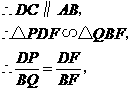
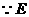 、
、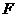 为
为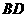 三等分点,
三等分点,
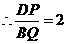 .
.
同理 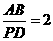 .
.
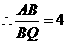 ,
,
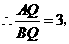 即
即 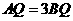 .
.
(3)成立.
第28题. 小明想从一个平行四边形纸板上剪三个三角形,要求使其中两个三角形的面积相等,别一个三角形面积是这两个三角形面积的2倍,他该如何剪才能符合要求?如图所示.
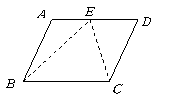
答案:解:在 边上找取中点
边上找取中点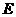 ,连结
,连结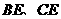 ,得到三个三角形,
,得到三个三角形,
沿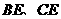 剪开即可.
剪开即可.
理由如下: 四边形
四边形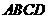 是平行四边形.
是平行四边形.
故 中的
中的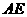 边上的高,
边上的高,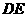 边上的高,
边上的高,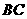 边上的
边上的
高均相等.
又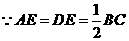 .
.
故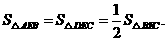
第29题. 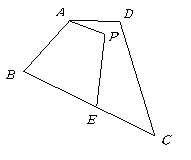 如图所示,四边形
如图所示,四边形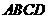 内有一条折线
内有一条折线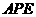 ,你能否从
,你能否从 点画一条直线使这条直线分成的四边形的面积,左边的面积是折线
点画一条直线使这条直线分成的四边形的面积,左边的面积是折线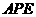 右边的面积,直线右边的面积仍是折线
右边的面积,直线右边的面积仍是折线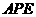 右边的面积.
右边的面积.
答案:解:连结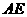 ,过
,过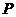 点作
点作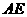 的平行线,交
的平行线,交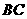 于
于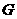 ,连结
,连结 ,
,
则直线 即为所求.
即为所求.
理由如下:
 .
.
故:折线变为直线后,两边的面积没有变化.
第30题. 平行四边形相邻两边之比为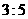 ,它的周长是32cm,则这个平行四边形较长边为 cm.
,它的周长是32cm,则这个平行四边形较长边为 cm.
答案:10
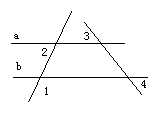
2.( 10分)如图,a∥b,∠1=122°,∠3=50°,求∠2和∠4的度数。
1.(6分)作图题(不写作法,保留作图痕迹)
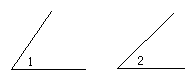 已知:∠1、∠2。
已知:∠1、∠2。
求作:∠AOB,使∠AOB=2∠2-∠1
5.下列说法正确的是( )
A.相等的角是对顶角 B.一对同旁内角的平分线互相垂直
C.对顶角的平分线在一条直线上 D.同位角相等
4.如图,直线AB与CD交于点O,OE⊥AB于O,图∠1与∠2的关系是( )
A.对顶角 B.互余 C.互补 D相等
3.已知:如图,∠1=∠2,则有( )
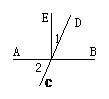 A.AB∥CD B.AE∥DF C. AB∥CD 且AE∥DF D.以上都不对
A.AB∥CD B.AE∥DF C. AB∥CD 且AE∥DF D.以上都不对
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com