9． 满足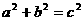的三个正整数，称为　　　　　　　　 。

字母所代表的正方形面积是　　　 。　　　　　　　　　　　　 A

8．如图，直角三角形中未知边的长度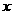=　　　 。5 　　　　　　　　64

6.　　 如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,

要爬行的最短路程(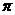取3)是(　 ) A.20cm;B.10cm;C.14cm;D.无法确定.　　 A

5.　　 将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是(　 )

A. 钝角三角形;　 B. 锐角三角形;　 C. 直角三角形;　 D. 等腰三角形.　　　　　　 B

4.　　 适合下列条件的△ABC中, 直角三角形的个数为(　 )

①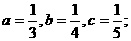②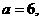∠A=45⁰;③∠A=32⁰, ∠B=58⁰;④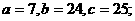

⑤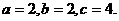　 A. 2个;　　 B. 3个;　　 C. 4个;　　 D. 5个.

3.　　 下列各组数中不能作为直角三角形的三边长的是(　 )

A. 1.5,2,3;　　　 B. 7,24,25;　　　 C. 6,8,10;　　　 D. 9,12,15.

2.　　 小丰的妈妈买了一部29英寸(74cm)的电视机,下列对29英寸的说法中正确的是(　 )

A. 小丰认为指的是屏幕的长度;　　　　　　 B. 小丰的妈妈认为指的是屏幕的宽度;

C. 小丰的爸爸认为指的是屏幕的周长;　　　 D. 售货员认为指的是屏幕对角线的长度.

1.　　 一个直角三角形,两直角边长分别为3和4,下列说法正确的是(　 )

A. 斜边长为25;　 B. 三角形的周长为25;　　 C. 斜边长为5;　 D. 三角形面积为20.

17．(1)如图，把一个等腰直角三角形ABC沿斜边上的高CD(裁剪线)剪一刀，从这个三角形中裁下一部分，与剩下部分能拼成一个四边形A′BCD(见示意图a)．

(以下有画图要求的，工具不限，不必写画法和证明)

①猜一猜：四边形A′BCD一定是　　　　　　 形；

②试一试：按上述的裁剪方法，请你拼一个与图(a)形状不同的四边形，并在图(b)中画出示意图．

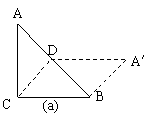
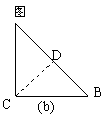
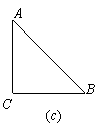
(2)在等腰直角三角形ABC中，请你找出与(1)不同的裁剪线，把分割成的两部分拼成特殊四边形．

①想一想：你能拼得的特殊四边形有　　　　　　　 ；

②画一画：请在图(c)中画出一个你拼得的特殊四边形示意图．

20、(本题满分10分)

已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.

(1)　 如图1, 连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请证明,若不正确请举反例说明;

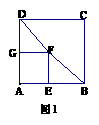
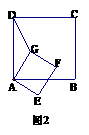(2)　 若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.

(本小题满分12分)

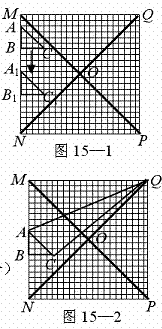
如图15-1和15-2，在20×20的等距网格(每格的宽和高均是1个单位长)中，Rt△ABC从点A与点M重合的位置开始，以每秒1个单位长的速度先向下平移，当BC边与网的底部重合时，继续同样的速度向右平移，当点C与点P重合时，Rt△ABC停止移动.设运动时间为x秒，△QAC的面积为y.

(1)如图15-1，当Rt△ABC向下平移到Rt△A₁B₁C₁的位置时，请你在网格中画出Rt△A₁B₁C₁关于直线QN成轴对称的图形；

(2)如图15-2，在Rt△ABC向下平移的过程中，请你求出y与x的函数关系式，并说明当x分别取何值时，y取得最大值和最小值？最大值和最小值分别是多少？

(3)在Rt△ABC向右平移的过程中，请你说明当x取何值时，y取得最大值和最小值？最大值和最值分别是多少？为什么？

(说明：在(3)中，将视你解答方法的创新程度，给予1~4分的加分)