
题目列表(包括答案和解析)
2.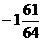 的立方根是( )
的立方根是( )
A.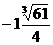 B.
B.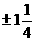 C.
C.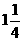 D.
D.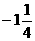
1.下列说法中,不正确的是( )
A.8的立方根是2 B.-8的立方根是-2
C.0的立方根是0 D.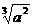 的立方根是
的立方根是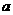
6.某商人将每件进价为80元的商品按100元出售,每天可售出30件.现在他为了尽快减少库存,决定采取适当降价措施来扩大销售量,增加日盈利.经市场调查发现,如果该商品每降价2元,那么平均每天可多售出10件.要想在销售这种商品上平均每天盈利800元,问每件商 品应降价多少元?
品应降价多少元?
5.一批彩电,经过两次降价后 价格由原来的每台2 250元降为1
440元.问平均每次降价的百分率是多少?
价格由原来的每台2 250元降为1
440元.问平均每次降价的百分率是多少?
3.一次会议上,每两个参加会议的人都相互握了一次手,有人统计一共握了66次手.这次会议到会的人数是多少?
4.我国是世界上受沙漠化危害最严重的国家之一,沙化土地面积逐年增长. 2000年初我
2000年初我 国沙化土地面积约为261.5万km2
国沙化土地面积约为261.5万km2 ,到2002年初沙化地面积已达近262万km2.假设沙化土地面积每年的增长率相同,那么增长率是多少?
,到2002年初沙化地面积已达近262万km2.假设沙化土地面积每年的增长率相同,那么增长率是多少?
2.某超市1月份的营业额是0.2亿元,第一季度的营业额共1亿元.如果平均每月增长率为x,则由题意列方程应为( ).
(A)0.2(1+x)2=1 (B)0.2+0.2×2x=1
(C)0.2+0.2×3x=1 (D)0.2×[1+(1+x)+(1+x)2]=1
1.党的十六大提出全面建设小康社 会,加快
会,加快 推进社会主义现代化,力争国民生产总值到2020年比2000年翻两番.在本世纪的前20年(2001-2020年),要实现这一目标,以10年为单位计算,设每10年的国民生产
推进社会主义现代化,力争国民生产总值到2020年比2000年翻两番.在本世纪的前20年(2001-2020年),要实现这一目标,以10年为单位计算,设每10年的国民生产 总值的增长率都是x,那么x满足的方程为( ).
总值的增长率都是x,那么x满足的方程为( ).
(A)(1+x)2=2 (B)(1+x)2=4
(C)1+2x=2  (D)(1+x)+2(1+x)=4
(D)(1+x)+2(1+x)=4
2.3 一元二次方程的应用(1)同步练习
解题示范
例 某农户种植花生,老品种花生的每公顷产量为2 000千克,出油率为50%(即每100千克花生可加工成花生油50千克).现种植新品种花生后,每公顷收获的花生可加工成花生油1 320千克,其中花生出油率的增长率是每公顷产量增长率的一半,求新品种 花生每公顷产量的增长率.
花生每公顷产量的增长率.
审题 本题已知老品种花生的每公顷产量与出油率、新品种花生每公顷可出油1 320千克,以及新品种花生的出油率的增长率与产量增长率的关系.未知新品种花生的每公顷产量及出油率.
方案 可设所求增长率为x,列表如下:
|
|
老品种 |
新品种 |
|
每公顷产量 |
2000千克 |
2000(1+x)千克 |
|
出油率 |
50% |
50%(1+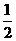 x) x) |
|
出油量 |
2000×50%千克 |
1320千克 |
从表中可寻找到相同对象的等量关系,从而可列出方程求解.
实施 设新品种花生 每公顷产量的增长率为x,则新品种花生出油率的增长率为x.根据题意,得2 000(1+x)·50%(1+
每公顷产量的增长率为x,则新品种花生出油率的增长率为x.根据题意,得2 000(1+x)·50%(1+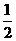 x)=1 320.
x)=1 320.
解得x1=0.2,x2=-3.2(不合题意,舍去).
∴ x=0.2=20%.
 答:新品种花生公顷产量的
答:新品种花生公顷产量的 增长率为20%.
增长率为20%.
反思 (1)当题中牵涉的量较多时, 可通过列表的方式来分析、理解题意.
可通过列表的方式来分析、理解题意.
(2)列方程解应用题时,检验是必不可少的环节,我们需检验两个方面:一是检验未知数的值是否是原方程的解,二是未知数的值是否符合实际意义.
课时训练
8.在实数范围内,方程x2+1=0有解吗?x2-2x+2=0呢?
7.用一根长为24m的绳子围成面积为18m2的矩形,请问这个矩形的长与宽各是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com